住房贷款还款额特性及还款策略研究

郑生钦，王白

(山东建筑大学管理工程学院，山东 济南 250101)

0 引言

越来越多的购房者选择贷款方式买房，但是许多贷款购房者并未考虑过如何合理利用资金，造成了资金浪费和资金利用率低等问题。另一部分贷款购房者虽然意识到了要合理利用资金，提高资金的利用率。但是，他们并不了解还款额中本金与利息的构成方式以及在不同时间还款对利息偿还额的影响，不能在定量分析的基础上进行决策。个人住房贷款的还款策略需要更多的定量分析工具，并经过比较后综合分析来决定的。

国内研究文献[1－2]没有对经过任意还款次数后已偿还利息与还款结束时已偿还利息总额计算方法的研究。而国外研究文献[3－4]对每次还款中所还利息额是如何计算的计算方法缺乏探讨，他们热衷于用还款系数法计算还款额，对用计算器计算还款额有较浓厚的兴趣。由于缺乏对贷款还款特性的系统研究，从而使贷款购房者无法掌握总还款期、利率、已还款期数等因素对利息偿还额、本金偿还额的影响规律，也就无法对不同资金使用方案的代价和收益做出比较，难以制定出适合贷款者的还款策略。

对还款额中的本息构成及变化趋势进行探讨、对使用资金的代价进行定量计算，进而对何时还贷，对提前还贷与购买理财产品、信托产品等资金使用方式下的效率比较等问题进行研究，有助于贷款购房者做出适当的还贷策略，具有研究的必要性。

1 等额本息还款法还款额本金与利息构成

1.1 等额本息还款法简介

根据中国人民银行规定，目前个人住房贷款的偿还方式为:借款期限为1年的，采用到期一次还本付息方式;贷款期限超过1年的，主要采用等额本息还款法和等额本金还款法两种基本的还款方式。等额本息还款法是最为常用的还款方式[1－2]。

尽管影响房地产价格、影响房地产需求的因素有很多[5－6]，但利率和借款资金的使用时间是影响资金使用成本的重要因素，因而也是影响着房地产市场价格的重要因素。

等额本息还款法就是在贷款期限内，每月的还款额是固定的[2]。

每期还款额的计算公式

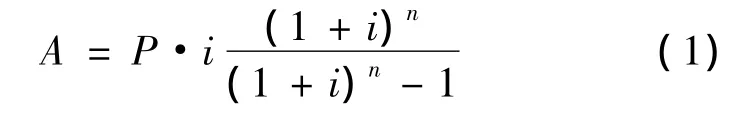
借款本金与每期还款额的关系

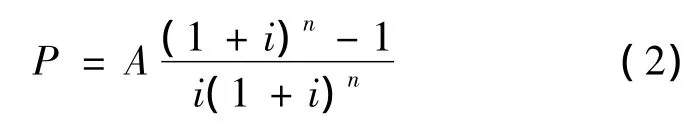
式中:P为贷款总额，元或万元;n为总还款期数，月;i为还款月利率，年利率/12;A为等额本息还款的月还款额，元或万元。

1.2 等额本息还款法还款额中本金及利息的计算

为方便研究，假设后的剩余本金Pt为第t次还款(t=1，2，3，…，n)。

根据上述变量，得到等额本息还款法的现金流量图(如图 1 所示)[2，7]。

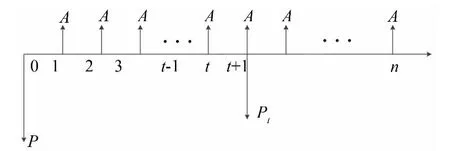
图1 等额本息还款方式现金流量图

第t次的还款额A由本金ACt与利息AIt两部分构成，即

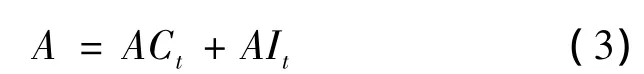
1.2.1 经过t次还款后剩余本金Pt的计算方法

在第t次还款后剩余还款期数为n－t，观察现金流量图(图1)可知，如用n－t替代式(2)中的n，可得第t次还款后剩余本金的计算公式:

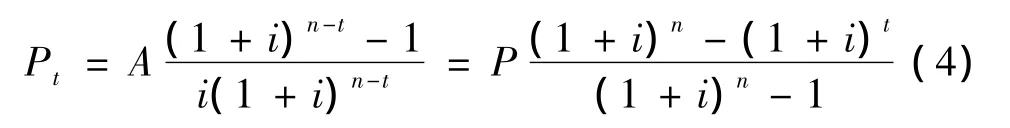
1.2.2 第t次还款额中利息的计算方法

第t次还款的还款额中包括本金和利息两部分。t次还款所还利息是由t－1次还款后的剩余本金产生的。

第t次还款额中的利息为第t－1次还款后的剩余本金Pt－1与相应利率i之积，即

由式(4)知

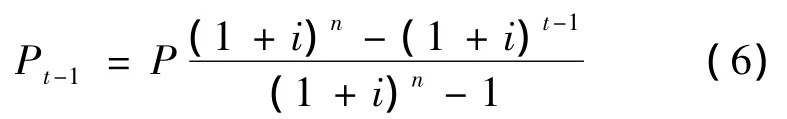
将式(6)代入式(5)求得t次还款额中所还利息为

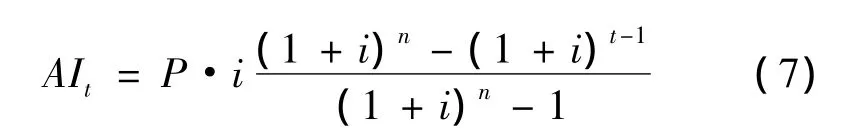
1.2.3 第t次还款额中所还本金的计算方法

由公式(3)得到，每次还款额所还的本金

将式(7)代入式(8)得到第t次还款额中所还本金的计算公式为

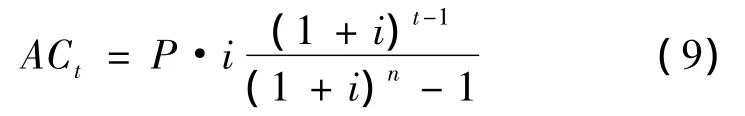
1.3 关于等额本息还款法使用资金的代价

通过对公式(1)、(7)、(8)的观察和继续推导，可以得到一些推论。

1.3.1 等额本息还款法已偿还利息额

假设在第t次还款后已偿还利息额为It，已偿还本息额为F，已偿还本金额为C。

乙组采用DHS内固定术治疗，在股骨粗隆外侧作一长度为12 cm的切口，以便充分暴露近端股骨外侧面。然后，在大粗隆的顶端5 cm位置，经颈干角定位器协助导针前倾15°，置入股骨颈中下方，并将头钉置于股骨颈的中心位置。如果骨折粉碎，则需要通过钢丝/拉力螺钉对骨折块进行固定处理。这时，应在钢板外侧置入螺钉，并将切口缝合，实行负压引流操作。

于是有F=A·t和C=P－Pt，进而有式(10)成立

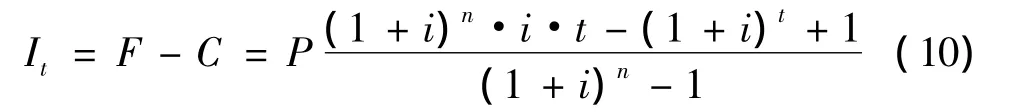
当t=n时，可求得完成还款计划时已偿还利息额，即资金使用的代价

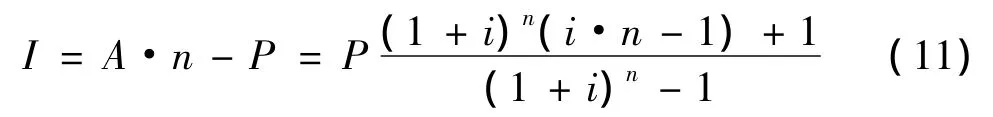
从式(11)中可以看出，在借款本金P与利率i一定的情况下，完成还款计划时的已偿还利息只与总还款次数n有关，即资金的使用时间越长，为使用资金所偿还的利息就越多。

1.3.2 提前还款对利息总额的影响

假设在第m次还款时，除还款额A外，另一次性提前偿还贷款P'元。等价于提前偿还了借款本金P'元，下面探讨因还款计划改变导致的偿还利息额的变化。

剩余还款次数为n－m，因此可用P'替换式(11)中的P，用n－m替换式(11)中的n，求得在剩余的n－m个还款期内的利息额，这就是因提前还款而引起的利息额的减少。

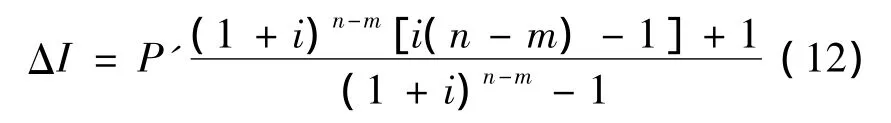
式(12)表明，在总还款期数n一定时，ΔI随m的增大而减小，即还款初期提前还贷可节省更多的利息;在还款期的后期，提前还贷能够节省的利息会大幅度减少。

1.4 还款额中本金与利息随还款次数(时间)的变化趋势

研究还款额A中本金与利息随还款次数的变化趋势，即ACt和AIt随t的变化规律。

等额本息还款法中每次还款额A固定;ACt和AIt因t只能取正整数而不连续，但可以分别看成是连续函数y(t)和z(t)上t取整数时对应值，通过对连续函数y(t)和z(t)变化趋势的研究，得到ACt和AIt的变化趋势。假设

因此，等额本息还款法中第t次还款额中所还本金ACt随着还款次数t的增加而增长，且以增长速率增加;利息部分AIt随还款次数t的增加而减少，并且以递减的速度减少。

1.5 利率对贷款清偿速度的影响

在等额本息还款法下，在第t次还款后，已还本金额

函数y随i的增加而减小，可知等额本息还款方式，在同样贷款期限条件下，经过同样还款次数时，高利率借款的已还本金占借款额的比例，低于低利率的借款的已还本金占借款额的比例，即高利率借款的剩余本金比例高于低利率借款的剩余本金比例。

2 贷款购房案例分析

假设王先生购房时向银行贷款共100万元，采用等额本息还款法进行还款，银行的年利率为6.8%，还款期限为15年，按月还款。

则贷款的本金P=1，000，000元，;还款期数n=15年 ×12期 /年 =180期;年利率i0=6.8%，即计息月利率i=6.8%/12=0.0567%。

2.1 还款额构成变化趋势

将上述参数的值代入公式(3)、(7)、(9)中，A、AIt、ACt看作是以t为自变量的函数，用MATLAB软件作出函数图象(图2)，从图中可以观察到还款额本金利息随还款次数变化的特性。图2表明，随着还款的进行，还款额中本金部分ACt逐渐增加，利息部分AIt逐渐减少，并且有A=ACt+AIt。

2.2 还款额及利息的计算

将上述变量的值代入公式(3)求得，每期的还款额A=8，876.8元;代入公式(11)，可以得到完成还款计划时已还利息额I=597，831元。

2.3 还款额随利率的变化规律

2008年12月27日至今，央行对利率共进行了9次调整，经调整后的住房贷款(5年及5年以上)年利率都在5.94% ～ 7.05% 之间浮动[8]。为方便研究，取年利率从 i0=5.8% 为起始值，以 Δi0=0.25% 为增量，来观察在不同的利率下，月还款额A的变化规律。把变量的值代入公式(1)计算得到在不同年利率下的月还款额(如表1所示)。

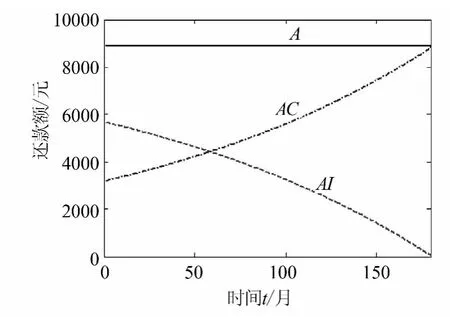
图2 等额本息还款法还款金额构成及变化规律

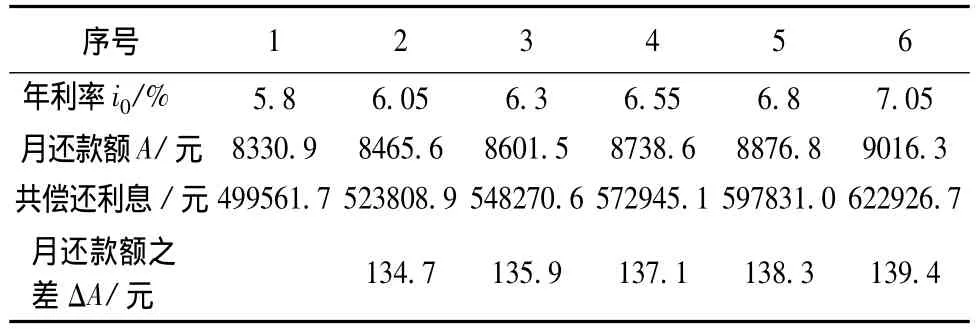
表1 不同利率下的月还款额

我们从表1中可以看出，随着年利率的增长，月还款额也随之增长;并且随着年利率的增长，月还款额之差ΔA也在增长。

2.4 不同还款时段相同还款额中的利息差异

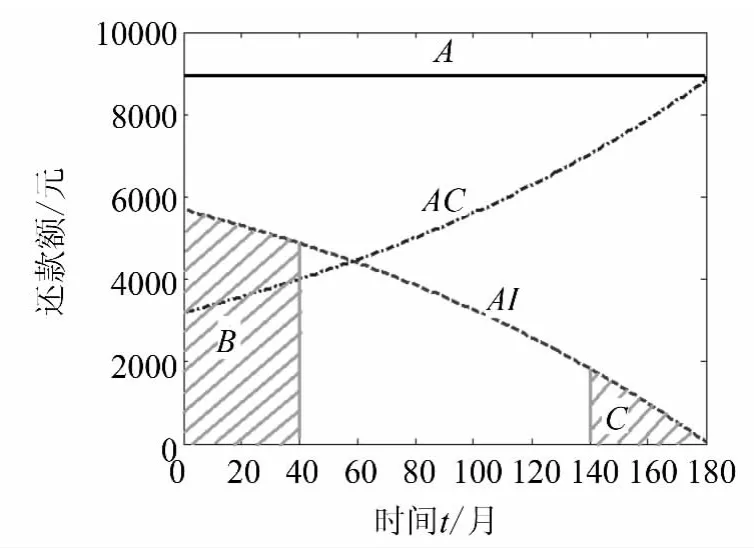
图3 不同还款期还款额中的利息

在图3中可以看出，阴影部分B表示的是还款期限前40个还款期共偿还的利息，阴影部分C表示的是还款期限后40个还款期共偿还的利息。显而易见，还款期限刚开始与还款期限快结束时，虽然每期的还款额是相等的，但是本金和利息的构成却存在着很大的差异。

为了得到利息具体的差异，利用公式(11)与公式(12)进行计算，得到前40个还款期偿还的利息约18.18万元，后40个还款期偿还的利息约4.98万元。虽然都是40个还款期，但是前40个还款期偿还利息是后40个还款期偿还利息的3倍还要多。

因此，在等额本息还款模式下，还款初期还款额中利息占有很大比例，在还款后期利息占有的比例逐渐减少，而本金比例较大。

2.5 在贷款本金和利率固定时，利息总额只与总还款期数有关

从1.3.1中的公式(11)可知，在借款本金P与利率i固定的情况下，还款计划中偿还利息只与总还款期数n有关。

在贷款本金 P=1，000，000，年利率 i0=6.8%，即计息月利率i=6.8%/12=0.0567%的条件下，取还款年限为5、10、15、20、25和30年计算得到在不同还款年限下，需要偿还的利息总额(如表2所示)。可以看出，利息总额随着总还款期数的增加而增加，并且增长速度是递增的。

表2 不同总还款期数利息偿还总额

3 住房贷款的还贷策略研究

购房者面临的客观情况是多样而复杂的，我们在此只分析以下几种情况。在面对其他情况时，也可利用这种思路进行分析。

3.1 提前还贷与按计划还贷之间的选择

购房者在考虑提前还贷时应综合考虑目前及未来的经济状况、已还款期数与未来预期利率等因素。同时，需要在即期消费和延期消费之间做出选择[9]。

在2.4中，我们知道在还款初期和还款后期是所要偿还的利息之间的差额是显著的，因此若是在还款初期还贷，可以少偿还较多利息，提前还贷具有较大意义;但是在还款后期，提前还贷并不能节省很多资金，因此可以选择按计划还贷。

若购房者目前手中资金充裕且在近期没有大额资金或投资支出的情况下，借款人宜考虑提前还贷。

若购房者目前手中资金足够且对未来利率预期是增长的情况下，应该考虑提前还贷。因为在利率增长的情况下，还款额也是随之增长的，并且增长速度随利率增长速度更快。若不提前还贷，将会支付更多的利息。同理，若对未来利率的期望是下降的情况下，可不考虑提前还贷，而是选择消费或其它合适的投资机会。

若购房者目前收入并不可观，并且认为未来收入会增加、经济状况会好转的情况下，即便拥有部分闲置资金，也不必考虑提前还贷。因为目前经济状况下提前还贷会降低购房者的生活品质，而按计划还贷既不会对现在的生活产生影响，也不会对未来的生活水平产生多大的影响。

3.2 还款年限的选择

在2.5中得到这样的结论:利息总额随着总还款期数的增加而增加，并且比还款期数的增长更快。因此在选择住房贷款的还款年限时，若有还款能力，应选择较短的还款年限。

3.3 提前还贷与购买理财产品之间的选择

目前住房贷款的年利率为6.55%，因此实际的年利率。在此以工商银行的理财产品为例进行分析。

2012年11月21日工商银行官方网站显示目前在售的理财产品共5种，其年化收益率因风险与产品期限不同而各不相同。此外，投资者还需要支付给银行0.02% ～0.03%的托管费及0.4%的销售费用。在这5种理财产品中，最高的年化收益率为4.5%，风险等级为 PR3[10]，明显低于住房贷款的实际年利率，并且存在一定的风险，还需支付额外的费用。

除非理财产品的利率达到6.75%以上，才能得出用资金购买理财产品而推迟还贷的结论。即在目前的金融环境下，若购房者有闲置资金，应考虑提前还贷而不是购买银行的理财产品。

3.4 提前还贷与购买信托产品之间的选择

目前的信托产品的年收益率通常都在10%左右，明显高于住房贷款的实际年利率。但是信托产品对购买者有较高的要求，2009年修订的《信托公司集合资金信托计划管理办法》第六条规定，信托产品的购买者应该是能够识别、判断并承担信托计划风险的人。对个人或家庭来说，一个信托计划投入的最低金额不少于100万元、个人或家庭在其认购时有超过100万元的金融资产、最近3年内的个人收入每年超过20万元或者夫妻双方合计收入每年超过30万元。可见，成为信托产品合格投资者的个人或家庭所拥有的资产和年收入要满足规定的要求。

购房者若符合购买信托产品的要求，可以考虑购买信托产品。但是信托产品较理财产品有更大的风险[10]，因此在进行决策时应考虑对风险的承受能力，若购房者认为不能承受与信托产品相应的风险，购房者应提前还贷而不是购买信托产品。此外，由于个人客户资金有限，信托产品门槛较高，只能投资于少量信托产品，风险过于集中，这种情况不利于分散风险[11]。

4 结语

(1)还款额随利率、还款次数、借款期限等参数变化的趋势为:每次还款中所还本金随还款次数的增加而增加，并以递增的速度增加，而每次还款中所还利息额的变化特性则相反。

(2)还款策略为在还款初期或购房者认为未来利率会上涨的情况下，如有还款能力宜提前还贷，反之可按计划还贷;在还款初期提前还贷比在还款后期还贷可节省更多的利息支付。购房者在具有还款能力、并无其他可选投资项目的情况下，宜尽快还款。由于目前理财产品的收益率除低于贷款利率外，有时还要缴纳一些额外费用，因此应选择提前还贷而不宜“有贷不还”去购买理财产品。购房者在符合要求的前提下可购买信托产品而不是提前还贷，但若不能承受与信托产品高收益率相对应的风险，可考虑提前还贷。

(3)几个公式的使用。等额本息还款法是中国商业银行普遍采用的住房抵押贷款还款方式。通过初始借款额、借款期限、已还款次数、贷款利率四个参数利用文中推导的公式(4)可以直接计算住房贷款的借款余额。在此基础上推导出来的计算每次还款额中所还利息的公式(7)和计算所还本金的公式(9)、以及计算已偿还利息的公式(10)也都只含有这四个参数。这些公式可以直接计算第t次还款中的利息、本金，经过第t次还款后的已偿还利息，并为讨论本金、利息、已偿还利息、使用资金代价等还款变量随四个参数的变化趋势提供了可能，对于还款决策具有一定的理论价值和实践价值。

(4)今后研究方向。可以针对还款特性、信托和理财等产品的收益与风险、还款策略等因素构建系统决策模型，进行系统的研究，为购房贷款者的还贷决策提供系统评估，更好地满足抵押贷款购房者是提前还款还是投资理财、信托的决策需求。

[1]张红，殷红.房地产金融学[M].北京:清华大学出版社，2006.

[2]刘洪玉.房地产开发经营与管理[M].北京:中国建筑工业出版社，2011.

[3]布鲁格曼，费雪.房地产金融与投资[M].李秉祥，孙鸿飞，钱勇译(第十版)，大连:东北财经大学出版社，2000.

[4]克劳瑞特，西蒙.房地产金融:原理与实践[M].龙奋杰，李文诞译(第三版).北京:经济科学出版社，2004.

[5]高健，周丽萍，王文科，等.主成分分析法在住宅特征价格模型中的应用[J].山东建筑大学学报，2008，23(1):15 －19.

[6]邓庆旦，马振伟，王飞，等.济南市保障性住房制度建设的问题与对策[J].山东建筑大学学报，2011，26(3):204－208.

[7]Lasher W.R ..Practical Financial Management[M].South-Western，Cengage Learning，2008..

[8]中国人民银行.金融机构人民币贷款基准利率.[EB/OL].http://www.pbc.gov.cn/publish/zhengcehuobisi/631/2012/20120706181352694274852/20120706181352694274852_.html，2012－07－06.

[9]Horne J.C.，Wachowicz J.M..财务管理基础[M].刘曙光 译.北京:清华大学出版社，2006.

[10]中国工商银行.中国工商银行“安享回报”黄金套利投资型人民币理财产品说明书.[EB/OL].http://www.icbc.com.cn/icbc/%e7%bd%91%e4%b8%8a%e7%90%86%e8%b4%a2/%e7%90%86%e8%b4%a2%e4%ba%a7%e5%93%81/%e4%ba%a7%e5%93%81%e9%a2%84%e8%a7%88.htm?addStr=AXTL1205/ProductIntro/AXTL1205ProductIntro.html＆productId=AXTL1205＆buyflag=3，2012 －11 －21.

[11]哈尔·R.范里安.微观经济学:现代观点[M].费方域，译.上海:机格致出版社，2011.