大型管件管端过弯矫圆控制策略研究

展培培 赵 军 尚京华 马 瑞

燕山大学，秦皇岛，066004

0 引言

目前，油气输送管道作为一种经济、安全的输送工具得到了迅速发展［1］。大口径直缝埋弧焊管（LSAW）因具有优异的焊缝质量，正在逐步取代螺旋缝焊管（SSAW），并在管线钢管产品中起主导作用。椭圆度是衡量LSAW管件的标准之一。美国制管协会 API Spec 5L标准［2］规定，管体椭圆度不应超过钢管公称直径的1.0%，而对于管端，若其椭圆度超过标准范围，将直接导致管端焊接坡口车削加工困难，使其尺寸不达标，进而限制其具体使用过程中管件间的焊接连接工艺，造成管件焊后残余应力过大，影响焊缝寿命，因此管端椭圆度要求较管体椭圆度要求更为严格。

相关研究表明，LSAW管件生产过程中的扩径工序对管件整体的椭圆度有一定的矫正作用［3－4］，但是不可避免地仍有部分管件在扩径后由于热处理变形、残余应力的释放以及放置过程中的蠕变等因素的影响而造成管端的椭圆度不达标，因此需进行矫圆处理。由于扩径在矫圆的同时会改变管坯的周长尺寸，因此不再适用。简单、经济且最有效的方法就是用一对小曲率圆弧瓣模压制管坯端部，使其产生塑性变形，从而减小椭圆度误差（简称为管端过弯矫圆）。目前，生产厂家主要依赖操作者的经验反复测量，反复压制管坯来减小椭圆度误差，生产效率低下，因此厂家急需合理的管端矫圆控制策略。

由管端过弯矫圆的工艺特点可知，管端矫圆过程塑性变形区主要集中在管坯端部一小段区域内，未变形区的刚端牵连对矫圆过程产生很大影响，因此，单纯从理论上分析其变形过程，并给出合适的矫圆工艺参数存在一定困难。有限元方法虽然能解决该问题，但是需耗费较长的时间。若忽略管端矫圆过程中的刚端影响因素，只考虑主变形区的变形特点，则可以将其近似为平面应变问题。无论是采用理论解析法还是有限元分析方法，都能在较短的时间内给出平面问题的变形规律。

本文首先通过物理实验研究扁矫圆与圆压扁之间的等价关系，以及管端压扁与短管整体压扁之间的相似性关系，进而结合基于平面应变的管坯压扁过程的数值模拟给出管端过弯矫圆两步法控制策略。

1 管端过弯矫圆概述

管端过弯矫圆是一种基于纯弯曲的矫圆工艺，矫圆前后被矫对象截面周长近似不变。由圣维南原理可知，管坯沿其轴向方向可分为与模具接触的管端主变形区、受变形影响的牵连变形区以及未变形区三个主要区域。其中，主变形区长度用L表示。

管坯端部主变形区的变形过程示意图见图1。变形过程中，A点及其邻近区域中性层曲率不断减小，产生反向弯曲，B点及其邻近区域中性层曲率不断增大，产生同向弯曲。考虑到弯曲回弹的影响，初始纵向椭圆只有矫至横向椭圆，卸载后管坯截面才能成为圆形。

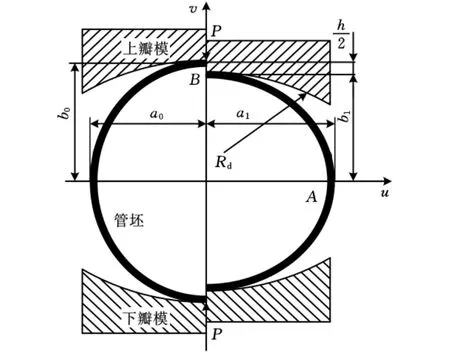
图1 管端模压式过弯矫圆示意图

2 过弯矫圆等价关系

为降低分析难度，首先通过实验方法分析待矫圆管坯的矫圆过程与圆截面管坯压扁过程，确定两个成形过程的工艺参数与卸载后椭圆度之间的关系，进而寻求将压扁过程的规律用于过弯矫圆过程中的可能性。

实验在WDD－LCT－150型电子拉扭组合多功能实验机上完成，位移控制精度为0.01mm。管坯的测量采用便携式三坐标测量仪完成，其测量精度为0.01mm。管坯试件几何尺寸如表1所示。实验模具模腔截面圆弧半径为120mm。在长管坯管端变形过程中，为减小矫圆瓣模端部附近管坯的应力集中，瓣模的一端被加工成锥角为7°、长度为20mm的倒角。实验装置见图2。

表1 管坯试样几何参数

图2 过弯矫圆实验装置

分别以长管坯和短管坯为研究对象，制订实验方案如下：第一步，圆截面管坯模压压扁过程，以确定的压下量h和主变形区长度L将长管坯端部或整体短管坯压成椭圆，记录卸载后的管坯椭圆度；第二步，管坯矫圆过程，将第一步卸载弹复后具有一定椭圆度的管坯绕其轴线旋转90°，并以与第一步相同的实验装置，相同的方式和相同的压下量压制管坯，记录管坯最后的残余椭圆度。

椭圆度δ［2］的定义为

式中，a、b分别为图1所示的管端以外表层度量的u方向半轴和v方向半轴；D为管坯的公称外径。

不同压下量、不同变形区长度条件下的实验结果如表2所示。表中，L在管端变形时表示主变形区长度，在短管变形时表示管长。相对压下量H的定义为

由实验结果可知，管坯残余椭圆度最大为0.31%，最小为0.19%，都远小于管线钢管残余椭圆度1%的要求，且残余椭圆度均为正值，表明用同一管坯完成两个变形过程实验时，管坯材料的包辛格效应是导致残余椭圆度的主要原因。

表2 过弯矫圆等价关系实验结果

实验结果表明：在工程应用的精度范围内，矫圆过程等价于压扁过程，所谓等价是指可以将圆截面管坯经模压方式压成待矫圆管坯椭圆度所需的压下量作为过弯矫圆的压下量对待矫圆管坯进行矫圆处理。

3 刚端影响相似关系

以相同材质、相同规格的圆截面长管坯和短管坯为研究对象，以一定的主变形区长度和压下量使长管管端被压扁，短管整体被压扁，记录力与行程曲线及卸载后的椭圆度，研究两者之间的变形相似性规律。实验装置和长管坯规格与上述等价原理中相同。

以表1所示外径为76.2mm的管坯为实验对象，实验装置与上述等价关系中实验装置相同，分析管坯在压扁过程中的刚端影响相似关系。

压下量为3mm时，管坯卸载后椭圆度随管端压扁过程中的主变形区长度L以及短管整体压扁过程中的短管长度的变化关系曲线如图3所示。随着主变形区长度的增大，管端卸载后椭圆度也逐渐增大，这是由于在变形量较小条件下，长管管端受刚端影响较大，弯曲后回弹量较大，导致最终椭圆度偏小。而短管变形后椭圆度在一小范围内波动，即管坯长度对变形后椭圆度的影响不大。

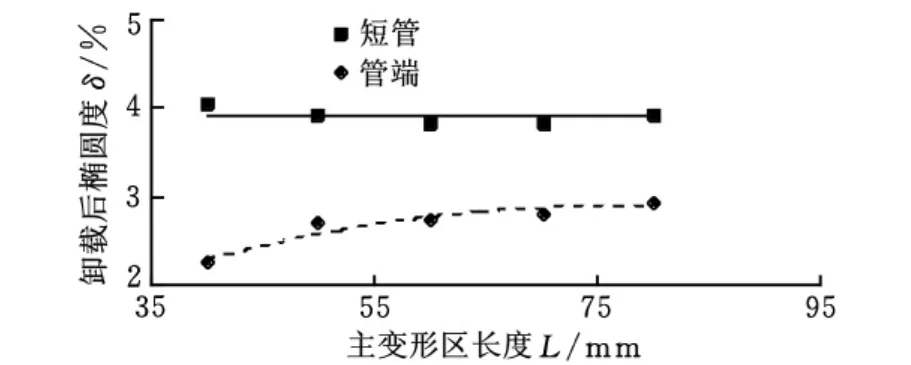
图3 卸载后椭圆度随主变形区长度变化关系曲线

管长为60mm的短管坯整体压扁与主变形区长度L为60mm的长管坯端部压扁过程的实验中，力与行程曲线如图4所示。压下量较小时，管坯均产生弹性变形，载荷相差不大，进入塑性变形阶段后，长管管端模压压扁过程所需载荷的上升速率明显大于短管坯。短管坯的最大载荷为9.5k N，载荷与管壁截面面积比值为管壁截面的最大正应力值，为19.8MPa，相对于20钢的屈服极限较小。由此可以证明截面弯矩是引起管坯塑性变形的主要原因。

图4 有无刚端影响时的力行程曲线

主变形区长度分别为40mm和60mm的长管坯管端压扁过程和长度为60mm的短管坯压扁过程中，管端卸载后椭圆度与相对压下量之间的关系曲线如图5所示。

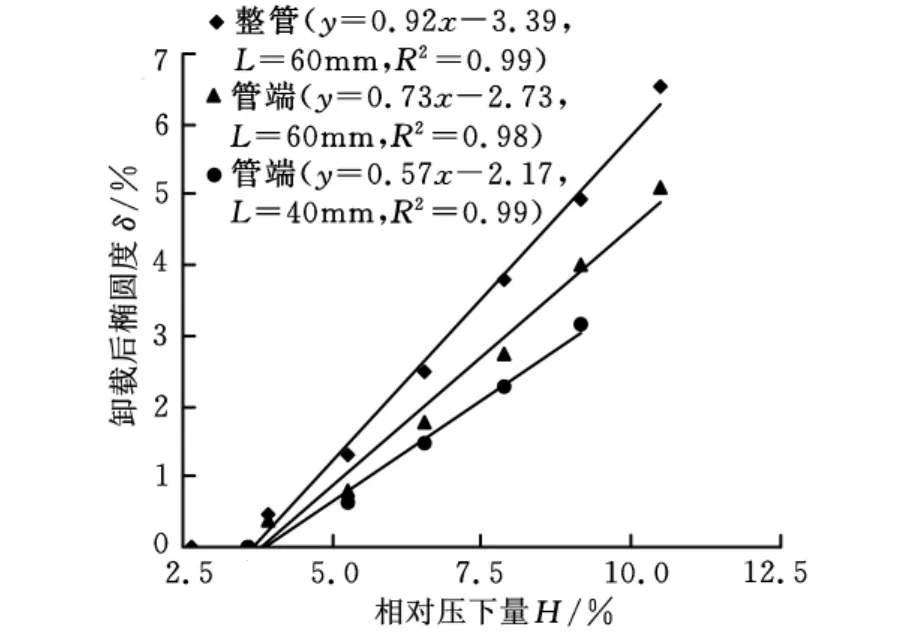
图5 卸载后椭圆度与相对压下量关系曲线

由图5可知，两种变形方式下，曲线的变化趋势相同。相对压下量较小时，管坯均处于弹性变形范围内，卸载后管坯椭圆度不变，而随着相对压下量的逐渐增大，两种管坯卸载后椭圆度均随相对压下量的增大而近似线性递增。线性拟合塑性阶段的相对压下量与卸载后椭圆度实验数据，其线性拟合的相关系数R2值均大于0.98，非常接近1。由此可表明在工程允许的精度范围内完全可以使用线性关系来确定过弯矫圆的工艺参数。

根据上述实验数据的拟合直线结果可知，三条直线方程的横轴截距分别为3.68、3.72和3.80，三者之间相差较小，在工程误差许可的范围内，可近似认为其相等。

比较上述主变形区长度不同的长管坯压扁结果可知，变形区长度为40mm时的相对压下量与卸载后椭圆度之间线性关系中的斜率明显小于变形区长度为60mm时的斜率，即随着变形区长度的增大，其线性关系的斜率也逐步增大，直至变形区长度无限大以致可以忽略刚端的影响时，其斜率与无刚端影响时相同。

4 短管整体压扁过程数值模拟分析

由图3可知，管件的长度对短管整体压扁过程影响相对较小，即变形过程可近似为平面应变。根据对称性，选取四分之一管截面为数值模拟分析对象。模具选用刚性体。管坯规格与表1所示外径为76.2mm的管坯相同，管坯材料性能通过单向拉伸实验获得，拉伸试样通过纵向切取管壁制备，拉伸实验结果如图6所示，其中，材料弹性模量E＝206GPa，屈服强度σs＝302MPa。有限元分析软件选用ABAQUS，分析步选用准静态，网格单元选用CPE4R（四节点平面应变一阶减缩积分）单元。管壁厚度方向划分为7层，总体共392个单元。四分之一管截面两端分别施加对称约束。

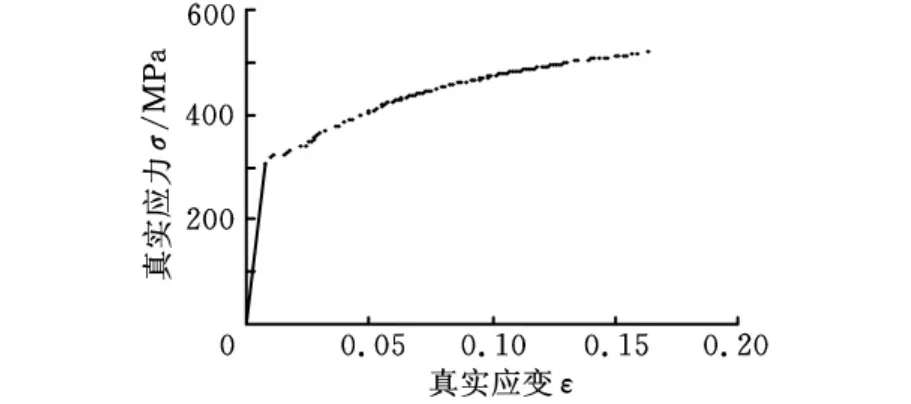
图6 管坯材料拉伸实验真实应力应变关系曲线

管坯加载后的Mises等效应力云图见图7，沿管壁厚度方向的应力分布出现明显的分层现象，即外表层应力比中性层应力大，该应力分布状态为典型的弯曲应力分布。另一方面，管坯竖直方向压点附近的应力最大值较水平方向的应力最大值大，说明变形过程中压点附近最先达到塑性屈服。

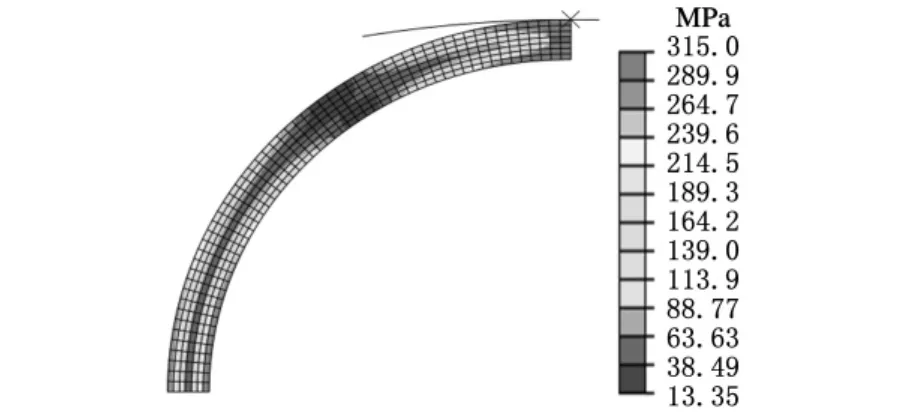
图7 管坯加载后等效应力云图

根据数值模拟分析，卸载后椭圆度随相对压下量的变化曲线如图8所示。图中实验点与图5中相同，细实线为数值模拟结果。数值模拟结果与实验点之间误差较小，根据线性拟合模拟结果的塑性阶段实验数据可得到其线性关系的横轴截距为3.71，与图5中数据拟合结果相差较小，可近似认为其相等。

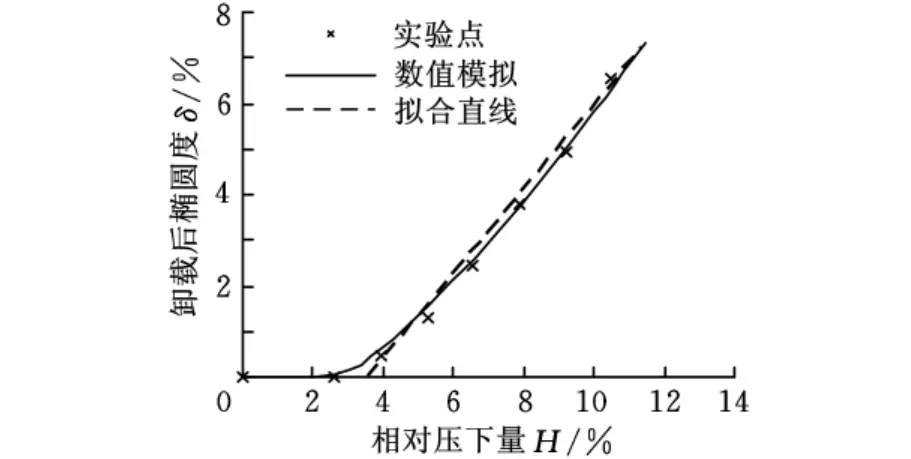
图8 模拟结果与实验结果对比曲线

5 管端过弯矫圆两步法控制策略

由于材料性能的波动，通过理论模型准确地预测每一个管坯的矫圆压下量存在一定的困难，因此，选择合理的控制策略具有很大的实际应用价值。两步法控制策略示意图见图9。

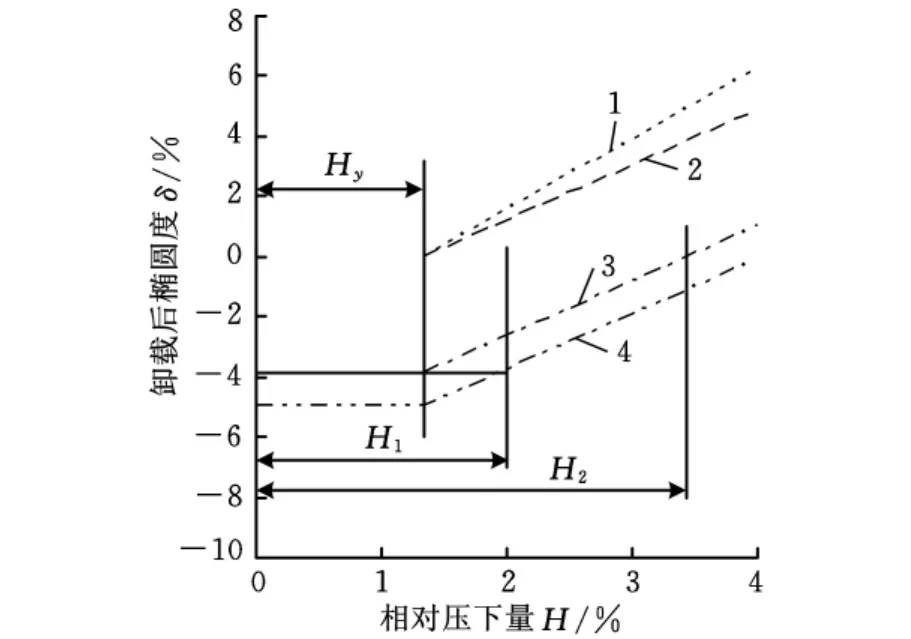
图9 两步法控制策略示意图

根据上述过弯矫圆等价关系可以推得直线2、3、4的斜率与起始点横坐标相等；再根据管端压扁过程与短管整体压扁过程相似关系可知，两者线性关系的起始点横坐标相同，且等于短管整体压扁过程中线性关系的横轴截距Hy。

由此可建立管端矫圆两步法控制策略，即对某一初始椭圆度为δ0的管端待矫圆长管坯进行两次施压以矫正其椭圆度。第一步，以一定压下量H1预压管坯端部，使其产生塑性变形，记录卸载后管端椭圆度δ1。第二步，利用已知直线1和图9所示关系计算得到二次矫圆相对压下量H2，并对管坯进行第二次压制，完成矫圆过程。

H2的计算方法如下：令直线1的方程为

式中，F′、G′分别为其线性关系中的斜率与截距。

由该线性关系得

设直线2的方程为

同样，F0、G0分别为其线性关系中的斜率与截距。直线3的方程为

其中，G1为其线性关系的截距。该线性关系的起始点坐标为（Hy，δ0），根据上述第一步压制结果，（H1，δ1）同样为该直线方程中坐标，其中H1为管坯预压的相对压下量。由此，可以解得

初压后待矫圆管坯的残余椭圆度为δ1，即直线4方程为

式中，G2同样为此线性关系的截距。

该线性关系的起始点坐标为（Hy，δ1），斜率为F0，将式（7）代入式（8）即可解得G2，进而求得当式（8）中卸载后椭圆度δ＝0时的相对压下量，即管坯第二步加载时所需相对压下量：

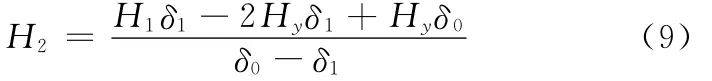
式（9）中，Hy通过对压扁过程进行数值模拟，分析其变形规律获得。

6 控制策略验证实验

选取4个初始椭圆度不同的长管坯对上述的管端过弯矫圆两步法控制策略进行验证，结果如表3所示。长管坯规格与表1所示长管坯相同，主变形区长度L为60mm。初始椭圆度长管坯通过径向施压方式制取。控制策略用到的Hy值采用图8所示的数值模拟结果，并且管端矫圆过程中的第一步相对压下量统一采用约1.5倍的Hy，即为5.25mm。

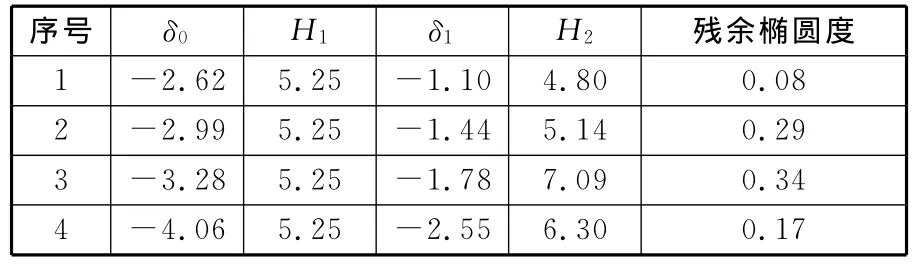
表3 过弯矫圆控制策略实验结果 %

由实验结果可知，4个管坯残余椭圆度最大值为0.34%，最小为0.08%，最终结果仍在一小范围内波动，表明矫圆策略中的相似关系和管坯材料性能的波动对管坯最终的矫圆质量有一定影响，但是最终结果均很大程度上满足了管件标准的要求。

7 结论

（1）扁矫圆与圆压扁两个过程之间存在等价关系。所谓等价，是指在工程应用的精度范围内，可以用圆截面管坯经模压方式压成待矫圆管坯椭圆度所需的压下量作为过弯矫圆的压下量对待矫圆管坯进行矫圆处理。

（2）圆截面长管坯管端压扁过程与短管坯整体压扁过程之间存在相似关系。所谓相似是指，两个过程中塑性变形阶段卸载后椭圆度与相对压下量之间均为近似线性关系，且其线性关系的横轴截距相等。随着主变形区长度的增大，管端圆压扁直线的斜率增大，最终与整管压扁的直线斜率趋于一致。

（3）通过结合物理实验和模拟分析给出了管端过弯矫圆两步法控制策略，实验验证表明，根据上述结论建立的管端矫圆两步法控制策略可以将残余椭圆度控制在0.5%以内。

［1］杨秀琴.我国钢管工业的现状、问题与发展前景（上）［J］.钢管，2008，37（1）：12－17.

Yang Xiuqin.Current Situation Existing Problems and Development Prospect of Domestic Steel Tube Industry（PartⅠ）［J］.Steel Pipe，2008，37（1）：12－17.

［2］ANSI/API Specification 5L.ISO 3183－2007 Specification for Line Pipe［S］.Washington DC：API Publishing Service，2009.

［3］郭宝锋，金淼，吴生富，等.扩径率和重叠量对机械扩径制品品质的影响［J］.中国机械工程，2004，15（12）：1111－1114.

Guo Baofeng，Jin Miao，Wu Shengfu，et al.Influences of Expanding－ratio and Overlap－length on the Quality of Finished Products［J］.China Mechanical Engineering，2004，15（12）：1111－1114.

［4］殷璟，赵军，屈晓阳.大型管件扩径矫圆弹复分析［J］.机械工程学报，2011，47（12）：32－42.

Yin Jing，Zhao Jun，Qu Xiaoyang.Springback Analysis of Expanding and Setting Round for Large Diameter Pipe［J］.Chinese Journal of Mechanical Engineering，2011，47（12）：32－42.