透镜式薄壁CFRP管压扁力分析
2017-06-15高冀峰胡建辉陈务军陆邵明房光强彭福军
高冀峰,胡建辉,陈务军,陆邵明,房光强,彭福军
(1. 上海交通大学空间结构研究中心,上海 200240;2. 上海交通大学船舶海洋与建筑工程学院,上海 200240;3. 上海宇航系统工程研究所,上海 201108)
透镜式薄壁CFRP管压扁力分析
高冀峰1,胡建辉1,陈务军1,陆邵明2,房光强3,彭福军3
(1. 上海交通大学空间结构研究中心,上海 200240;2. 上海交通大学船舶海洋与建筑工程学院,上海 200240;3. 上海宇航系统工程研究所,上海 201108)
针对透镜式薄壁纤维增强聚合物(CFRP)管伸展臂在截面设计中需确定压扁力的问题,选取两种不同截面、长度、铺层和材料参数的薄壁CFRP管,通过试验和数值模拟分析其压扁过程中的压扁力和截面变化特征。压扁过程中,假设截面不存在局部接触变形,且是线性等曲率变化,建立压扁力近似算法1;假设给出截面局部接触变形函数,建立压扁力近似算法2。综合试验、数值模拟与两种近似算法的结果,发现压扁过程中压扁力与截面变形均表现出较强的非线性特性,可用近似算法2估算压扁力。
透镜式薄壁管;CFRP复合材料;试验研究;数值模拟;近似算法;压扁力
0 引 言
透镜式薄壁纤维增强聚合物(Carbon fiber reinforced polymer,CFRP)管作为一种空间支撑结构,具有材料高比强、韧性好、热膨胀系数小等优点。其由上下两近似“Ω”型薄壳结构粘合而成,利用薄壳弹性变形可实现展开与折叠。展开后的稳定工作状态为透镜形,收拢时由压扁机构施加管片压扁力,绕中心弯曲实现缠绕收拢。可作为空间收展航天器如太阳帆、空间薄膜天线阵面等的支撑体系构件,美、德等西方多国已较早开展相关研究与应用[1-5]。围绕其自身结构性能与收展过程中的力学机理,已吸引国内外众多机构的研究人员做相关研究。
在静力、动力和稳定特性方面,李瑞雄等[6]和蔡祈耀等[7]、Hu等[8]、Sickinger等[2]选取不同材料、截面参数的薄壁CFRP管进行试验和数值模拟,研究了薄壁管的自振模态和轴压、弯曲屈曲承载力。Irwin等[9]通过四点弯曲试验,分析并计算了薄壁管的弯曲刚度和承载力。
在收展过程中的力学机理方面,丁峻宏等[10]利用显式动态算法和高性能计算资源,对薄壁管盘卷收拢和展开过程进行了非线性准静态仿真。李瑞雄等[11]与蔡祈耀等[12]采用试验、数值模拟分析了薄壁管缠绕压扁过程中的受力特性,但研究缺少相应的理论分析。Chu等[13]与Hakkak等[14]根据各向同性材料小应变弹性假设,建立了薄壁管在压扁状态的应变能与最大应力计算公式。
上述分析主要侧重研究薄壁管自身的力学特性,薄壁管作为伸展机构的一部分,其缠绕收拢时所需的压扁力是薄壁管截面、压扁驱动机构设计中需要考虑的重要因素之一,但鲜有研究涉及。Bai等[15]在管壁小应变平截面变形假设的基础上推导了CFRP管压扁力的理论公式,缺少结合变形考虑压扁过程中几何、接触非线性特性。因此有必要从薄壁管压扁过程中的变形特征出发,深入分析其压扁过程中的受力特性,并尝试给出估算压扁力的近似方法。会有助于在多种截面、材料及铺层组合方式下的试算选型,提高设计效率。
本文首先应用试验、数值模拟,研究了长度为5cm、20cm的两种不同截面尺寸、铺层及材料参数的薄壁CFRP管在压扁过程中压扁力和截面的变化特征。然后假设截面不存在局部接触变形,且是线性等曲率变化,建立了压扁力近似算法1;假设给出截面局部接触变形函数,建立了压扁力近似算法2。最后综合分析试验、数值模拟和近似算法的结果并做出总结。
1 试 验
试验分析薄壁管压扁过程,可较真实地研究其非线性行为和力学特征。选取两种常用薄壁管截面CS1、CS2如图1~2所示,以x、y轴为对称轴。图3为CS2截面管压扁试验过程图。材料参数、铺层方式及壁管长度如表1所示,铺层0°方向对应图4中z向。

表1 管片复合材料参数Table 1 Composite laminate material parameters

表2 压扁试验加载法则Table 2 Loading rules for flattening test
试验加载设备采用Zwick/Roell Z010测试系统,力传感器量程为1000N,测量精度为最大试验力的0.5%。对CS1、CS2截面薄壁管各三组试件加载压扁,试验装置如图3所示,试验过程如下:
1) 试验开始前保持管段水平,将下部薄壁管圆弧段中点处与试验台钢板粘结,以使管段能够平稳压扁。
2) 下移加载板使之与管段刚好接触,对试验机设置接触反力,之后同时记录加载力与下压位移值。
3) 试验采用等速率分步位移加载,每步加载速度均为10mm/min,并且各加载步之间设置固定的保载时间。为防止压扁后挤压到应变片和数据线,试验压扁结束时留有3~5mm间隙,CS1、CS2截面试件的总下压位移分别为65mm、115mm,加载法则见表2。
2 数值模拟
应用Abaqus/Standard有限元软件按图2尺寸建立分析模型,因截面关于x轴对称,只建立x轴上半部分模型如图4所示,材料截面铺层(ply)如图5所示。铺层复合材料每层设置3个积分点,压板与薄壁管采用主从接触,不考虑摩擦。两侧水平翼板与下部刚板间设置间隙以模拟粘结处的双层厚度,间隙距离同壁厚。上、下刚板采用解析刚体单元,管壁采用考虑剪切变形的通用壳单元S4R,CS1、CS2模型总单元数目分别为8200、14100。考虑到压扁过程中上下管壁为对称变形,及两侧水平翼板的粘结约束作用,边界条件设置见表3。
薄壁管压扁过程模拟,是考虑接触及几何非线性下的弹性变形分析,并不涉及材料屈曲。采用静态通用分析步并打开几何非线性分析(Nlgeom ON),上刚板采用位移加载,设置初始步长0.01,最大步长为0.05。两种薄壁管建模方法相同。

表3 边界条件Table 3 Boundary conditions
数值模拟结果中,CS1、CS2截面薄壁管表现出了相似的变形、接触特征。因较长的CS2截面管更具有一般性,对其变形做进一步分析。图6、7分别给出了CS2截面薄壁管下压115mm时,上表面的最大、最小主应变云图及方向指示。箭头指向外部代表拉应变,指向内部代表压应变。箭头的相对长度代表其起始处积分点的主应变值,软件中设置了较小的显示密度以达到清晰的效果,箭头分布位置由软件随机选取。
当薄壁管接近压扁时,由图6可知,左右两侧圆弧出现整体坐标x方向的主拉应变;中间圆弧除两侧自由边附近外,最大主应变均为负值,为受压区域。由图7可知,中间圆弧出现x方向的主压应变;两侧圆弧最小主应变依然为正值,均为受拉区域。文献[13-14]假设薄壁管压扁过程为单向弯曲变形,给出了计算截面压扁后应变绝对值的近似公式:
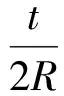
(1)
式中:t为薄壁管壁厚,R为初始半径。由式(1)计算CS2截面应变值为3×10-3,接近图6左右圆弧的最大主应变和图7中间圆弧的最小主应变值。截面反弯点为拉、压应变的分界点,应变绝对值较小。
综合主应变分析结果可发现,薄壁管截面压扁过程中呈现出明显的单向弯曲变形特征,因此可以将模型做单向变形简化,分析压扁力的变化特征。
进一步分析压扁过程中的接触现象。图8为压扁过程中,由软件读取结点相关接触面积(Contact area associated with each node in contact,CNAREA)变化云图,其数值近似反映了单元的接触面积,可作为分析参考。因建立CS1、CS2截面薄壁管模型单元边长分别为1mm、2mm,所以图8中接触面积参数最大值分别接近10-6m2和4×10-6m2。图中深色区域是接触位置,管壁两侧水平翼板因设置间隙,不显示接触。
结合图2和图8可知,压扁过程中薄壁管截面形状不是线性等曲率变化。中间、两侧曲率变化最大,至反弯点处曲率变化最小。压板与管壁的接触位置、面积也不是均匀渐变过程,由初始的接触线扩展为接触面,管壁中间圆弧出现局部反向弯曲,如图8(a)、8(c)所示。接触面自中间、两侧逐渐向反弯点处扩展,如图8(b)、8(d)所示。在扩展过程中呈现出不规则变化,表现出较强的非线性特征,试验过程中也发现了上述变形、接触现象。
3 近似算法
由数值模拟压扁过程(图8)可知,压扁过程中薄壁管截面及接触面变形复杂,不易建立理论解析式,本文尝试采用两种不同的变形假设,分别给出计算压扁力的近似算法,并比较其计算效果。
首先两种近似算法做相同简化:压扁过程简化为铺层复合材料薄壳的单向弹性弯曲变形,且不考虑横向变形、受力耦合效应。
在上述简化为单向弯曲变形的前提下,可根据铺层复合材料理论计算CS1、CS2薄壁管弯曲刚度,有如下计算式[16]:
(2)
式中:n为铺层数目,hk为厚度方向各层距中性面的距离,Q为各层折减转换刚度系数,D为弯曲刚度。经计算,长度分别为50mm、200mm两种薄壁管截面CS1、CS2弯曲刚度分别为0.203N·m2、0.098N·m2。
3.1 近似算法1
图9为近似算法1的1/4管截面计算简图,假设压扁过程中不存在局部接触变形,管壁始终受两个集中荷载,在高度方向以反弯点处的水平弦长L为轴线对称变形,并且截面为线性等曲率变化。可建立截面变形的几何关系式(3)~(5):
(3)
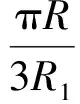
(4)
L=R1sinθ
(5)
式中:R为初始半径,R1为挤压变形后半径,h∈[0,2R]为总挤压距离,L为水平弦长,为原π/3弧长在压扁过程中对应的新弧度值。通过式(3)~(5)即可由挤压距离h确定变形后半径R1与水平弦长L。
根据曲率变化,可求得简图中两端弯矩M如式(6)所示,并根据弯矩平衡求得1/4管截面的压扁力F如式(7)所示。
(6)
(7)
综合式(3)~(7)可建立近似算法1,求得压扁过程中下压距离h与总压扁力2F的对应关系。
3.2 近似算法2
图10为近似算法2的1/4管截面计算简图。由有限元接触面积(图8)可知,压扁过程中薄壁管的接触面不是平面,面上不是均布荷载,存在局部下凹,试验过程中也发现了此现象。因压扁过程中横截面、接触面与下压距离的关系无法准确描述,所以结合有限元结果做出如下假设:
1) 压扁过程中1/4管截面反弯点两侧变形相同,剩余弧度与总挤压距离h∈[0,2R]存在关系式(8),其中指数0.7为调整系数。
2) 力作用在局部压扁面边缘,考虑到真实接触力并非是端部的集中力,力臂没有取集中力间的垂直距离,按图中2L即式(9)计算。
3) 刚板与管壁接触产生的局部压扁是渐变出现的过程,引入水平压扁长度比值S/S1作为端部弯矩折减系数,即端弯矩按式(10)计算。
(8)
2L=2×R×sinθ
(9)

(10)
将式(8)~(10)代入弯矩平衡方程M=FL,可求得1/4管截面挤压力F如式(11)所示。

(11)
综合式(8)~(11)可建立近似算法2,同样求得压扁过程中下压距离h与总压扁力2F的对应关系。
4 结果对比
CS1、CS2截面薄壁管试验、数值模拟及近似算法的压扁结果如图11~12所示。
由图11~12可知,前期压扁力与变形接近线性变化关系,此时薄壁管较容易压扁,之后压扁力迅速增大而变形增加缓慢,压扁力与变形呈非线性变化关系。CS1、CS2截面薄壁管达到最大压扁位置65mm、115mm时的压扁力分别为68.3N、98.6N。CS1薄壁管压扁过程出现非线性变化的临界位移为53mm、平均临界压扁力为23.6N,分别为总截面高度的77.9%、最大压扁力的34.6%;CS2截面薄壁管临界位移为100mm、平均临界压扁力为31.7N,分别为总截面高度的83.3%、最大压扁力的32.2%。图11中CS1截面薄壁管试验结果离散性较大,是首批试件材料、制备方法不稳定所致。
由近似算法结果可知,近似算法1计算压扁力接近线性变化,两种截面薄壁管计算结果均小于试验值与数值模拟结果。说明截面存在接触变形,且不是线性等曲率变化。
近似算法2基本能反映出压扁力变化的整体趋势,对不同截面薄壁管,计算结果略有差异。计算CS1截面薄壁管,压扁力68.3N对应的下压位移为61.2mm,位移误差为5.8%。计算材料特性与制备较稳定的CS2薄壁管,压扁力98.6N对应的下压位移为112.8mm,位移误差为1.9%。主要参考近似算法2与较长的CS2薄壁管压扁试验结果,在截面选型试算时,可取截面总高度的95%作为计算位移,估算总压扁力。
5 结 论
本文选取两种不同截面、长度、铺层和材料参数的薄壁CFRP管,通过试验和数值模拟分析了压扁过程中压扁力和管截面的变形特征。基于两种变形假设,分别建立了计算压扁力的近似算法,综合试验、数值模拟和近似算法的结果,得到以下结论:
1)可将压扁过程简化为单向弯曲变形。前期压扁力与压扁位移呈近似线性关系,当压扁位移接近总截面高度的80%时,压扁力仅为总压扁力的35%左右,之后压扁力迅速增大而变形增加缓慢,管截面及压扁机构设计时需考虑此现象。
2) 近似算法1计算压扁力结果较小。压扁过程中,管截面不是线性等曲率变形,中间、两侧曲率变化最大,反弯点处最小;管壁存在因接触产生的局部压扁,并由中间、两侧向反弯点处扩展。截面变形表现出较强的非线性特征。
3) 近似算法2假设变形函数计算压扁力,基本能反映出薄壁管压扁力的变化趋势。在CS1、CS2两薄壁管试验中,计算最大压扁力,位移误差分别为5.8%、1.9%。在构件截面选型试算阶段,可取总截面高度的95%作为计算位移,估算总压扁力。
[1] Puig L, Barton A, Rando N. A review on large deployable structures for astrophysics missions[J]. Acta Astronautica, 2010, 67(1): 12-26.
[2] Sickinger C, Herbeck L, Breitbach E. Structural engineering on deployable CFRP booms for a solar propelled sailcraft[J]. Acta Astronautica, 2006, 58(4): 185-196.
[3] Williams R B, Agnes G, Crumb D. Lightweight deployable sunshade concepts for passive cooling for space-based telescopes[C].The 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Schaumburg, USA, April 7-10, 2008.
[4] Appourchaux T, Auchère F, Antonucci E, et al. SOLARIS: solar sail investigation of the Sun//advances in solar sailing[M]. Berlin: Springer Berlin Heidelberg, 2014.
[5] Block J, Straubel M, Wiedemann M. Ultralight deployable booms for solar sails and other large gossamer structures in space[J]. Acta Astronautica, 2011, 68(7-8): 984-992.
[6] 李瑞雄,陈务军,付功义. 透镜式薄壁CFRP管空间伸展臂轴压屈曲分析及试验[J]. 宇航学报, 2012,33(8): 1164-1170. [Li Rui-xiong, Chen Wu-jun, Fu Gong-yi. Buckling analysis and experiment of lenticular CFRP thin-walled tube space boom under axial compression [J]. Journal of Astronautics, 2012,33(8): 1164-1170.]
[7] 蔡祈耀,陈务军,张大旭,等. 空间薄壁 CFRP 豆荚杆悬臂屈曲分析及试验[J]. 上海交通大学学报, 2016, 50(1): 145-151. [Cai Qi-yao, Chen Wu-jun, Zhang Da-xu, et al. Buckling analysis and experiment of cantilever thin-walled lenticular CFRP space boom [J]. Journal of Shanghai Jiaotong University, 2016, 50(1): 145-151.]
[8] Hu Y, Chen W, Li R, et al. Mechanical characteristics of deployable composite thin-walled lenticular tubes[J]. Composite Structures, 2016, 153: 601-613.
[9] Irwin R, Vander Veen J, Buchner-Santos E, et al. Low-mass deployable spacecraft booms[C]. American Institute of Aeronautics and Astronautics Space Conference & Exposition, Anaheim, USA, August 30-September 2, 2010.
[10] 丁峻宏,咸奎成,韩轩,等. 空间豆荚杆机构收展过程的并行仿真计算[J]. 宇航学报, 2011,32(3): 676-682. [Ding Jun-hong, Xian Kui-cheng, Han Xuan, et al. Parallel computing for simulation of stowing and development progress of space lenticular boom mechanism [J]. Journal of Astronautics, 2011,32(3): 676-682.]
[11] 李瑞雄,陈务军,付功义. 缠绕肋缠绕过程试验及力学行为分析[J]. 工程力学, 2012(11): 332-338. [Li Rui-xiong, Chen Wu-jun, Fu Gong-yi. Experimental and mechanical behavior of wrapping progress of lenticular wrapped-rib [J]. Engineering Mechanics, 2012(11): 332-338.]
[12] 蔡祈耀,陈务军,张大旭,等. 透镜式薄壁管状空间伸展臂压扁拉扁数值模拟与试验[J]. 上海交通大学学报, 2016(4): 601-607. [Cai Qi-yao, Chen Wu-jun, Zhang Da-xu, et al. Numerical simulation and flattening tests of compression and pulling of lenticular thin-walled tubular space booms [J]. Journal of Shanghai Jiaotong University, 2016(4): 601-607.]
[13] Chu Z, Lei Y. Design theory and dynamic analysis of a deployable boom[J]. Mechanism and Machine Theory, 2014, 71: 126-141.
[14] Hakkak F, Khoddam S. On calculation of preliminary design parameters for lenticular booms[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2007, 221(3): 377-384.
[15] Bai J B, Xiong J J, Gao J P, et al. Analytical solutions for predicting in-plane strain and interlaminar shear stress of ultra-thin-walled lenticular collapsible composite tube in fold deformation[J]. Composite Structures, 2013, 97: 64-75.
[16] Barbero E J. Introduction to composite materials design[M]. Tallahassee: CRC press, 2010.
通信地址:上海市东川路800号(上海交通大学)木兰船建大楼A302(200240)
E-mail: gjfmail@qq.com
陈务军(1969-),男,博士,教授。主要从事新型空间结构研究。本文通信作者。
通信地址:上海市东川路800号(上海交通大学)木兰船建大楼A302(200240)
E-mail: cwj@sjtu.edu.cn
(编辑:牛苗苗)
Analysis of the Flattening Force of Thin-Walled Lenticular CFRP Booms
GAO Ji-feng1, HU Jian-hui1, CHEN Wu-jun1, LU Shao-ming2, FANG Guang-qiang3, PENG Fu-jun3
(1.Space Structures Research Centre, Shanghai Jiao Tong University, Shanghai 200240, China;2.School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;3.Shanghai Institute of Aerospace System Engineering, Shanghai 201108, China)
The flattening force is studied for the design of the thin-walled lenticular carbon fiber reinforced polymer (CFRP) booms cross-section.Two thin-walled lenticular CFRP booms with different cross sections, lengths,layers and material parameters are selected. Their flattening force and deformation characteristics are analyzed by the experiments and numerical simulations. One approximation algorithm for the flattening force is established by assuming the nonexistence of the local contact deformation, and the cross-section is linearly deformed with equal curvature; the other is established by assuming the function of the partial contact deformation.Through analyzing the results of the experiments, numerical simulations and approximation algorithms, it is found that the flattening force and the cross-section show strong non-linear characteristics during the flattening process, and the approximation algorithm 2 can be used to estimate the flattening force.
Thin-walled lenticular boom; CFRP composite; Experimental analysis; Numerical simulation;Approximate algorithm; Flattening force
2016-11-29;
2017-03-08
国家自然科学基金(11172180);航天先进技术联合研究中心技术创新项目(USCAST2015-24)
V214.4
A
1000-1328(2017)05-0467-07
10.3873/j.issn.1000-1328.2017.05.004
高冀峰(1984-),男,博士生,主要从事复合材料及其在空间可展结构中的应用与研究。
