基于飞轮转速及其波动的气缸IMEP估计模型
2013-07-25甄龙信韦小刚滕晓雷
甄龙信 韦小刚 滕晓雷
燕山大学,秦皇岛,066004
0 引言
燃料燃烧产生的气力扭矩包含发动机和变速器控制的重要信息,平均指示压力(indicated mean effective pressure,IMEP)是衡量发动机单位容积对外做功的标准,是发动机扭矩管理系统中的重要参数[1],利用IMEP估计发动机的气力扭矩是一种行之有效的方法,因此准确估计IMEP是计算气力扭矩的基础。文献[2]研究了利用气缸压力传感器测量的气缸压力计算IMEP的快速实现方法。
发动机瞬时转速波动是由气缸压力、往复惯性力、摩擦力和负载等因素共同作用在曲轴切向的总扭矩波动的结果[3]。文献[4-5]利用飞轮转速信号根据发动机动力学模型估计出了瞬时指示压力,但该方法受发动机动力学模型精度的影响,还需要准确的负载估计模型。文献[6]将发动机指示扭矩分为循环平均扭矩和波动扭矩,利用MAP图法根据喷油量、点火提前角等标定平均扭矩,用飞轮角加速度变动求得波动扭矩,两者相加并变换后可得到各缸的IMEP。文献[7]通过实验数据分析表明单缸四冲程发动机的平均指示压力与飞轮转速波动和平均转速的乘积存在线性关系,且线性比例系数基本上不随空燃比、喷油量、润滑油温度等变化。
在以上IMEP的计算方法中,由于气缸压力传感器成本较高,一般只在第一缸安装,利用测量气缸压力计算IMEP的方法尚没有得到广泛应用。文献[4-6]提出的方法计算量大,不便于在线应用,文献[7]提出的方法计算量小,便于在线实现,但它是针对单缸发动机得出的结论。
本文根据文献[7]的思想,在分析四缸汽油机各缸IMEP与转速波动及平均转速之间关系的基础上,建立利用转速波动和平均转速估计气缸IMIEP的单工况模型以及稳态工况下的通用模型,在满足计算精度的前提下,有效减小计算量并降低成本,便于在线实现。
1 转速参数与IMEP相关性分析
表1所示为试验发动机的主要结构参数,表2所示为试验的6种不同工况。由表2可知热启动工况转速变动较大,属于非稳态工况,其余几个工况转速基本稳定,可以近似看作稳态工况。
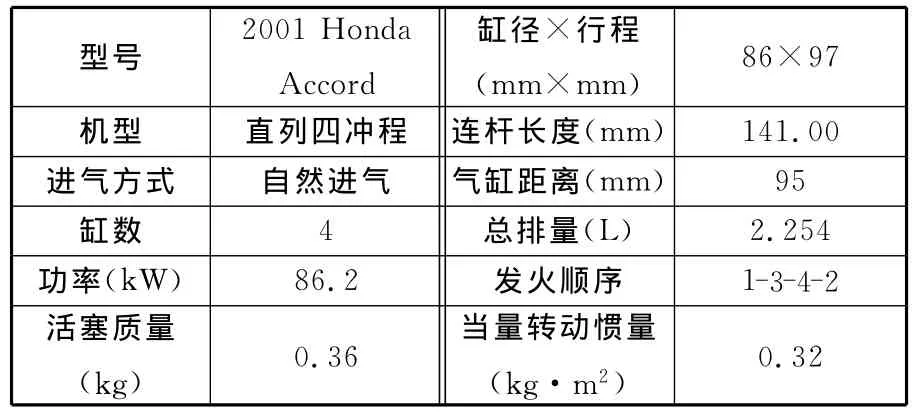
表1 发动机主要参数
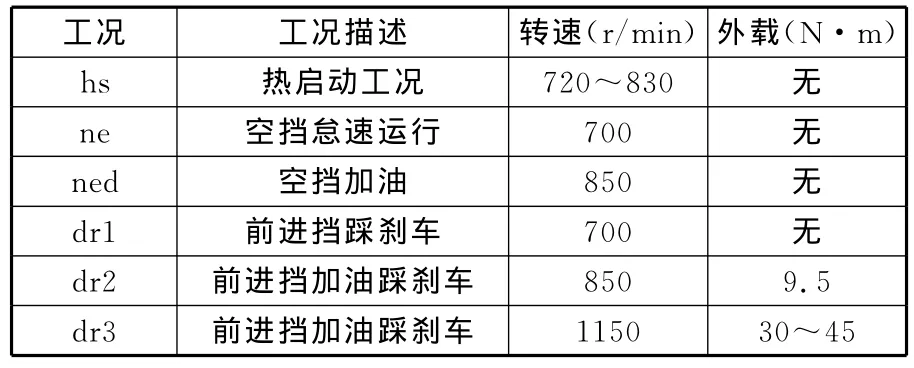
表2 所采集数据的运行工况
为了说明点火缸做功与转速波动的关系,定义瞬时平均指示压力为
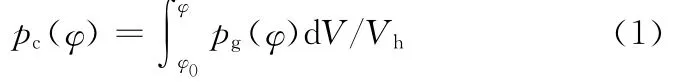
式中,pc为瞬时平均指示压力;φ为曲轴转角;φ0为初始角度;pg(φ)为气缸瞬时压力;V为气体瞬时体积;Vh为气缸有效工作容积。
图1所示为四缸机飞轮瞬时转速和某点火缸pc在一个工作循环内随曲轴转角的变化曲线,由图可知,点火缸做功区间与飞轮从最小转速nmin上升到最大转速nmax的区间基本重合,把对应的最小角速度和最大角速度分别记作ωmin和ωmax。令=(ωmax+ωmin)/2;Δω=ωmax-ωmin,为点火缸做功区间飞轮的平均角速度,Δω为点火缸做功区间飞轮的平均角速度波动。
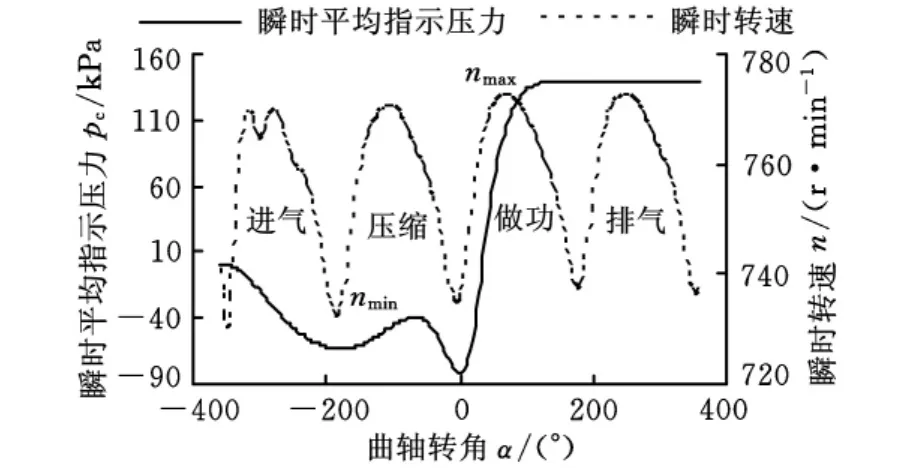
图1 燃烧缸瞬时平均指示压力与飞轮瞬时转速
按照文献[7]的方法,对四缸机各工况下的Δω和IMEP进行相关性分析:在每个工况下,计算每次发火过程的Δω和IMEP,分别将所有发火过程的Δω和IMEP组成两个变量Xω和XI,Xω和XI之间的线性相关系数为
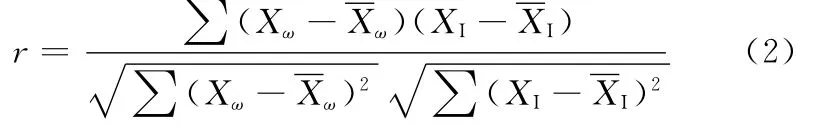
式中,为Xω的平均值;为XI的平均值。
利用式(2)计算各工况下Δω和IMEP之间的线性相关系数,结果如表3所示。由于四缸发动机各缸之间的相互影响,表3中每个工况的IMEP和Δω之间的线性相关系数都小于0.85,不具有文献[7]所描述的强线性相关性,故不能利用Δω直接计算IMEP。因此下文建立四缸汽油机IMEP与及Δω的关系模型。
表3 不同工况下Δω与IMEP的相关系数
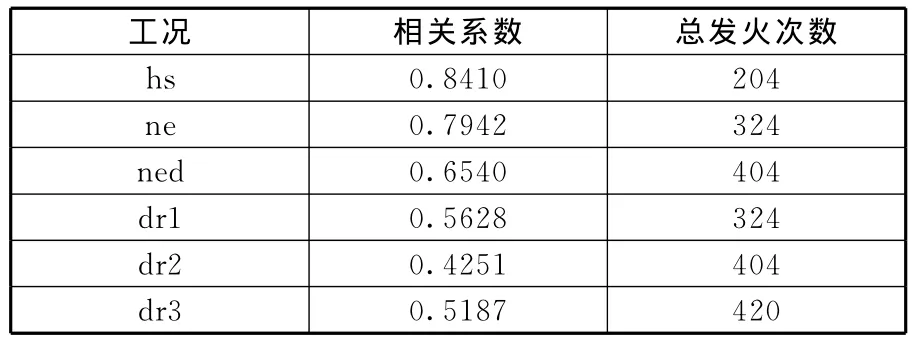
表3 不同工况下Δω与IMEP的相关系数
工况 相关系数 总发火次数hs 0.8410 204 ne 0.7942 324 ned 0.6540 404 dr1 0.5628 324 dr2 0.4251 404 dr3 0.5187 420
2 IMEP与转速参数关系建模
2.1 单工况模型
根据试验以及发动机做功理论可知:在一定负载下,发动机做功越多,飞轮平均转速越高;在一定转速下,点火缸做功越多,飞轮角速度波动量越大。根据上述发动机做功量与飞轮平均转速及转速波动之间的定性关系,提出利用飞轮平均角速度和角速度波动估计气缸IMEP的二元线性单工况模型:
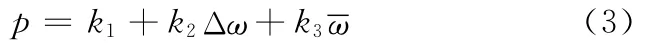
式中,ki为模型系数,i=1,2,3。
本文采用最小二乘参数识别法,以每次发火过程中飞轮平均角速度、角速度波动及IMEP的试验数据识别式(3)中模型系数。表4列出了ki在不同工况下的数值、IMEP估计值与实测值之间的相关系数以及相对误差。图2所示为各工况下IMEP估计值和实测值曲线。如图2所示,在每个工况下,IMEP的估计值和实测值随发火次数的变化趋势一致,两曲线基本重合。从表4可知,IMEP的估计值与实测值之间的相关系数都在0.9以上,为高度线性相关,ned工况的最大相对误差为7.95%,平均相对误差仅为2.21%,其他工况的误差都小于ned工况的误差,可见利用式(3)可对各工况IMEP进行精确的估计。
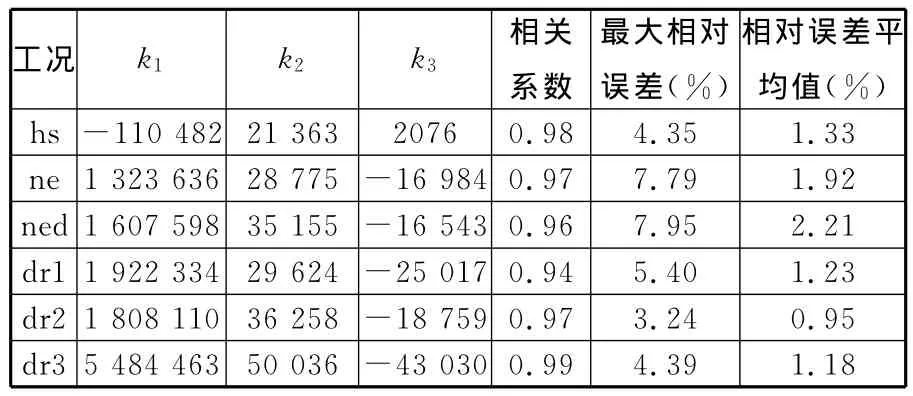
表4 不同工况下ki估计值和误差参数
如表4所示,式(3)的三个模型系数ki在每个工况都不一样,且hs工况下k1、k3的正负号与其他几个工况不同。利用此模型在线估计IMEP可以采用以下两个途径:
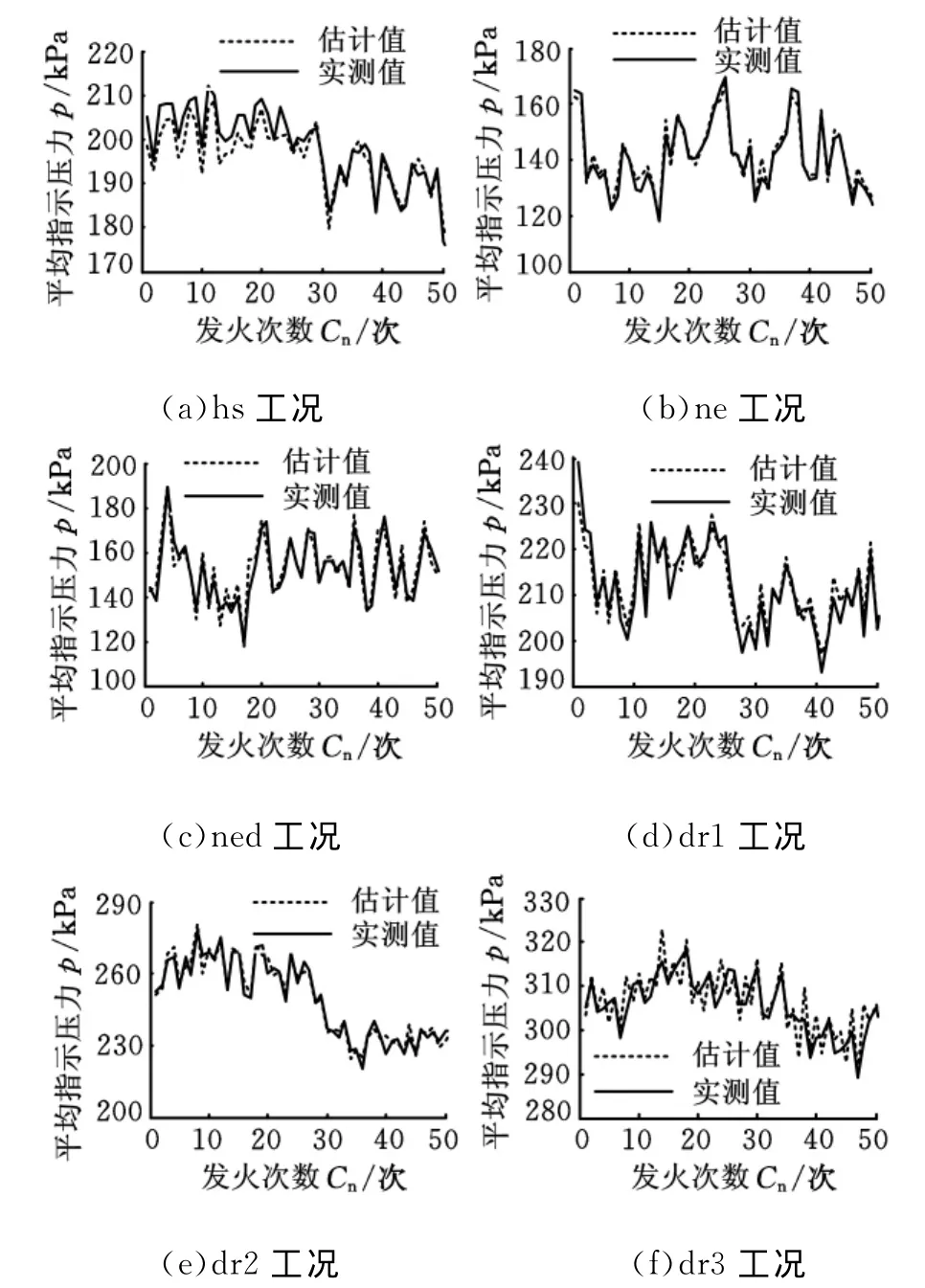
图2 各工况IMEP估计值和实测值
(1)通过测功机标定不同负载、转速下相应的ki值,根据负载、转速等条件在线判断发动机的工况,选择合适的ki值。
(2)利用每次燃烧过程中的其他已知变量估计ki,得到估计IMEP通用模型,通用模型的系数不随工况发生变化,无需判断发动机的工况。
2.2 稳态工况的IMEP估计通用模型
本文对建立估计IMEP的通用模型进行了尝试,但加入热启动这个不稳定工况后,估计误差明显增大。因此剔除热启动工况,建立了其他几个稳态工况的通用模型。
由单工况模型可知,每个工况的模型系数都不一样,这说明单工况模型的系数受转速、转速波动和负载的影响,因此尝试使用每次发火过程中的平均角速度、角速度波动Δω和平均负载TL的多项式模型代替式(3)中的ki(i=1,2,3)。模型的选用思路是采用不同次数和项数的多项式模型对估计的IMEP进行比较,选用精度最高的模型。基于上述原因和思路,ki选用表5所示的几种多项式模型,模型中的kij为k i模型的模型系数。表5同时列出了选用这几种模型时IMEP的估计误差平方和。

表5 ki的不同模型和对应IMEP估计误差平方和
本文利用文献[8]提出的简化刚性曲轴四缸汽油机动力学模型计算平均负载,即
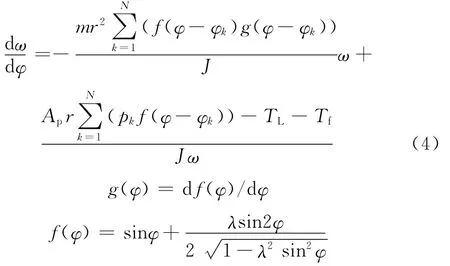
式中,ω为曲轴瞬时角速度;φk为第k缸相对于第一缸的发火相位,对于四冲程发动机,φk= (k-1)π;p k为第k缸压力;Ap为活塞面积;r为曲柄半径;Tf为摩擦扭矩;TL为负载;m为当量往复质量;J为当量转动惯量;λ为连杆比;N为气缸数量。
对于直列四缸发动机,当发火缸活塞运行到上止点时,气力扭矩和惯性扭矩为零,根据式(4)得
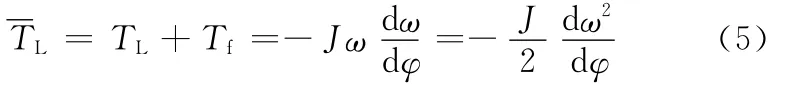
将表5中的ki模型逐一代入式(3),利用IMEP的实测值对系数kij进行识别。经过比较,当ki选用表5中的第7个模型时,IMEP的误差最小,将其代入式(3)得到的模型有多达18个参数。为了简化模型,去掉对估计误差影响较小的参数,最终得到的IMEP模型如下:

式(6)中包含13个参数,它对所有稳态工况的IMEP估计误差平方和为3.58×1010,式(5)中的参数估计值如表6所示。
IMEP估计值和实测值如图3所示,图4为图3的局部细节图,图5为IMEP相对误差图。从图3~图5可知,IMEP估计值和实测值非常接近,最大误差在8%以内。虽然未得到所有工况下IMEP的通用模型,但得到稳态工况下估计IMEP的通用模型可以显著减少工况的判断次数。
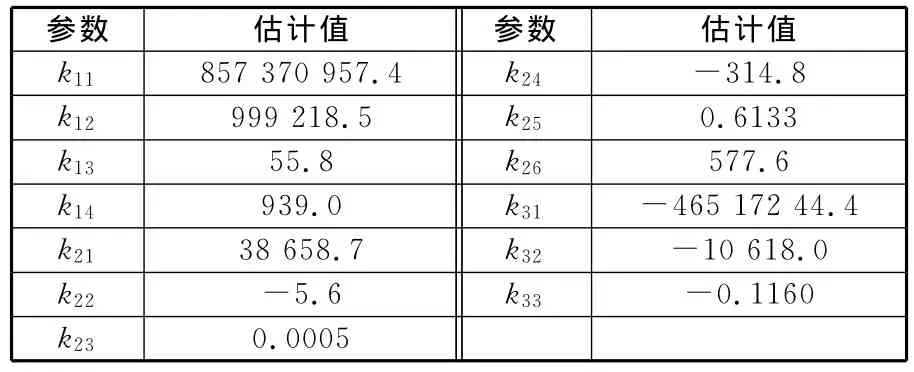
表6 kij的参数估计值
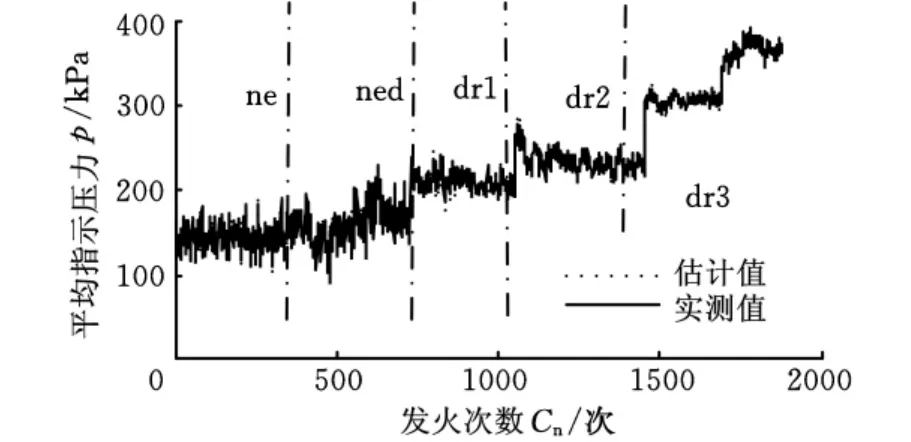
图3 IMEP估计值和实测值

图4 IMEP估计值和实测值局部细节图
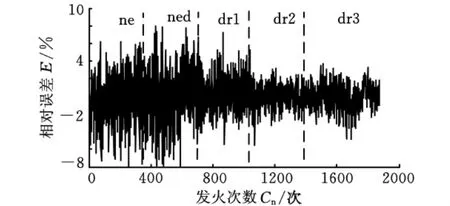
图5 IMEP估计相对误差
四缸机中曲轴每转两周(720°),各缸依次顺序完成点火,每缸的做功区间大致为180°,因此平均指示扭矩TI可以用平均指示压力表示:

图6所示为分别使用实测气缸压力计算的平均指示扭矩与基于飞轮转速估计的IMEP计算的平均指示扭矩之间的绝对误差,由图6可知绝对误差在3N·m以内,说明在低速工况下估计的IMEP可以分辨各缸做功差异。

图6 平均指示扭矩绝对误差
3 结论
(1)四缸发动机各缸平均指示压力与转速波动和平均转速的乘积不存在线性关系;各工况下各缸平均指示压力可以由每次燃烧区间对应的飞轮平均转速与转速波动组成的二元线性模型表示,从而得到估计平均指示压力的单工况模型。单工况平均指示压力模型的模型系数随着工况的不同而发生变化。
(2)将单工况模型的三个系数分别用关于转速波动、平均转速和平均负载的多项式模型代替,建立了稳态工况下估计平均指示压力的通用模型。通用模型估计的平均指示压力的相对误差在8%之内,平均指示扭矩的绝对误差在3N·m以内。
[1]Oh S,Kim D,Oh B,et al.Real-time IMEP Estimation and Control Using an In-cylinder Pressure Sensor for a Common-rail Direct Injection Diesel Engine[J].J.Eng.Gas Turbines Power,2011,133(6):1-9.
[2]万国强,黄英,张付军,等.面向控制的柴油机IMEP在线计算方法及试验[J].内燃机学报,2011,29(3):277-281.
Wan Guoqiang,Huang Ying,Zhang Fujun,et al.On-line IMEP Calculation Method for Diesel Engine Control and Experimental[J].Transactions of CSICE,2011,29(3):277-281.
[3]李建秋,欧阳明高,周明,等.发动机飞轮转速的传递函数分析[J].内燃机学报,2001,19(6):582-587.
Li Jianqiu,Ouyang Minggao,Zhou Ming,et al.Transfer Function Analysis of the Engines Flywheel Speed[J].Transactions of CSICE,2001,19(6):582-587.
[4]王赟松,褚福磊,郭丹.基于二阶滑模技术的内燃机气缸压力的估计[J].内燃机学报,2004,22(6):556-561.
Wang Yunsong,Chu Fulei,Guo Dan.Cylinder Pressure Estimation for Engines Using Second-Order Sliding Modes[J].Transactions of CSICE,2004,22(6):556-561.
[5]Williams J,Witter M C.Individual Cylinder IMEP Estimation Using Crankshaft Angular Velocity Measurements[J].SAE Paper,2001-01-0990.
[6]Rackmil C I,Mckay D,Malaczynski G W.Method for Estimation of Indicated Mean Effective Pressure for Individual Cylinders from Crankshaft Acceleration:US,7623955[P].2009-11-24.
[7]Kenji N,Tetsuya K,Yoichi T,et al.Estimation of Indicated Mean Effective Pressure Using Crankshaft Angular Velocity Variation[J].SAE Paper,2011-32-0510.
[8]刘世元,杜润生,杨叔子.利用转速波动信号在线识别内燃机气缸压力的研[J].内燃机工程,2000(3):37-43.
Liu Shiyuan,Du Runsheng,Yang Shuzi.Research on On-line Identification of In-cylinder Pressure by Using Speed Fluctuation Signal[J].Chinese Internal Combustion Engine Engineering,2000(3):37-43.
