电动车用交流异步电机宽速域控制策略

胡建军 旦高亮 秦大同

重庆大学机械传动国家重点实验室，重庆，400044

0 引言

电机驱动控制系统作为电动车辆的核心部件，其控制性能直接影响电动汽车的优劣。交流异步电机凭借其调速范围宽、效率高、可靠性好、性价比高的特点在电动汽车上得到广泛应用。

在交流异步电机的控制中，基于转子磁场定向的矢量控制方法控制理论成熟、方法简便，且可提高系统的动态性能［1－2］，但是传感器的安装使得系统成本增加，可靠性降低，因此基于无速度传感器的控制方法的研究逐渐兴起。其中，模型参考自 适 应 法 （model reference adaptive system，MRAS）因其控制模型简单、容易实现而应用较为广泛［3－4］。在MRAS中磁链和转速的估计非常重要，目前常用磁链模型有电流模型和电压模型两种［5］，电压模型中反电动势积分引起的计算误差会影响磁链计算的准确性，进而影响转速的辨识。

文献［6］提出了一种低通滤波器型磁通观测器来克服积分引起的误差，并采用一个饱和积分器对低通滤波器带来的误差进行补偿，但未对弱磁调速进行研究。由于电动汽车高速行驶的要求需要对电机进行弱磁控制，而传统的弱磁控制方法未考虑电压限制，从而造成磁链给定值计算不准确。文献［7］通过分析电机模型提出了一种基于电压限制的弱磁控制方法，但未改进磁链计算方法，并且没有对无速度传感器控制进行研究。

针对传统磁链计算中积分引起误差问题和弱磁磁链给定值不准确的问题，本文在分析电机矢量控制数学模型的基础上，设计了恒转矩区和弱磁区的磁链控制器和MRAS转速辨识系统，提出了一种宽速域的电机转速控制策略并进行仿真与实验分析。

1 异步电机的数学模型

电机模型是一个高阶、非线性、多变量、复杂的数学模型。为了便于控制，经过三相静止坐标系/两相静止坐标系变换（简称3/2变换）、两相静止坐标系（设定为α－β轴系）/两相同步旋转坐标系（设定为M－T轴系）变换（简称2s/2r变换）得到同步旋转坐标系下的异步电机矢量控制系统模型：

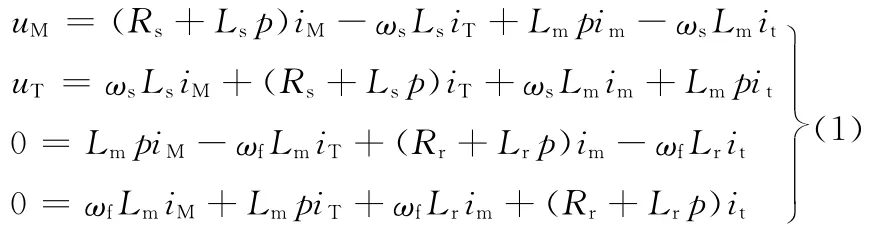
式中，uM、uT、iM、iT分别为定子绕组 M轴和T轴的电压、电流分量；im、it分别为转子绕组M轴和T轴的电流分量；Rs、Rr分别为定子、转子绕组的电阻；Ls、Lr分别为定子、转子绕组电感；Lm为定转子间的互感；ωs为定子同步电角速度；ωr为转子的电角速度；ωf为转差且ωf＝ωs－ωr；p表示d/dt，称为微分算子。

在转子磁场定向下，可以得到基于矢量控制原理的系统控制表达式：

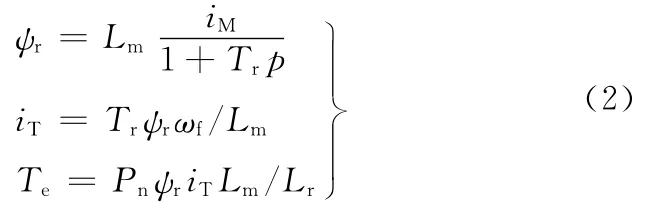
式中，Te为电磁转矩；ψr为转子磁链；Tr为转子时间常数，Tr＝Lr/Rr；Pn为磁极对数。

式（2）在转子磁场定向下将交流电机等效为直流电机，实现了驱动系统的降阶解耦控制。

图1 异步电机控制系统简图

在矢量控制理论的基础上建立闭环反馈控制系统模型，该模型结构如图1所示，系统由电机模块、逆变器模块、磁链观测器、坐标变换模块、转速外环、电流内环和信号采集模块组成。将MRAS模块计算得到的电机转速n与上层控制单元发给电机驱动控制系统的转速命令n＊作比较，将其偏差输入转速调节器，产生电机的转矩命令，经过计算获得实现该转矩所需的电流给定值。同时磁链控制器输出磁通给定值，产生励磁电流。信号采集装置检测到的电机定子三相电流经过坐标变换得到M－T坐标系下的两个电流分量iM、iT。将与iM、与iT的偏差分别作为两个电流PI调节器的输入，最终产生电压分量实现了电压的解耦。将经2s/2r逆变换输入到空间矢量脉宽调制SVPWM模块中，从而产生逆变器的脉冲控制量，使电机能够以给定的转速运转。

2 基于MRAS的电机控制策略

磁链在异步电机的控制中是十分重要的变量，其计算是否准确直接决定系统控制性能的好坏。

2.1 磁链观测器设计

定义L′s＝σLs＝Ls－/Lr，σ称为漏磁系数，式（1）经坐标变换得到α－β轴系转子磁链的表达式：

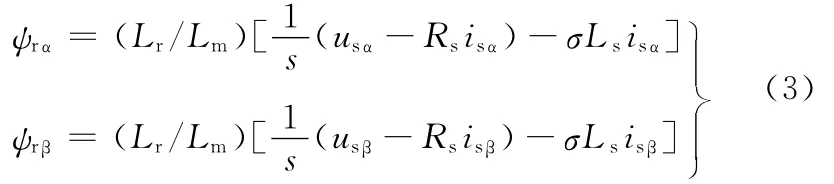
式中，usα、usβ、isα、isβ分别为定子在 α、β轴上的电压、电流分量；ψrα、ψrβ分别为转子磁链在α、β轴上的分量；s为拉普拉斯算子。

式（3）中电流、电压信号的采集过程会带来偏置误差，直接进行积分计算会造成较大的磁链计算误差，从而影响系统的控制效果。通常情况下采用低通滤波器［8］（low－pass filter，LPF）代替积分器来克服该误差，即用1/（s＋ωa）代替1/s，其中ωa代表滤波器的截止角频率。

当usα、isα分别加入直流偏置后，经过计算可知，采用LPF可减小积分环节的偏置误差，使磁通的计算结果接近真实值；进一步分析可知，采用LPF会导致幅值的衰减和相位的变化（表1），因此需要对LPF的计算结果进行补偿。

表1 采用LPF的输出响应

截止角频率的选取也非常重要，合适的角频率可以获得较好的直流抑制能力，确保系统运行的稳定性。截止角频率一般为同步角频率的20%～30%时［9］，可以得到较佳的磁链观测效果。

采用截止角频率可调的饱和积分器来补偿LPF的误差，则磁链的表达式为

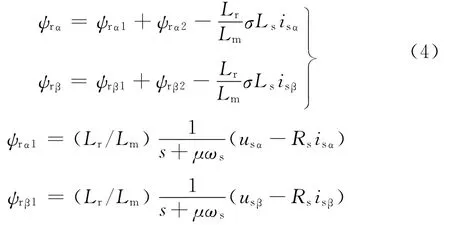
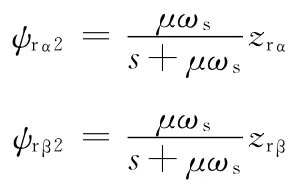
式中，μ为系数；zrα、zrβ为饱和积分器的输出量。

该误差补偿的工作原理为：采用直角－极坐标互换的方法实现限幅。对ψrα、ψrβ的计算结果进行直角－极坐标变换得到磁链幅值ψr和相应的相位角。当磁链幅值小于最大限幅值时，磁链幅值不受限，即zrα＝ψrα1＋ψrα2，zrβ＝ψrβ1＋ψrβ2；反之，磁链幅值的输出为最大限幅值，即zrα、zrβ分别为限幅值经极坐标－直角坐标变换所产生的两个分量；而限幅环节中相位不变。在磁通小于限幅值时，该环节与积分器等效但抑制了直接积分的误差。在磁通大于限幅值时以限幅值产生的分量来计算补偿分量，最终得到的磁链失真很小。

2.2 转速估计

为了确保在没有转速传感器的情况下也能实现转速控制，常常采用MRAS建立转速估计系统。根据计算得到的磁链信息建立转速自适应规则，使得转速辨识值与真实值吻合，实现驱动系统的无速度传感器控制。

基于两相静止坐标下的电机模型，根据转子磁链、定子电压、电流分量构建MRAS系统，以改进电压模型（式（4））为参考模型，以电流模型为可调模型。其中电流模型的表达式为

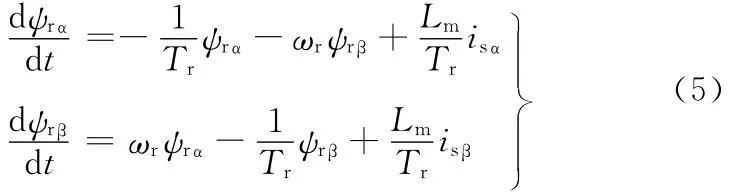
根据Popov超稳定性理论，可以得到转速的自适应规律：

式中，kp、ki分别为比例系数和积分系数；带＾上标的变量表示估计量。

2.3 弱磁区磁通给定值的计算

电机在额定转速以上运行时，受实际电压的限制，仅可通过降低磁链来提高转子转速。传统的磁链转速反比法不涉及磁链和转矩间电压电流的合理分配，磁链计算的准确性差。因此，本文在分析电机的弱磁运行性能的基础上提出了一种考虑电压限制的磁链计算方法，能获得准确的磁链给定值，从而实现对弱磁区的转速控制。

电机在弱磁区工作时，定子电阻压降很小，可以忽略不计。根据M－T轴系下的电机方程式可得稳定状态时的定子电压方程：

电机弱磁特性受其设计参数和逆变器的最大输出电压usm的限制［10-11］，其满足的条件为

其中，usm与直流电源的电压udc和采用的逆变器的输入控制信号的调制方法有关，本文采用SVPWM方式，取usm＝udc/，ism为电机工作时的最大电流，一般取为电机的额定电流。

稳态时的转子磁链ψr＝LmiM，转矩的表达式为

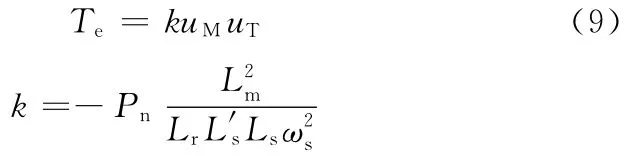
定义F＝Te/k，在同步转速一定的情况下，k为常数，F与Te成正比关系。因此可以用F来代表转矩。为充分利用母线电压，采用恒压弱磁控制，F的表达式为

当uM增大时，F的值随电压的变化先增大后减小。在dF/duM＝0时，其值达到最大，此时电压和同步转速ωC满足：

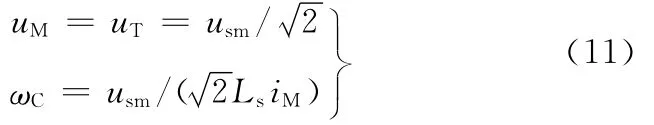
基于以上分析，所制定的电机磁链控制策略如下：①恒转矩区工作时，由于转速较小其所需要的电压不会超过规定的电压限制值，此时磁链为给定的常数；② 在弱磁区内运行时，当uM≤usm/时，随转速的升高，｜uM｜增大，转矩电流iT随之增大，输出转矩也增大，转矩电流和转矩的变化是相同的，在电压和电流限制圆相交处可以得到最大的转矩输出，磁链的控制量为

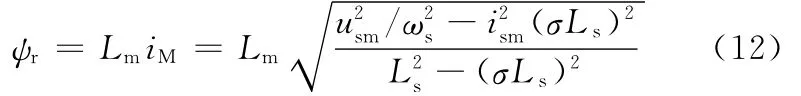
当uM＞usm/时，随转速的升高，转矩电流和输出转矩的变化趋势是相反的，为了保证输出转矩最大，磁链的控制量为

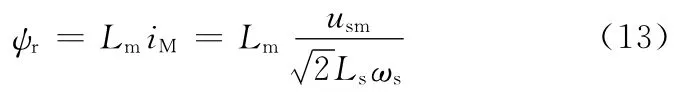
图2为所设计的磁链控制原理图。直接采用转速来判断恒转矩区和弱磁区，方法简单快速，避免了用定子电压判断带来的复杂计算和干扰，在弱磁区同时考虑母线电压、同步转速，相比传统的转速反比法，磁链计算较为准确，确保电机在弱磁区输出的转矩最大。

3 仿真与实验分析

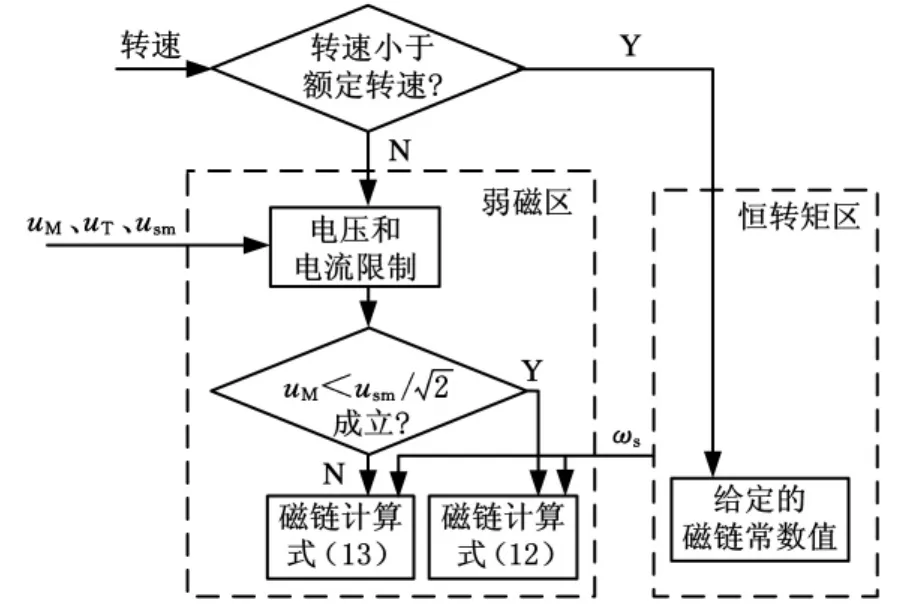
图2 磁链控制流程图

为验证所制定的电动车用交流异步电机宽速域控制策略的合理性和有效性，基于MATLAB/Simulink仿真平台，建立了基于MRAS的电机控制系统模型。仿真参数如下：三相交流异步电机额定转矩为300N·m，额定转速为1300r/min，磁极对数为2，阻尼系数B＝0.1，定子电阻Rs＝0.087Ω，定子绕组电感Ls＝0.0355H，转子电阻Rr＝0.228Ω，转子绕组电感Lr＝0.0355 H，定转子间的互感Lm＝0.0347H，转子磁链值为0.84Wb，所采用的直流电源的电压为420V。

仿真中，首先设定起始目标转速为400 r/min，0.6s时目标转速阶跃到800r/min并保持不变，1s时又降到600r/min并保持不变。电机开始时为空载运转，在1.8s时载荷变为50N·m并保持不变。图3所示为相应的转矩、转速的响应曲线，开始时系统以400r/min的目标转速进行控制，图3b中实际转速很快从0升至目标转速，响应较为迅速。此时转矩的变化如图3a所示，在起始阶段由于实际转速与目标转速相差很大，输出的转矩也较大；而随着转速跟踪到目标值时，转矩也很快减小到0并保持稳定。之后的加减速过程响应与之相同。从图3中可以看出控制系统在电机加减速过程中能够实现对目标转速的快速响应，动态控制效果较好。

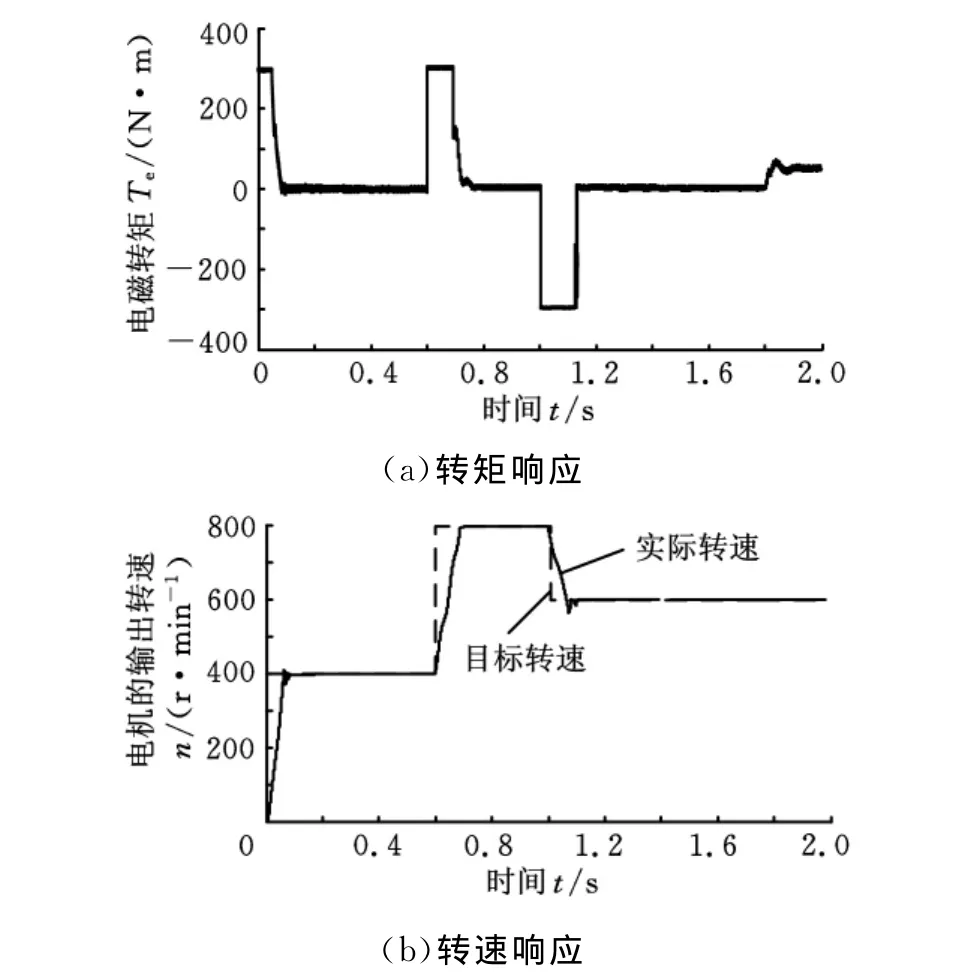
图3 恒转矩区的转矩、转速响应曲线

为了检验电机从恒转矩区进入弱磁区的转速控制效果，设定系统起始目标转速为800r/min，0.6s加速至1400r/min并保持不变。图4为对应的实际转速的响应曲线，可以看出MRAS系统的实际转速能较好地跟踪目标转速，表明该系统在恒转矩区和弱磁区都能获得较好的控制效果。

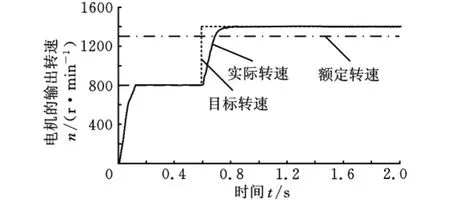
图4 从恒转矩区进入弱磁区的转速响应曲线

图5a为响应图3所示的目标转速时的转子磁链幅值的变化曲线图，图5b为响应图4中的目标转速时的转子磁链幅值的变化曲线图。从图中可以看出，恒转矩区调速时转子磁链为磁链给定值；而进入弱磁区后，实际磁链值小于给定值，验证了弱磁控制策略的合理性。

图5 恒转矩区和弱磁区控制时的磁链比较

为了验证所提控制策略的正确性，搭建了图6所示的交流异步电机（7.5k W）矢量控制实验平台，利用PM100DX电机控制器来实现电机的转速控制。结合Drivesoft软件进行控制系统建模，通过串口RS232把控制程序刷入控制器中，在无负载的条件下进行电机调速实验，其实验结果如图7所示。从图中可以看出，在恒转矩区和弱磁区应用该控制算法均能使电机实际转速较好地跟踪目标转速，超调小、响应快、动态响应性能好，从而验证了所提控制策略的正确性和合理性。

图6 控制系统的实验平台

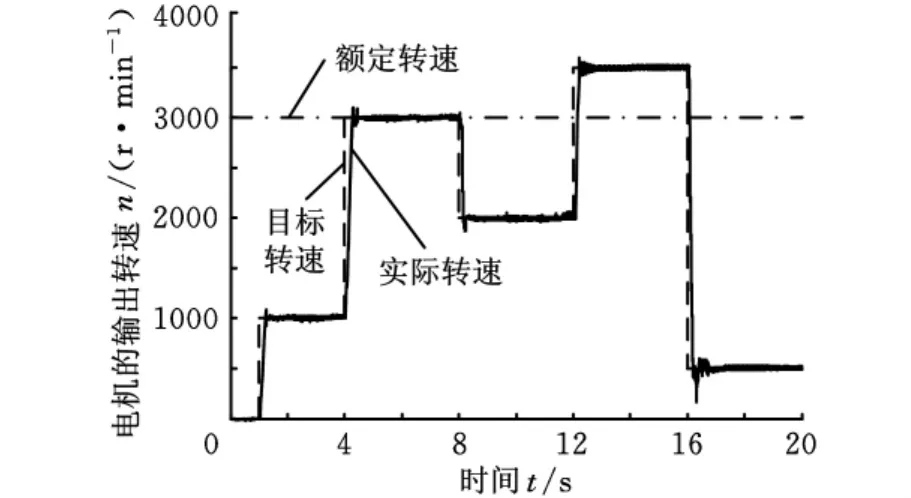
图7 转速控制时的响应曲线

4 结论

（1）利用矢量控制理论对交流异步电机动态模型进行了分析，建立了转子磁场定向下的基本控制方程式。

（2）在MRAS的转速估计中，采用一种基于低通滤波的饱和反馈积分器的方法改进原来的电压型磁链模型，使得磁链观测较为准确。分析了电机的弱磁运行性能，提出了基于输出最大转矩的磁链控制方法，使得弱磁区的磁链给定值的计算较为准确。制定了基于MRAS的宽转速范围内的电机驱动控制策略，仿真及实验结果表明，应用所提控制方法能够迅速的实现目标转速，动态响应较好，验证了该策略的可行性和有效性。

［1］Chen Zhongwei.Induction Motor Vector Control System Based on Anti－windup Controller［C］//Proceedings of the 6th IEEE Conference on Industrial Electronics and Applications.Beijing，2011：2729－2732.

［2］程飞，过学迅.电动汽车用电机及其控制技术研究［J］.防爆电机，2006，41（5）：14－19.

Cheng Fei，Guo Xuexun.Study on Motor for Electric Automobile and Its Controlling Technology［J］.Explosion Proof Electric Machine，2006，41（5）：14－19.

［3］Haron A R，Idris N R N.Simulation of MRAS－based Speed Sensorless Estimation of Induction Motor Drives Using Matlab/Simulink［C］//First International Power and Energy Conference.Putrajaya，2006：411－415.

［4］Gadoue S M，Damian G，Finch J W.Sensor－less Control of Induction Motor Drives at Very Low and Zero Speeds Using Neural Network Flux Observers［J］.IEEE Transactions on Industrial Electronics，2009，56（8）：3029－3039.

［5］王成元，夏家宽，孙宜标.现代电机控制技术［M］.北京：机械工业出版社，2009.

［6］王高林，陈伟，杨荣峰，等.无速度传感器感应电机改进转子磁链观测器［J］.电机与控制学报，2009，13（5）：638－642.

Wang Gaolin，Chen Wei，Yang Rongfeng，et al.Improved Rotor Estimator for Sensor－less Induction Motor［J］.Electric Machines and Control，2009，13（5）：638－642.

［7］张星，瞿文龙，陆海峰，等.一种异步电机定子磁链弱磁控制方法［J］.电工电能新技术，2008，27（3）：54－57.

Zhang Xing，Qu Wenlong，Lu Haifeng，et al.Stator Flux Weaken Method for The Induction Motor［J］.Advanced Technology of Electrical Engineering and Energy，2008，27（3）：54－57.

［8］Silveira A W F V，Andrade D A，Bissochi C A，et al.A Comparative Study between Tree Philosophies of Stator Flux Estimation for Induction Motor Drive［C］//Proceedings of IEEE International Electric Machines and Drives Conference.Antalya，2007：1171－1176.

［9］孙大南，林文立，刁利军，等.改进型感应电机电压模型磁链观测器设计［J］.北京交通大学学报，2011，35（2）：94－98.

Sun Danan，Lin Wenli，Diao Lijun，et al.Improved Voltage Model Flux Observer Design of Induction Machine［J］.Journal of Beijing Jiaotong University，2011，35（2）：94－98.

［10］Domenico C，Giovanni S，Angelo T，et al.A Robust Method for Field Weakening Operation of Induction Motor Drives with Maximum Torque Capability［C］//Conference Record of the 2006 IEEE Industry Applications Conference－IAS Annual Meeting.Tampa，2006：111－117.

［11］Michele M，Luca Z，Angelo T，et al.Domenico1 Stator Flux Vector Control of Induction Motor Drive in the Field Weakening Region［J］.IEEE Transactions on Power Electronics，2008，23（2）：941－949.