功的计算到底是用物体位移还是作用点位移

2013-01-11黄正玉

物理通报 2013年10期

黄正玉

(深圳市第二实验学校广东深圳 518021)

功是物理学中最基本的概念之一, 也是力学教学的重要课题, 但学生对机械运动范围内，功的定义和功的计算常有疑问.计算功的位移到底是指力的作用点的位移还是物体的位移呢？近读文献[1]一文，收益颇多.此文作者认为两者都可以,但笔者有不同看法，现试图就此问题进行探讨.

1 问题展示

【例1】质量为m的物体放在光滑的水平面上，绳经滑轮与水平方向成θ角，用大小为F的力拉物体，如图1所示.将物体由A点拉到B点，前进s.求拉力F对物体所做的功为多少.

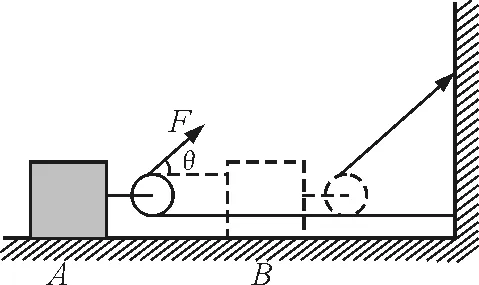
图1

解析：已知力F是作用在绳上的，而位移s是物体的位移，不是力F的作用点的位移.根据恒力功的公式W=Fscosθ中位移s应该是力的作用点的位移，所以,需要先求力的作用点的位移.

根据力的作用点定义功

W=Fs′cosβ

由图2几何关系得出AB=BC=s，则

θ=2βs′=2scosβ

所以

W=Fs′cosβ=F×2scos2β

又

θ=2β

得

W=Fs(1+cosθ)

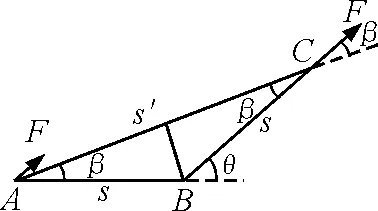
图2

【例2】如图3(a)所示，一个长为L，质量为M的长方形木块，静止在光滑水平面上，一个质量为m的物块(可视为质点)，以水平初速度v0从木块的左端滑向右端，设物块与木块间的动摩擦因数为μ，当物块与木块达到相对静止时，物块仍在长木块上，求木块的最小长度和系统机械能转化成内能的量Q.

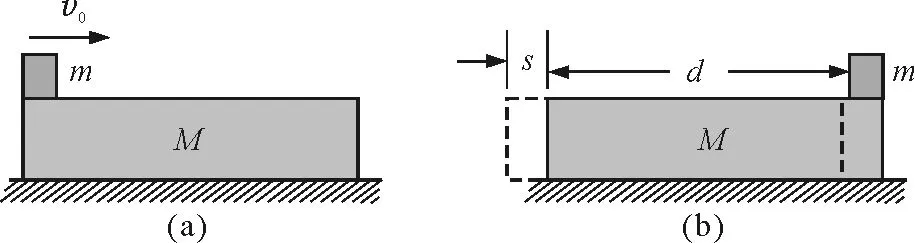
图3

解析：可先根据动量守恒定律求出物块m和木块M的共同速度，再根据动能定理或能量守恒求出转化为内能的量Q.

如图3(b)所示，对物块，滑动摩擦力Ff做负功，由动能定理得

对木块，滑动摩擦力Ff做正功，由动能定理得

又以物块、木块为系统，系统在水平方向不受外力，根据动量守恒定律，则

mv0=(m+M)vt

而系统减少的机械能为

Ff(d+s)-Ffs=Ffd

解得

系统机械能转化为内能的量为

2 问题分析

以上两个例题的解答都是正确的.但计算功的时候位移却有两种不同的理解.例1中，功等于力与力的作用点的位移的乘积.例2摩擦力做功是用摩擦力乘以物体的位移.

相反，如果例1中用物体的位移，则会得出W=Fscosθ的错误结论.同样,例2中的位移如果理解为作用点的位移，那么,两个摩擦力的作用点的位移是相同的，所以,两个摩擦力做功将互为相反数，将得出两摩擦力总功和为零，系统动能不变，当然也就得出发热量为零的错误结论.

功的定义W=Fscosθ中的位移s到底是物体位移还是作用点位移呢？

3 理论探微

动能定理是从牛顿第二定律推导得出，因而不管是位移s还是速度v，都必须是惯性参考系中的位移和速度.通常取地面为参考系，也就是相对地面的位移和速度.

对例1的求解有以下两种方法.

方法1：力F的受力物体是绳子端点，力F做的功既可以理解为F对细线端点做的功,也可理解为F通过绳子滑轮装置对物体做的功.但如果理解为力对绳子做的功，那么,实际上力的作用点的位移就是绳子端点的位移，本质上也就是受力物体的位移,同样s也是受力物体受力点的位移.

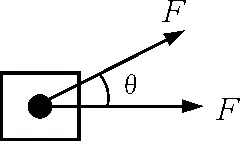
图4

方法2：根据能量守恒，例1中力F做的功最终等于物体动能的增量，因而也就等于物体合外力做的功.而物体相当于受夹角为θ，大小均为F的两个恒力作用(图4)，发生的位移为s，故做功

W=(F+Fcosθ)s=F(1+cosθ)s

公式中的位移仍然还是指物体的位移，当然s也是受力物体受力点的位移.

对例2，如果应用质点动能定理，也就是对单个物体应用动能定理，计算摩擦力对物块做功要用物块对地的位移，计算摩擦力对木块做功要用物块对地的位移.不能用摩擦力作用点的位移.不难看出,一对滑动摩擦力的作用点的位移大小是相等的，如果用作用点位移计算功，将得出一对滑动摩擦力做功大小相等的错误结论.

当然，若应用质点系的动能定理，或者说对系统应用动能定理，那么，系统的动能改变量将等于外力做功和内部非保守力做功的代数和.求得

等式左边-μmgd指摩擦力对系统做的总功，其绝对值等于系统发热量Q，或者说系统内能的增量.其中的d，实际上是两物体对地的位移之差，或者说两物体的相对位移，同样，也不能理解为力的作用点的位移.本题中两受力物体力的作用点相对地面的位移大小相等，但两受力物体受力点的位移是不等的.利用受力物体受力点的位移计算功，所得结论和动能定理结论一致.再次说明，计算功的公式中的位移s应该是受力物体受力点的位移.