对2016年江苏卷第14题的进一步探析和论证
2021-01-29安徽邢乐萍
◇ 安徽 邢乐萍
深刻理解题设物理条件,是解决物理综合问题的关键.在一道高考试题的研究中,学生对题设条件提出了质疑,本文对此做了进一步探析和论证,并指出:要使物块不脱离斜面,斜面倾角须满足一定的条件,不能取任意值;物块不脱离斜面时,绳子不会松弛.
1 高考真题回放和学生的质疑
例(2016年江苏卷第14题)如图1所示,倾角为α的斜面A被固定在水平面上,细线的一端固定于墙面,另一端跨过斜面顶端的小滑轮与物块B相连,B静止在斜面上.滑轮左侧的细线水平,右侧的细线与斜面平行.A、B的质量均为m.撤去固定A的装置后,A、B均做直线运动.不计一切摩擦,重力加速度为g.求:
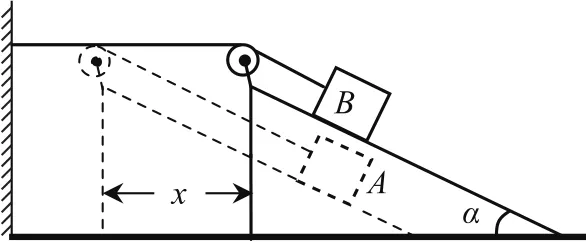
图1
(1)A固定不动时,A对B支持力的大小FN;
(2)A滑动的位移为x时,B的位移大小s;
(3)A滑动的位移为x时的速度大小vx.
高考参考答案(1)A固定不动时,对物块根据平衡条件,支持力的大小FN=mgcosα.
(2)根据几何关系sx=x(1-cosα),sy=xsinα,,由以上各式得
(3)物块B下降高度sy=xsinα,对A、B系统,由机械能守恒定律有,结合,则有
学生对第(2)、(3)两问的解析提出了质疑:
1)题设条件“A、B均做直线运动”,但题设中并没有说物块B始终在斜面上,为何上述解析默认了物块B始终在斜面上呢?也就是说斜面倾角α取任意值时,物块B均不会脱离斜面吗?2)若物块不脱离斜面,绳子会不会松弛呢?3)若物块B脱离了斜面,还能做直线运动吗?
2 对学生质疑的进一步探析和论证
其实学生的质疑,是对题设条件的逻辑关系的质疑.若物块不脱离斜面,则物块做直线运动(这个命题的正确性比较容易证明,详见下面的论证),即题设条件“A、B均做直线运动”是物块不脱离斜面的必要条件,但其充分性,也就是逆命题“若物块B做直线运动,则物块不脱离斜面”的正确性并非不证自明的,逻辑严密的学生解答此题时就卡在这里.因为他们知道“原命题正确,其逆命题不一定正确”,而在没有证明的前提下,他们不敢直接应用逆命题“若物块B做直线运动,则物块不脱离斜面”求解该题.可见,参考答案的解析缺乏逻辑严密性.
2.1 物块B做直线运动的论证
若物块B不脱离斜面,设物块相对于斜面的速度为v相对,由于绳子不可伸缩,则v相对=vA,根据速度合成(绝对速度=牵连速度+相对速度),物块的速度vB是斜面速度vA=vx和v相对的矢量和,如图2所示.因此,物块B的速度大小
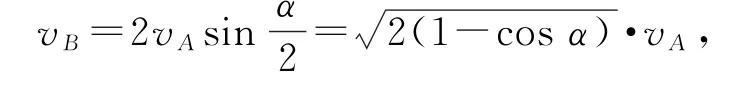

图2
这样,已证明了“若物块B不脱离斜面,则物块B做直线运动”是正确的,即物块B做直线运动是物块不脱离斜面的必要条件.但其逆命题“若物块B做直线运动,则物块不脱离斜面”不一定是正确的,即物块B做直线运动是不是物块不脱离斜面的充分条件,尚需进一步证明后才能应用.笔者认为在中学物理的范畴内这个充分条件无法证明,期待老师们做进一步研究证明.因此,笔者认为题目中应明确已知“物块B不脱离斜面且做直线运动”.
2.2 物块不脱离斜面的条件的进一步探析

图3
假设物块不脱离斜面,任意时刻由于斜面后退的速度大小等于物块相对于斜面运动的速度的大小,所以斜面加速度a与物块相对于斜面的加速度a相对大小相等,物块对地的加速度是斜面加速度a与物块相对于斜面的加速度a相对的矢量和,如图3所示.根据牛顿第二定律,在水平方向上对斜面和物块整体有F=ma+m(a-acosα),在平行于斜面方向对物块有

在垂直于斜面方向对物块有
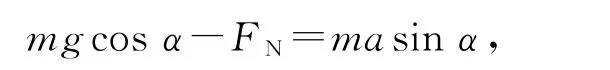
解得
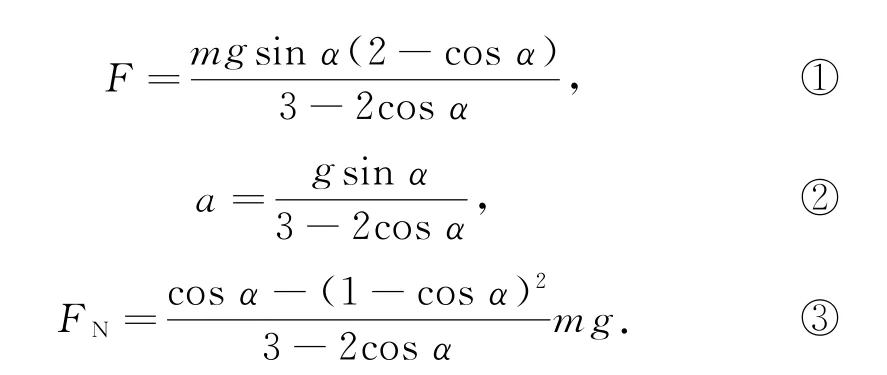
对式①~③讨论如下:
2)物块B不脱离斜面时,由图3中加速度矢量关系和式②可知,当物块不脱离斜面时,斜面和物块加速度恒定(大小和方向不变),物块和斜面做匀加速直线运动.
因此,题目第(2)问可由匀变速直线运动的公式得A滑动的位移为x时的速度大小
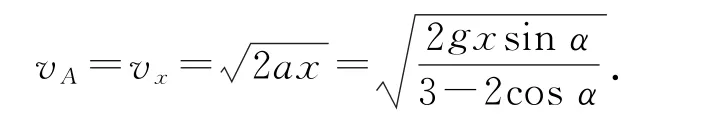
3)由式③可知,FN并不总是大于零.要使物块不脱离斜面,须有,则需满足cosα-(1-cosα)2>0,即物块不脱离斜面的条件是:斜面倾角需满足(取“=”时,物块在斜面上且FN=0,是脱离和不脱离的临界条件).
可见,要使物块不脱离斜面,斜面倾角不能取任意值,但题中并没有说明斜面倾角的范围,物块有可能脱离斜面,因此学生的质疑是有道理的.
综上所述,证明“若物块B做直线运动,则物块不脱离斜面”或者它的逆否命题“若物块脱离斜面,就不做直线运动”的正确性是解题的关键,但高中学生很难证明这个问题.思维严谨的考生想证明却证明不了,反而在此处形成解题的思维障碍,不能顺利解答.因此,笔者认为题设中应明确已知“物块B不脱离斜面且做直线运动”更好.
