飞轮控制的欠驱动刚体航天器姿态控制器设计

李公军

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

飞轮控制的欠驱动刚体航天器姿态控制器设计

李公军1，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

针对“三正交加料装”反作用轮系统中某两个本体轴上的飞轮失效的欠驱动情况，研究了航天器的姿态控制问题.在系统初始角动量为零的条件下，设计分段解藕控制律，实现了姿态稳定.采用欧拉角描述法建立了欠驱动航天器的姿态动力学方程和运动学方程.在系统初始角动量为零的条件下，通过分析方程的解藕特性，设计了分段解藕控制律.该方法经过6次机动控制，可实现姿态稳定.数值仿真验证了方法的有效性.

欠驱动;航天器;姿态稳定;解藕控制;反作用飞轮

所谓欠驱动航天器是指由于姿控系统某些执行机构故障，使得剩下的执行机构所提供的独立力矩维数小于3.一方面，空间环境的恶劣性和执行机构的机电一体化特性，使得执行机构常常发生故障，因此，研究欠驱动情况下航天器的姿态控制问题很有实际意义.另一方面，由于不满足Brockett[1]能稳条件，以研究定常光滑状态反馈为主的现代非线性控制方法不能直接用于解决欠驱动系统的稳定问题，必须寻找新的工具和方法，因此研究欠驱动航天器的姿态控制问题还具有很大的理论意义[2].

关于欠驱动航天器的研究，国内外已经有很多研究成果.Crouch[3]首先对航天器姿态的可控性进行了研究，他给出了当推力器所提供的独立力矩维数分别为1、2、3时，系统可控的充分必要条件.同时，文中还指出，对于采用角动量交换装置作为姿控系统执行机构的航天器，在系统的总角动量不为零的情况下，如果系统的输入维数小于3，则完整姿态不可控.Byrnes和Isidori等[4]的研究表明，由于不满足Brockett[1]必要条件，只有两个控制输入的刚体航天器，不能由连续定常的状态反馈控制律来渐近稳定航天器姿态，即只能采取时变或者不连续的控制律.

在上述研究成果的基础上，关于欠驱动航天器的研究可分为两类，一类考虑推力器作为执行机构[2，5-11]，另一类考虑角动量交换装置作为执行机构[12-19].其中，文献[12-16]考虑飞轮作为执行机构，文献[17-19]考虑CMG作为执行机构.文献[12]采用欧拉角描述航天器姿态，通过分析方程的解耦特性，设计了分段解耦控制律.该方法经过6次机动，可实现姿态稳定.该控制律有两个优点:一是有限时间内实现稳定，而非渐近稳定;二是通过选择控制器参数，可以将力矩控制在合理的范围内.文献[15]在姿态偏差为小量的情况下，利用Backstepping法设计控制律，实现了本体系相对轨道系的三轴稳定.但是，当非欠驱动轴姿态角很小，而欠驱动轴姿态角较大时，该方法可能会出现力矩较大的情况.文献[9]对此进行了研究，所设计的控制律可大幅降低控制量.但是，该控制律只是保证了有界性，并没有给出界的表达式.

从已有文献[12，14-15]来看，针对飞轮作为姿控系统执行机构的情况，研究三轴稳定时，均假设未失效的两个飞轮其转轴所在的二维平面与航天器本体的某个惯量主轴方向垂直，此时在系统总角动量为零的条件下，可以得出欠驱动轴的角速度始终为零，不需要控制，从而将问题简化.然而，对于“三正交加斜装”反作用轮系统，当本体轴上两个飞轮失效时，在系统总角动量为零的条件下，航天器本体任一轴的角速度均不恒为零，因此需单独进行研究.

为此，本文针对“三正交加斜装”反作用轮系统，研究当本体轴上的某两个飞轮失效时，航天器的三轴姿态稳定问题.针对系统的惯量矩阵为对角阵的情况，在系统初始角动量为零的假设下，设计分段解耦控制律，实现了三轴姿态稳定.该方法经过6次机动，可实现姿态稳定.

1 姿态运动模型

考虑下图1所示的“三正交加斜装”反作用轮系统，其中，三个飞轮的角动量与星体主惯量轴平行，第四个飞轮安装在与星体三个主惯量轴成等角的方向上，即

假设本体轴沿星体主惯量轴方向.在本体系中，飞轮系统相对星体的角动量h为

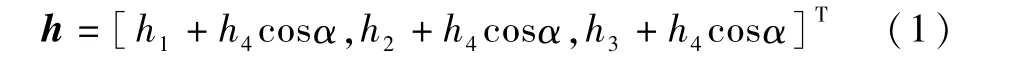
其中，hi=Iωiωsi，i=1，2，3，4.hi，Iωi，ωsi分别为第i个飞轮相对星体的角动量大小、沿轴向的转动惯量、相对星体的转动角速度.

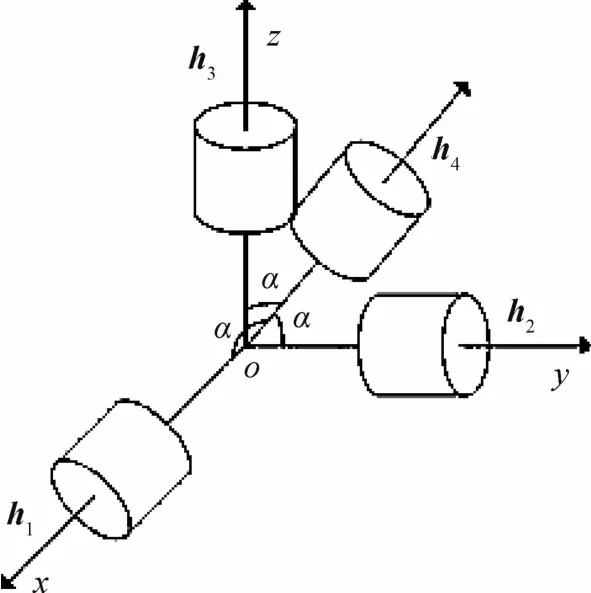
图1 “三正交加斜装”反作用轮系统Fig.1 Reaction wheel system with three orthogonally reaction wheels plus a skewed one

下面推导欠驱动航天器的姿态运动模型.

1.1 动力学方程

由航天器星体和飞轮组成的系统，假设不受外力矩，则姿态动力学方程为

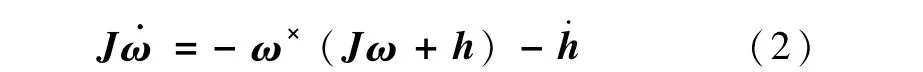
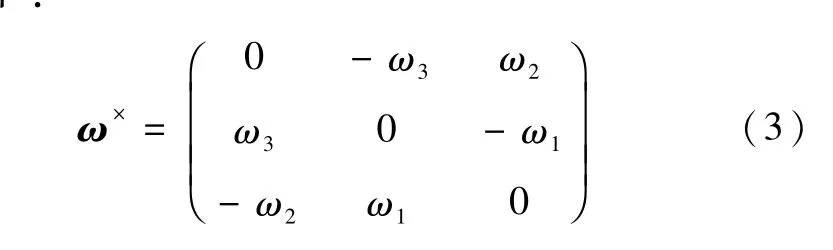
根据Crouch[3]的研究成果，为使航天器姿态可控，假设系统初始角动量为零，即

将式(4)代入式(2)中，得

将式(1)代入式(5)，并将式(5)写成分量形式

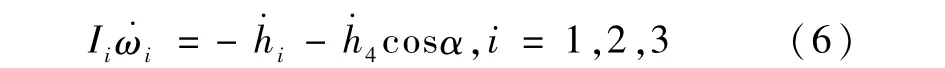
不失一般性，假设俯仰、偏航轴上的飞轮失效，因此

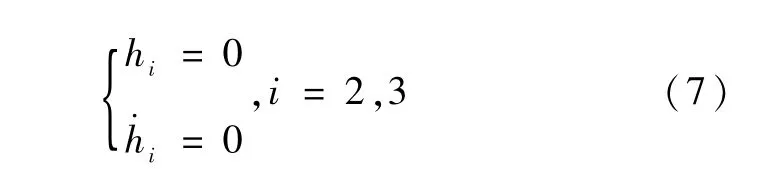
将式(7)代入式(6)中，得

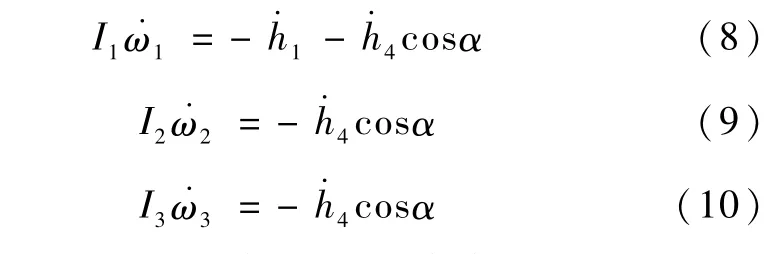
式(8)～(10)为欠驱动航天器的姿态动力学方程.

将式(1)、(7)代入式(4)，并将式(4)写成分量形式，得

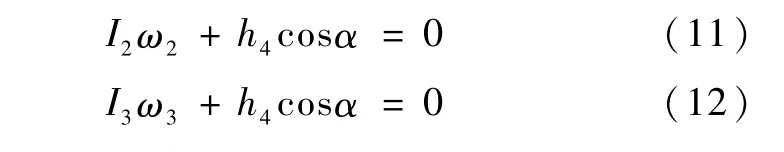
联立式(11)、(12)，得

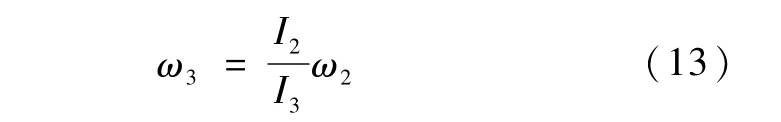
因此，ω3和ω2始终成正比例关系，如果能将 ω2镇定，则ω3也镇定.于是，此种情况下，式(10)是冗余的，只需考虑式(8)、(9).

令

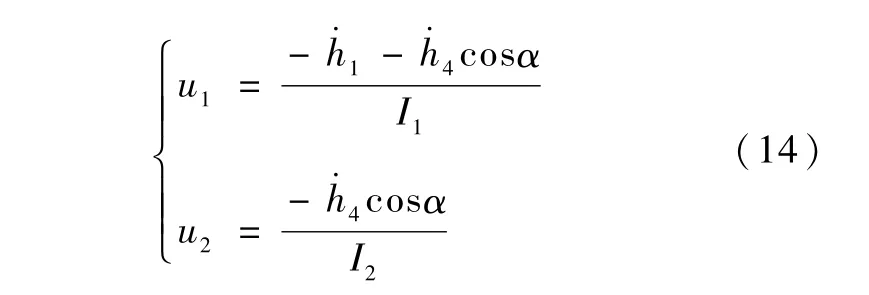
式(8)、(9)可变形为1.2 运动学方程

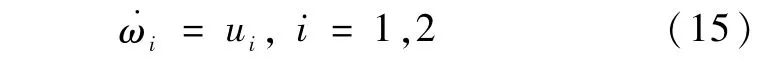
采用3-2-1欧拉角描述航天器相对惯性系的姿态，其运动学方程为

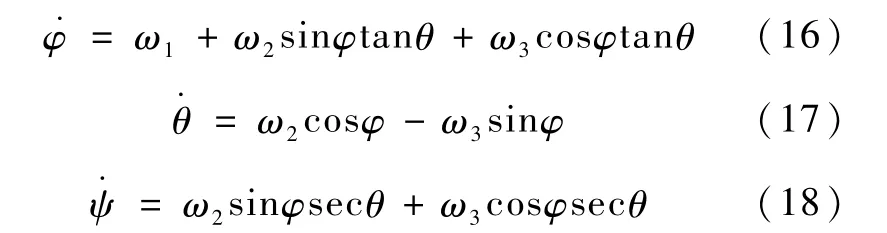
其中，φ，θ，ψ分别表示航天器相对惯性系的滚动角、俯仰角和偏航角.

将式(13)代入式(16)～(18)，得

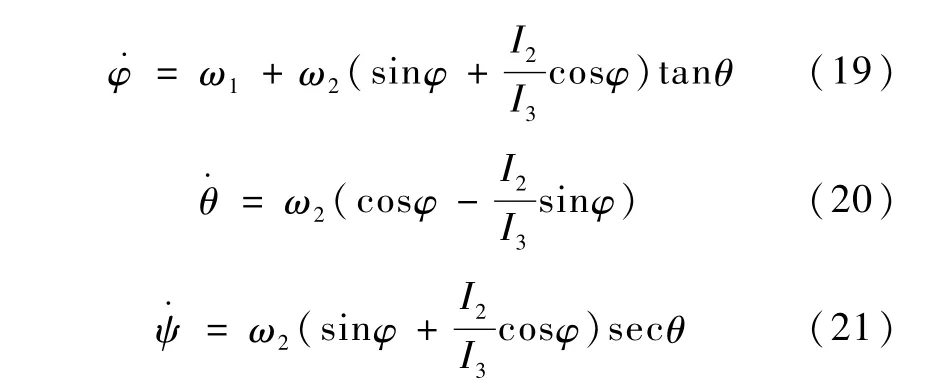
式(19)～(21)为欠驱动航天器的姿态运动学方程.

2 控制器设计

系统的姿态运动模型为式(15)、(19)～(21).观察式(19)～(21)，可以发现，如果能将 ω2镇定，滚动角φ就可以只通过 ω1(进而 u1)进行有效控制.而且，当滚动角φ满足或者时，俯仰角θ与偏航角ψ呈解耦状态，因而可以通过ω2(进而 u2)对两者实现解耦控制.下面进行详细阐述.

首先，给出如下引理.

引理1. 考虑二阶线性系统

其中，c为任意给定的非零常数.

设k＞0为任意给定正数，则控制律

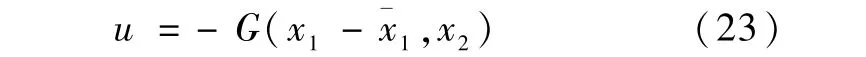
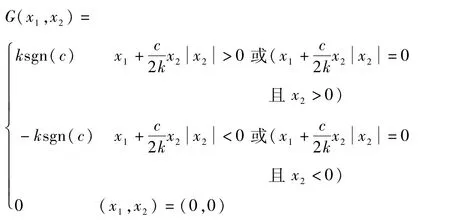
sgn(ω)为符号函数，表达式如下

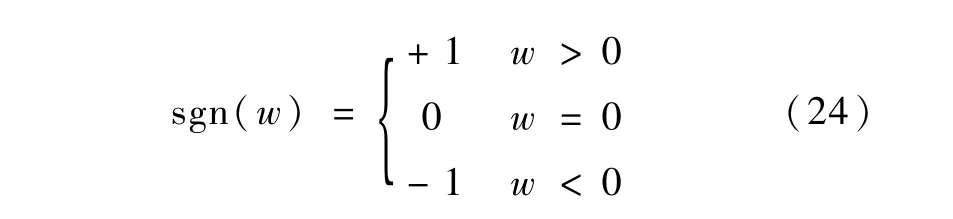
假设系统的状态变量为:χ=(ω1，ω2，φ，θ，ψ)T，则6次机动如下:

(1)状态从(ω1，ω2，φ，θ，ψ)T转移到(0，0，φ′，θ′，ψ′)T

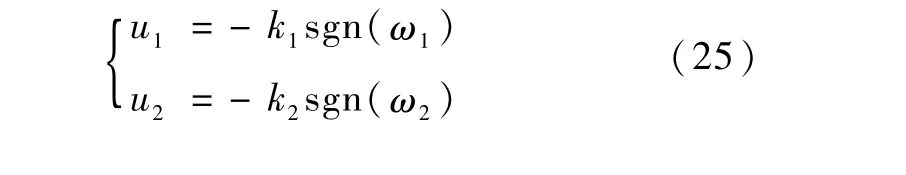
此阶段，控制律如下:其中，ki＞0，i=1，2，sgn(·)如式(24)所示.

将式(25)代入式(15)，可知有限时间内 ω1，ω2镇定.再根据式(13)，可知ω3也镇定.因此，有限时间内航天器到达静止姿态.

观察式(20)，它是非线性方程，不利于通过 ω2(进而u2)将θ稳定到零.为了把它变成线性方程，只需要使φ恒等于某个值φ*即可.将φ=φ*代入式(19)，并假设ω1=0，得

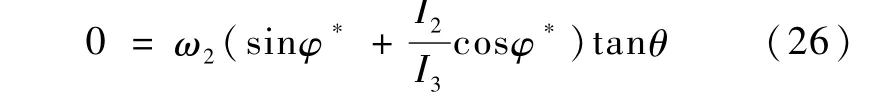
由于ω2，θ为变量，所以

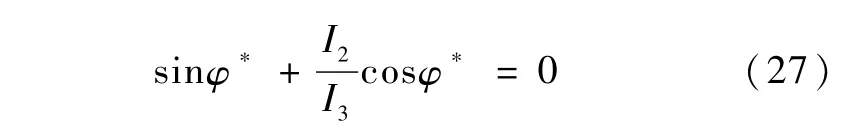
由此，可设计下面的(2)～(3)两次机动，其中第(2)次机动，使φ转移到φ*，为下一次机动做准备.第(3)次机动，使θ转移到零点.具体如下.

(2) 状态由 (0，0，φ′，θ′，ψ′)T转移到 (0，0，φ*，θ′，ψ′)T

此阶段，控制目标是:仅通过 ω1(进而 u1)的作用，使φ有限时间内转移到φ*点.为此，令u2=0.由于u2=0，根据式(15)，得 ˙ω2=0，因此ω2=0.将

(3)状态由 (0，0，φ*，θ′，ψ′)T转移到 (0，0，φ*，0，ψ′)T

此阶段控制目标是:仅通过 ω2(进而 u2)的作用，使θ有限时间内转移到零点.为此，令u1=0.由于u1=0，根据式(15)，得 ˙ω1=0，因此ω1=0.将其代入式(19)，得

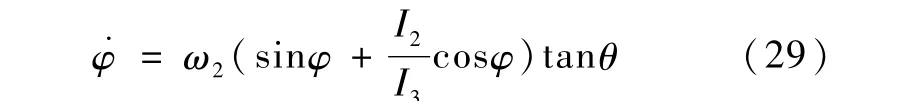
由于φ的初始值φ*满足式(27)，可以证明:此阶段(即u1=0，仅 u2作用)，航天器姿态角 φ，θ，ψ中，φ=φ*，ψ=ψ′保持不变(证明见注2).将φ=φ*代入式(20)，得

将式(30)与式(15)联立，得

令u2=-G(θ，ω2，c).由引理1知，有限时间内θ，ω2从初始状态(θ′，0)T转移到(0，0)T点.

注2. 第3次机动开始时，φ=φ*，对应姿态如图2所示.

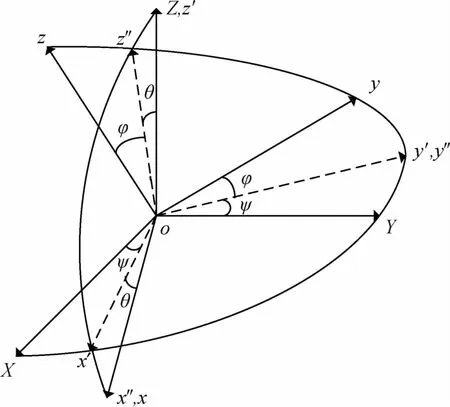
图2 第3次机动开始时航天器的初始姿态Fig.2 Spacecraft initial attitude at the beginning of the third maneuver

第3次机动过程中，始终有 ω1=0.为了利用ω2和ω3将俯仰角 θ稳定到零，同时不改变 φ，ψ的值，通过分析，可知当航天器绕 y′轴转动，即航天器角速度方向沿y′轴时，φ、ψ保持不变.根据式(13)以及ω1=0，可知航天器角速度ω位于本体系yoz平面，且与y轴夹角β满足因此，为使航天器角速度ω沿y′方向，滚动角φ应取φ*= -β，所以即为式(27).因此，第3次机动过程正确.

由于 θ已经到达零点，因此，在利用 ω2(进而u2)将ψ稳定到零点的过程中，应该使 θ保持 θ=0不变.观察式(20)，可以发现，只要将 φ稳定到φ**即可，其中φ**满足

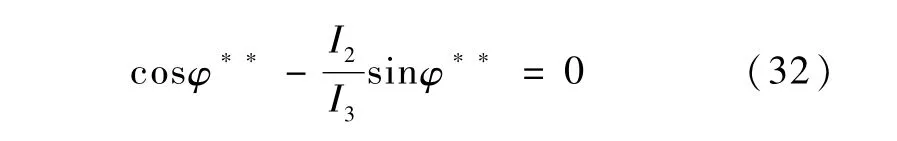
(4) 状态由 (0，0，φ*，0，ψ′)T转移到 (0，0，φ**，0，ψ′)T

此阶段控制目标是:仅通过 ω1(进而 u1)的作用，使φ有限时间内转移到φ**点.为此，令u2=0.由于u2=0，根据式(15)，得 ˙ω2=0，因此ω2=0.将其代入式(19)～(21)，得=0，=0，所以 θ，ψ保持不变，而φ满足=ω1.将其与式(15)联立，得

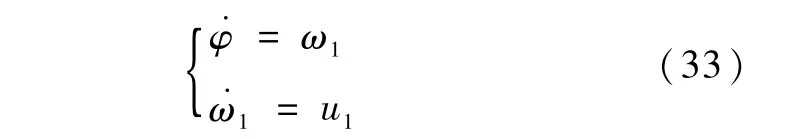
令u1=-G(φ-φ**，ω1，1).由引理1知，有限时间内φ，ω1从初始状态(φ*，0)T转移到(φ**，0)T.

(5)状态由 (0，0，φ**，0，ψ′)T转移到 (0，0，φ**，0，0)T

此阶段控制目标是:仅通过 ω2(进而 u2)的作用，使ψ有限时间内到达零点.为此，令u1=0.由于u1=0，根据式(15)，得=0，所以ω1=0.将其代入式(19)，式(19)变为

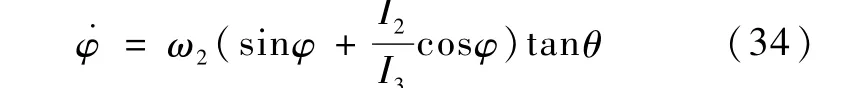
将其与式(20)联立，得

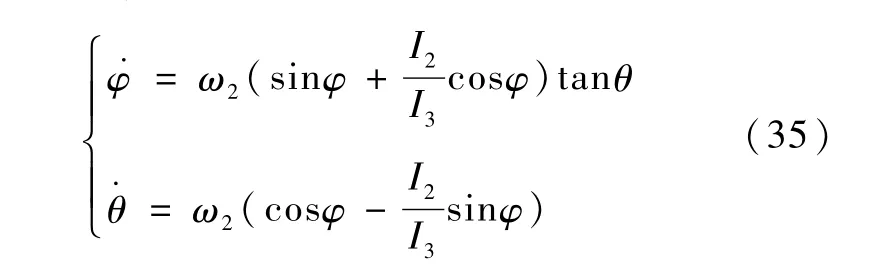
由于φ的初始值 φ**满足式(32)，可以证明:此阶段(即 u1=0，仅 u2作用)，航天器姿态角 φ，θ，ψ中，φ=φ**，θ=0保持不变(证明见注3).将φ= φ**，θ=0代入式(21)，并与式(15)联立，得

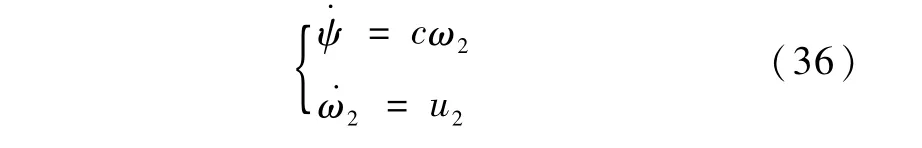
令u2=-G(ψ，ω2，c).由引理1知，有限时间内ψ，ω2从初始状态(ψ′，0)T转移到(0，0)T.

注3.第5次机动开始时，θ=0，对应姿态如图3所示.

第5次机动过程中，始终有ω1=0.由于θ已经到达目标值θ=0，因此在利用ω2和ω3将偏航角ψ稳定到零的过程中，应不改变 θ，φ的值.通过分析可知，当航天器绕 Z轴转动，即航天器角速度 ω沿Z轴时，θ，φ保持不变.由图3可知，滚动角φ取即所以即为式(32)，因此，第5次机动过程正确.

图3 第5次机动开始时航天器的初始姿态Fig.3 Spacecraft initial attitude at the beginning of the fifth maneuver

至此，航天器姿态x=(ω1，ω2，φ，θ，ψ)T已经从任意初始姿态转移到 (0，0，φ**，0，0)T.三轴姿态角φ，θ，ψ中，只有φ还没有到达零点.因此，只需要将φ从φ**转移到零点即可.由此，设计第(6)次机动.

(6)状态由 (0，0，φ**，0，0)T转移到 (0，0，0，0，0)T

此阶段控制目标是:仅通过 ω1(进而 u1)的作用，使φ有限时间内到达零点.为此，令u2=0.由于u2=0，根据式(15)，得=0，因此ω2=0.将其代入式(19)～(21)，得=0，ψ·=0，所以 θ，ψ保持

令u1=-G(φ，ω1，1).由引理1，有限时间内φ，ω1从初始状态(φ**，0)T转移到(0，0)T.

综上所述，经过6次机动控制，可使航天器姿态x=(ω1，ω2，φ，θ，ψ)T有限时间内转移到(0，0，0，0，0)T.由于ω2=0，根据式(13)，得ω3=0.因此，航天器终态时ω1=ω2=ω3=φ=θ=ψ=0，到达三轴稳定姿态.不变，而φ满足=ω1.将其与式(15)联立，得

3 数值仿真

为了验证上述方法的有效性，下面进行数值仿真.

仿真结果如图4～图6所示.

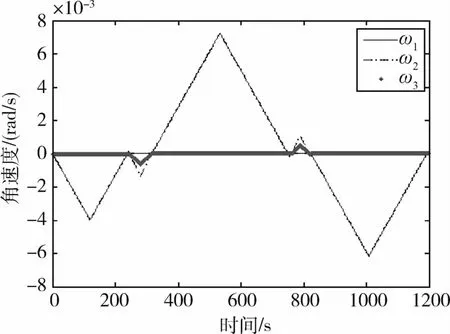
图4 角速度Fig.4 Angular velocities

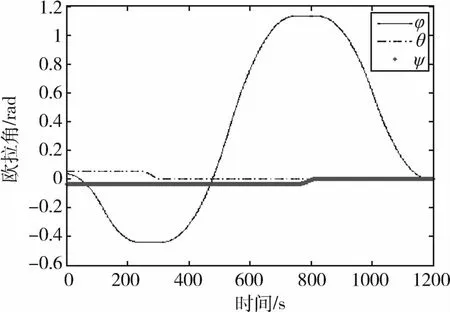
图5 欧拉角Fig.5 Euler angles

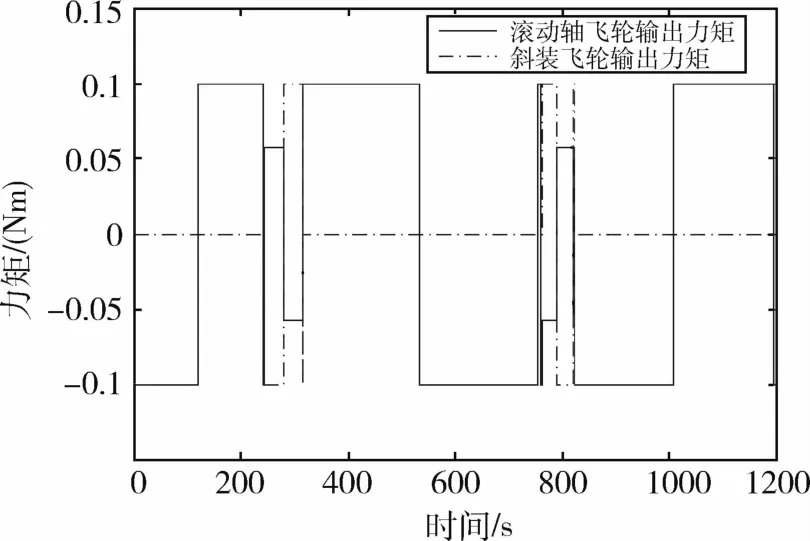
图6 控制力矩Fig.6 Control torques

图4、图5分别表示欠驱动航天器的角速度和姿态角的仿真曲线，图6表示两个飞轮的输出力矩.由图可以看出，该控制律可以实现姿态稳定，从而验证了该控制算法的有效性.

4 结 论

本文针对“三正交加斜装”反作用轮系统，研究某两个本体轴上的飞轮失效时，航天器的三轴姿态稳定问题.针对系统的惯量矩阵为对角阵的情况，在系统初始角动量为零的假设下，设计了分段解耦控制律.该方法物理意义明确，可在有限时间内使航天器从任意初始状态到达三轴稳定，完全不受欧拉角奇异的影响.同时，通过合理选择控制器参数，可将力矩控制在较小的范围.

[1] Brockett RW.Asymptotic stability and feedback stabilization[J].Differential Geometric Control Theory，1985，6(1):181-208

[2] 王芳，张洪华.欠驱动刚性航天器旋转轴稳定研究[J].宇航学报，2007，28(5):1133-1137 Wang F，Zhang H H.Spin-axis stabilization of underactuated rigid spacecraft[J].Journal of Astronautics，2007，28(5):1133-1137

[3] Crouch P E.Spacecraft attitude control and stabilization:applications of geometric control theory to rigid body models[J].IEEE Transactions on Automatic Control，1984，29(4):321-331

[4] Byrnes C I，Isodori A.On the stabilization of rigid spacecraft[J].Automatica，1991，27(1):87-95

[5] Krishnan H，Reyhanoglu M，McClam roch H.Attitude stabilization of a rigid spacecraft using gas jet actuators operating in a failure mode[C].The 31stConference on Decision and Control，Tucson，Arizona，December，1992

[6] Walsh G C，Montgomery R，Sastry S S.Orientation control of the dynamic satellite[C].The American Control Conference，Baltimore，Maryland，June，1994

[7] Morin P，Saman C，Pomet J，et al.Time-varying feedback stabilization of the attitude of a rigid spacecraftwith two controls[J].Systems and Control Letters，1995，25 (4):375-385

[8] Tsiotras P，Corless M，Longuski JM.A novel approach to the attitude control of axisymmetric spacecraft[J]. Automatica，1995，31(8):1099-1112

[9] Tsiotras P，Luo J.Reduced effort control laws for underactuated rigid spacecraft[J].Journal of Guidance，Control，and Dynamics，1997，20(6):1089-1095

[10] 黄兴宏，徐世杰.欠驱动航天器的分段解耦姿态控制[J].宇航学报，2007，28(3):531-534Huang X H，Xu S J.Attitude control of an underactuated spacecraft based on piecewise decoup ling method [J].Journal of Astronautics，2007，28(3):531-534

[11] Casagrande D，Astolfi A，Parisini T.Global asymptotic stabilization of the attitude and the angular rates of an underactuated non-symmetric rigid body[J].Automatica，2008，44(7):1781-1789

[12] Krishnan H，Reyhanoglu M，McClamroch H.Attitude stabilization of a rigid spacecraft using two momentum wheel actuators[J].Journal of Guidance，Control and Dynamics，1995，18(2):256-263

[13] Kim S，Kim Y.Spin-axis stabilization of a rigid spacecraft using two reaction wheels[J].Journal of Guidance，Control，and Dynamics，2001，24(5):1046-1049

[14] Horri N M，Hodgart S.Attitude stabilization of an underactuated satellite using two wheels[C].The 2003 IEEE Conference on Aerospace，Los Angeles，March，2003

[15] 阳洪，吴忠.基于飞轮的欠驱动航天器姿态控制器设计[J].控制理论与应用，2008，25(3):506-510 Yang H，Wu Z.An attitude controller for under-actuated spacecraft with two flywheels[J].Control Theory and Applications，2008，25(3):506-510

[16] 金磊，徐世杰.带有两个飞轮的欠驱动航天器姿态稳定控制研究[J].中国空间科学技术，2009，29(2):8-16 Jin L，Xu S J.Attitude stabilization of an underactuated spacecraft with two reaction wheels[J].Chinese Space Science and Technology，2009，29(2):8-16

[17] Yang H，Wu Z.Attitude controller design of underactuated spacecraftwith two controlmoment gyroscopes[C]. The 6thWorld Congress on Intelligent Control and Automation，Dalian，June，2006

[18] Han C，Pechev A N.Underactuated satellite attitude control with two parallel CMGs[C].2007 IEEE International Conference on Control and Automation，Guangzhou，May，2007

[19] Mehrabian A R，Tafazoli S，Khorasani K.On the attitude recovery of an underactuated spacecraft using two controlmoment gyroscopes[C].Joint48thIEEE Conference on Decision and Control and 28thChinese Control Conference，Shanghai，December，2009

[20] 章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社，1998 Zhang R W.Spacecraft orbit and attitude dynamics and control[M].Beijing:Beijing University of Aeronautics and Astronautics Press，1998

Design of A ttitude Controller for W heel Controlled Underactuated Rigid Spacecraft under Failure of Two O rthogonalW heels

LIGongjun1，2
(1.Beijing Institute of Control Engineering，Beijing 100190，China; 2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China)

For a spacecraft with three orthogonally placed reaction wheels and the fourth skewed one，the attitude control problem is considered in this paper when two of three orthogonally placed wheels failed. Under the assumption of zero system angular momentum，a piecewise decoupling control law is designed to stabilize the attitude of the spacecraft by using two residual wheels.By using the Euler angle parameterization method，spacecraft dynamics and kinematics are given and a piecewise control law is proposed based on the decoupling property of the model.After six maneuvers，the proposed scheme ultimately guarantees the attitude stability.Simulation results demonstrate the proposed control approach.

underactuated;spacecraft;attitude stabilization;decoupling control;reaction wheel

V448.2

A

1674-1579(2012)03-0021-06

10.3969/j.issn.1674-1579.2012.03.005

李公军(1984—)，男，硕士研究生，研究方向为欠驱动航天器的控制.

2011-10-30