轮系航天器的角动量包络分析及角动量管理

，

1. 北京控制工程研究所，北京 100094 2. 空间智能控制技术重点实验室，北京 100094

反作用轮由于高精度连续方式输出力矩，因此广泛地作为航天器姿态控制系统的执行机构。为实现三轴姿态控制以及满足角动量需求且具有一定冗余，一般配置4个或以上飞轮组成轮系系统输出控制力矩[1-2]。航天器在轨运行时受环境外扰力矩作用，当无角动量卸载介入时轮系积累角动量将持续增长，使得飞轮组角动量饱和而丧失三轴控制能力。因此，系统一般配置磁卸载或喷气卸载装置[3]，特别是当判定飞轮角动量超过设定安全阈值时自主触发喷气卸载。然而，喷气卸载势必引起星体姿态波动对载荷工作产生影响，因此合理的系统设计，并辅之有效的角动量管理以减小不必要喷气卸载，是在轨航天器实现载荷长时间连续工作的重要手段。

对于轮系航天器控制系统，轮系角动量包络分析是轮系构型、飞轮容量选择及角动量管理[3-4]，乃至轮系可重构性分析[5]等的先决条件。文献[6]对飞轮角动量包络研究首次阐述了实际最大角动量和伪逆解可达角动量两类角动量包络概念，利用几何方法分析对比了几种典型飞轮构型的两类角动量包络情况，并给出了一种斜装飞轮系统基于伪逆解可达角动量包络的卸载方案。文献[7]针对同类型的三飞轮及四飞轮系统可能存在的不同构型，从最小能耗角度分析合适的安装方式。

针对现常用能量最优的伪逆力矩分配方法未能充分利用轮系角动量和力矩的问题，相关研究[8-10]基于角动量与力矩包络分析及新型优化力矩分配方法进行研究。Markley等基于几何方法对各种构型的最大力矩及最大角动量包络分析，并将包络面分成与飞轮状态相关的多区域，通过判定期望力矩所属区域而采用预先按区域设定的不同L∞力矩分配阵进行力矩分配，以发挥轮系最大能力[8]。针对Markley给出包络确定及解算效率，Yoon等采用包络面上飞轮饱和状态的角动量包络及力矩包络描述方式，结合包络分析开展适应姿态机动的构型优化，并改进L∞力矩分配算法[9]。郭延宁等主要研究了航天器姿控系统中冗余飞轮构型的力矩分配问题，给出了能量最优的力矩分配策略,基于静态最优化理论和轮系性质设计了相应的力矩最优分配策略,以有效地输出飞轮系的最大力矩[10]。

角动量喷气卸载除了需消耗有限的工质外，还可能对卫星轨道产生影响[11]，因此如何避免在特定力矩分配下系统角动量在达到包络面之前出现飞轮角动量饱和而触发不必要动量卸载的问题，一直是高轨航天器控制系统设计中需要格外关注的问题。针对既定任意冗余轮系构型航天器，本文基于可视化角动量包络分析及合适角动量包络特征参数描述选取研究，提出结合伪逆与基于目标角动量的零运动动态调整相结合的力矩分配方法，使得系统可充分利用实际最大角动量包络，且适合航天器在轨实时有效的角动量管理。

1 轮系角动量包络分析

考虑任意两飞轮安装不平行的N(N≥3)个飞轮所组成轮系，飞轮i(i=1,2,…,N)安装方向hw,i∈R3为单位向量，对应角动量Hw,i∈R满足如下约束：

式中：Hmin ,i与Hmax ,i为飞轮角动量最小值与最大值，当采用同类飞轮时一般有Hmax ,i=-Hmin ,i>0。

记角动量向量为：

轮系合成角动量可表示为:

对于星体坐标系下的任意单位向量

可使得S为：

记HΣ为轮系合成角动量HΣ在S方向的投影，则有

上式两边左乘矩阵C，有

式(6)可分解为如下两部分：

求轮系组合沿星体S方向的最大合成角动量问题,即为在不等式(1)和等式(7)约束下的线性规划问题:

以4个角动量相同的飞轮所组成的如图1所示金字塔构型为例，飞轮角动量单位化且满足-1≤Hw,i≤1(i=1,2,3，4)，各飞轮安装方向为：

hw，1=[ 0.8165408118 0 0.5772877121 ]T

hw，2=[ 0 0.8165408118 0.5772877121 ]T

hw，3=[ -0.8165408118 0 0.5772877121 ]T

hw，4=[ 0 -0.8165408118 0.5772877121]T

对上述线性优化问题求解，可求得各飞轮角动量满足Hmax ,i=-Hmin ,i=1 N·m·s条件下的轮系角动量包络，如图2所示。由可视化包络图可知轮系角动量包络为十二面体，即包络面由12个平面四边形所围成的封闭面。

综合轮系合成角动量在可视化包络面所对应的各飞轮角动量值可直观地表现出角动量包络的相关性质[8]：轮系合成角动量可看作由N维超立方体映射到三维空间的多面体，该多面体由顶点、边和面组成，其中顶点为所有飞轮饱和角动量合成，各边为除一个飞轮外其余飞轮均饱和下的角动量合成，面为除两飞轮外其余飞轮均饱和下的角动量合成。

2 基于包络面可视化的轮系角动 量分析

根据每个飞轮角动量约束条件式(1)的紧集特性可得Hw,i为凸集，进一步根据凸集相关性质[10]可得飞轮角动量包络面的相关性质：轮系合成角动量HΣ为各个飞轮角动量Hw,i的线性组合，根据凸集之和为凸集的性质可知系统合成角动量HΣ形成的动量体也为凸集。另外，由于空间平面为凸集，于是根据凸集交集为凸集的性质可知角动量体外包络平面多边形为凸多边形。

对于任意两飞轮，不妨记为k与l，当其他N-2个飞轮角动量均处于饱和，Hw,k与Hw,l在其范围内变化时所对应轮系合成角动量变化范围为一个平行四边形区域，其法线为n=hw,k×hw,l/‖hw,k×hw,l‖，且两边分别与hw,k和hw,l平行(文中‖·‖均为2-范数，表示向量长度)。当N-2个饱和飞轮的合成角动量在法线n上投影达到最大(或最小)时所对应平行四边形则在轮系角动量包络上，不妨记为Π:A1A2A3A4，如图3所示，4个顶点按平面法线n(取为外法线)右手螺旋依次为A1～A4，Ai坐标为(xiyizi)。对于N个飞轮组成轮系，由任意两飞轮组合可得包络上平行四边形数为N(N-1)。

由多边形Π的任意第i个顶点Ai为起点，与其相邻两顶点Ai+1、Ai-1为终点，可形成两个向量Ai，i+1与Ai，i-1(当i=4时为A4,1与A4,3)。由其中任意两相邻向量可求得平面Π的外法线n为：

结合任意一顶点Ai，可得Π所在平面的方程为：

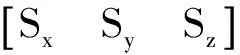
x=Sxd，y=Syd，z=Szd(11)

式中：d为参量。

将直线方程各坐标系分量代入式(10)可得关于参量d的方程为：

nx(Sxd-xi)+ny(Syd-yi)+

且当nTS≠0时，其解为：

式中：AO，1为以原点O为起点、顶点A1为终点的向量。当d>0时意味着直线由原点沿单位向量S与四边形Π所在平面存在交点，且向量B=d·S。

当判定沿单位向量S与平面四边形Π所在平面存在相交点后，可进一步依据平面凸多边形内点判断方法[14]直接导出的沿方向S与包络面上平面四边形Π的交点存在性判据进行判断。

交点存在性判据：若式(12)存在参量d大于零的解，且对于平面四边形Π各边均满足如下不等式：

式中：Ai,B为以顶点Ai为起点、以交点B为终点的向量，i=1,2,3,4。则沿S方向与轮系角动量包络面的四边形Π存在交点B，当有等号成立时则交点B为Π边上的点；否则与平面四边形Π不相交。

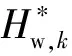
由前可知，根据N飞轮组的轮系角动量包络面由包络多面体的其中4个顶点围成的p=N(N-1)个平行四边形Πυ(υ=1,2，…,p)区域所组成，并且当已知各平行四边形Πυ内飞轮角动量饱和状态即可求包络面各点处对应飞轮极限角动量，因此采用如下3个包络特征参量集的定义可对轮系角动量包络进行描述：

1){Πυ:υ∈{1,2，…,p}}；

2)Πυ的有序顶点集{Λυ,j:j∈{1,2，3,4}}；

3) 包络面上飞轮饱和状态{Υυ,k:k∈{1,

2，…,N}}

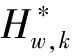
注1：由于不同平面四边形可能存在公共顶点，在具体实现上为减小存贮量可按一定编号存储角动量包络多面体顶点坐标，Πυ的顶点集各坐标可按索引方式获取；当Hmax ,i=-Hmin ,i时，由式(2)有HΣ(-Hw)=-HΣ(Hw)，即包络面上任一平行四边形均存在与之原点对称的平行四边形，因而该情况下仅存贮一半数目平行四边形的相关信息即可。

注2：为减少计算量，由可视化包络可得合成角动量最大幅值HΣmax，当式(13)的解满足0≤d≤HΣmax时才执行后续交点存在性判断，否则直接判定该交点不在当前平行四边形内。

以第1节的金字塔飞轮组合构型，由图2所示可视化角动量包络可得其12个面的包络特征参数如表1所示。对于指定单位方向

按本节给出的过程可求得沿S方向与包络面相交点在平行四边形Π2内，且此处对应各飞轮角动量分别为1.00，1.00，-0.09和0.51，与由式(8)优化求解结果一致。

表1 金字塔构型的动量包络面特征参数Table 1 Characteristic parameters of momentum envelope for RWs in pyramid array

3 轮系航天器的角动量管理

已知星体相对参考系的姿态误差四元数Δq(t)和角速度误差Δω(t)，类似文献[15]可采用如下姿态控制律:

τc=KpΔq+KdΔω+ω×(Jsω+HΣ)

(15)

式中：Js∈R3×3为星体的转动惯量；ω∈R3为星体角速度，ω×∈R3×3为ω的反对称阵；控制系数阵Kp、Kd∈R3×3为正定矩阵。

假设N个飞轮组的当前角动量向量为Hw，且设定的飞轮偏置标称角动量向量为Hw0∈RN。不失一般性，假设CwHw0=0，则轮系角动量与合成标称角动量的偏差为:

HΣ=CwHw

随着外扰作用，轮系合成角动量幅值逐步增大直至达到角动量包络面。当‖HΣ‖≠0时，根据轮系合成角动量实时设定单位向量

S=HΣ/‖HΣ‖

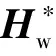
对于由姿态控制律得到的期望控制力矩τc，在伪逆分配律[16]基础上引入角动量自主调节，得到如下飞轮力矩分配律:

(16)

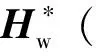
为对式(16)中所引入的角动量自调整策略特性进行分析，过程中基于如下几点考虑：

1)空间环境扰动力矩幅值一般均很小，且在短时间内角动量积累量可忽略；

基于上述考虑，在航天器姿态稳定时由式(16)可得：

2)对于由特征值0对应特征向量v0,1，v0,2，v0,3与特征值1对应特征向量v1,1，v1,2，…，v1,N-3所组成的所有特征向量中任意两者互为正交。

根据上述结论，对于初始时刻t0飞轮角动量Hw(t0)与沿S方向极限角动量的偏差ΔHw(t0)可表示为：

(18)

式(18)右端第一项为常数项，第二项为指数衰减项，并且kNull为ΔHw(t)沿v11，… ，v1,N-3方向指数衰减系数，通过调整该值可改变飞轮角动量调整的动态特性。

CwHw(t)=CwHw(t0)

于是有

即ΔHΣ(t)由角动量包络上特定点与飞轮当前系统角动量唯一确定。考虑角动量调节稳态状态，即在a1,i(t0)=0(i=1,…,N-3)时有

由此可见，上述关于a0,i(t0)(i=1,2,3)为参量的方程组式(19)的解由角动量包络上特定点与飞轮当前系统角动量唯一确定。

由式(18)形式可知，虽然增大kNull可提高飞轮角动量自调整速度，但当初值ΔHw(t0)过大时可能导致调整所需力矩过大而出现飞轮输出力矩饱和现象。为克服上述问题以及指数收敛下随ΔHw调整过程减小使得调整速度变慢问题，除综合考虑调整速度与调整力矩大小选择合适kNull值外，可对式(16)角动量调节输入ΔHw进行单位化，对应飞轮力矩分配律为：

4 仿真与分析

以运行于轨道高度为36 000 km的对地稳定卫星为例，卫星星体转动惯量为:

符号diag{·}表示对角阵。系统配置4个力矩0.1 N·m和角动量10 N·m·s飞轮，安装如图2所示金字塔组合构型。卫星采用整星零动量控制方式，飞轮初始偏置角动量为：

控制参数选取为:

施加于星体的环境外扰力矩为

为对比验证本文所提出角动量管理策略的效果，首先采用常用的伪逆力矩分配方式进行仿真分析，即设定kNull=0，仿真结果如图4和图5所示。结合图4给出的星体相对轨道系的滚动角φ、俯仰角θ及偏航角Ψ三轴姿态和图5给出的四飞轮角动量可知，轮系角动量在122 000 s到达角动量包络面之前飞轮1、飞轮2和飞轮4分别在60 000 s、80 000 s及110 000 s附近不同时间段出现角动量饱和情况，此期间使得姿态角相应地出现一定程度波动。

采用本文提出的角动量管理策略进行仿真，当设定kNull=0.01时在其他相同条件下仿真结果如图6与图7所示。结合图6给出的三轴姿态角和图7给出的四飞轮角动量可知，轮系在吸收外扰积累角动量过程中通过实时调整飞轮角动量，避免了轮系角动量在到达包络面之前出现部分飞轮角动量饱和现象且保证控制性能，至到122 000 s两飞轮角动量同时饱和，即轮系角动量达到包络面，系统失去三轴姿态控制能力。

在伪逆力矩分配方式下，即kNull=0，增大系统控制参数以分析控制能力提升对系统性能影响。选取控制参数为：

仿真结果如图8和图9所示。由图8可知星体姿态在出现飞轮角动量饱和时姿态波动相比图4有很大程度改善，但图9给出的四飞轮角动量与图5结果基本相同。由上比较可知，虽然通过提高系统反馈控制能力可有效降低飞轮角动量饱和对姿态性能影响，但对系统角动量达到角动量包络前的飞轮角动量饱和现象无任何改善作用。

通过上述仿真对比可知，采用所提出角动量管理方法可充分利用轮系角动量容纳能力，有效避免在轮系角动量积累到达角动量包络面之前出现部分飞轮饱和情况，相比常规伪逆力矩分配策略可延长高轨卫星喷气动量卸载间隔。

5 结束语

本文针对受扰轮系航天器角动量管理问题，基于飞轮系统的可视化角动量包络分析，提出了一种轮系角动量包络特征参数描述及角动量包络面处飞轮极限角动量求解方法，在此基础上给出了一种基于设定角动量目标的零运动力矩分配的角动量管理策略及其特性理论分析，对于既定轮系构型可充分利用轮系角动量空间，可使得飞轮角动量达到角动量包络面之前避免出现飞轮角动量饱和情况。充分利用轮系角动量的有效性,对所提出力矩分配策略进行了数学仿真验证。通过与常规伪逆力矩分配策略对比，结果表明该方法可有效延长角动量喷气卸载间隔，在采用喷气卸载高轨道卫星角动量管理上具有一定的优势。

References)

[1] ANDERSEN G C, QUINN D A, BEALS G A, et al. An overview of the Hubble space telescope pointing control system design and operation[C] ∥AIAA Guidance, Navigation, and Control Conference, Hilton Head Island, SC: AIAA, 1992.

[2] 黎康, 乔国栋, 刘新彦. 高分四号卫星控制方案设计特点及在轨实现[J]. 空间控制技术与应用, 2016, 42(6): 1-8.

LI K, QIAO G D, LIU X Y. Highlights of attitude and orbit control system (AOCS) for GaoFen-4 satellite with on-orbit verification [J]. Aerospace Control and Application, 2016, 42(6): 1-8(in Chinese).

[3] 屠善澄. 卫星姿态动力学与控制[M]. 北京:宇航出版社，北京:2001.

[4] 林来兴, 白拜尔. 卫星姿态控制反作用轮的最佳安装结构[J]. 自动化学报，1984, 10(3): 228-238.

LIN L X, BAI B E. The best orientation of reaction wheel in satellite attitude control[J]. Acta Automatic Sinica, 1984, 10(3):228-238(in Chinese).

[5] 顾朋，王大轶，刘成瑞. 零动量卫星轮控系统可重构设计研究[J]. 中国空间科学技术, 2013, 33(1): 7-14.

GU P, WANG D Y, LIU C R. Research on momentum wheel reconfiguration design of zero-momentum satellite [J]. Chinese Space Science and Technology, 2013, 2013, 33(1): 7-14(in Chinese).

[6] 徐帆, 林来兴. 角动量包及斜装飞轮的卸载系统[J]. 航天控制, 1986,4(1): 22-30.

XU F, LIN L X. Angular momentum envelope and unloading system of skewed flywheel system [J]. Aerospace Space Control,1986,4(1): 22-30(in Chinese).

[7] ZULIANA I, RENUGANTH V. A study of reaction wheel configurations for a 3-axis satellite attitude control[J]. Advances in Space Research, 2010, 45(5):750-759.

[8] MARKLEY F L, REYNOLDS R G, LIU F X, et al. Maximum torque and momentum envelopments for reaction wheel arrays[J]. Journal of Guidance, Navigation, and Control Conference, 2010, 33(5):1606-1614.

[9] YOON H, SEO H H, CHOI H T.Optimal uses of reaction wheels in the pyramid configuration using a new minimum infinity-norm solution[J]. Aerospace Science and Technology, 2014, 39: 109-119.

[10] 郭延宁, 马广富, 李传江. 冗余飞轮构型下力矩分配策略设计与分析[J]. 航空学报, 2010, 31(11): 2259-2265.

GUO Y, MA G F, LI C J. Design and analysis of torque allocation strategy for redundant flywheel configuration [J]. Acta Aeronautica ET Astronautic Sinica, 2011, 31(11): 2259-2265(in Chinese).

[11] 黄勇, 胡小工, 董光亮, 等. 动量轮卸载对环月卫星SMART-1卫星轨道的影响和定轨策略[J]. 飞行器测控学报, 2007, 26(5): 62-66.

HUANG Y, HU X G, DONG G L, et al. The effect of wheel off-loading on the orbit of lunar satellite SMART-1[J]. Journal of Spacecraft TT&C Technology, 2007, 26(5): 62-66(in Chinese).

[12] 赖炎连, 贺国平. 最优化方法[M]. 北京:清华大学出版社, 2008:161-216.

[13] 张德丰. Matlab数值分析与应用[M]. 北京:国防工业出版社, 2007:256-260.

[14] 郭雷,王洵,王晓蒲. 有向回路法和网格法:多边形内外点判别的新算法 [J]. 计算机工程与应用, 2002,38(19):119-122.

GUO L, WANG X, WANG X P.Directed-loop method and grid method: new algorithms for inclusion test of planar polygons[J]. Computer Engineering and Application, 2002, 38(19):119-122(in Chinese).

[15] 韦娟, 宁方立. 误差四元数及其在航天器姿态控制中的应用[J]. 飞行力学, 2006, 24(2):60-68.

WEI J, NING F L. Error quaternion and its application of attitude control for a spacecraft[J]. Flight Dynamics, 2006, 24(2):60-68(in Chinese).

[16] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京:北京航空航天大学出版社, 1998:273-276.