半球谐振陀螺力反馈控制回路设计

陈小娟，李 恺，王德钊，李 东

(北京控制工程研究所，北京100190)

技术交流

半球谐振陀螺力反馈控制回路设计

陈小娟，李 恺，王德钊，李 东

(北京控制工程研究所，北京100190)

阐述半球谐振陀螺(HRG)的基本组成和控制原理，详细给出其核心控制回路即力矩再平衡控制回路的频率特性设计过程和电路实现.仿真试验结果表明了该方法的有效性.

半球谐振陀螺;力矩再平衡控制回路;频率特性

半球谐振陀螺(HRG)是一种小尺寸、极长寿命和极高可靠性的高精度固态陀螺[1].通过控制回路和电子线路的综合设计，即可充分发挥HRG的上述特征[2].

HRG可在两种不同的模式下工作:第一种模式为全角模式，在这种模式下，陀螺类似于速率积分陀螺，具有动态范围大、频带宽的特点.另一模式为力再平衡或力反馈模式，在全角模式的基础上通过改变控制规律使陀螺工作在速率陀螺状态下，这种模式具有高的角度分辨率[3].对空间定位和控制应用而言，一般要求HRG工作在力反馈模式下.

1 HRG控制原理[4]

HRG属于Coriolis类陀螺，其工作原理是基于半球谐振子的谐振驻波对惯性转动敏感这一特性.陀螺的主要功能部分组成为:半球谐振子、力矩器、信号器.这3部分均由石英材料制成.谐振子作为旋转敏感要素被定位在力矩器和信号器之间，三者之间均有间隙以隔离彼此间的表面.这些石英件表面均被金属化从而在谐振子、力矩器、信号器之间形成电容器.这些电容器被用作电容读出器和谐振子静电控制.由于半球谐振子、力矩器、信号器被结合在一起并密封在一个真空室内，因此陀螺工作在真空状态.另外，一个缓冲放大器电路被固定在密封的真空室内以放大电容信号器的信号.

为了使半球谐振陀螺作为一个角速率测量部件，需要利用相位锁定环来跟踪自然谐振频率;幅值控制环来维持和控制标称谐振挠性振幅;正交控制环来控制振动波形的形状;速度控制环(力矩再平衡控制环)实现输入角速度测量.在这4条控制回路中，力矩再平衡控制回路是核心，该回路的性能设计直接影响陀螺的动、静态特性.力反馈控制回路的基本结构如图1所示.

根据陀螺线路的组成，确定各部分的传递函数:

解调滤波环节:

乘法器环节:K2;

高压施力器环节:K3.

另外，陀螺头部的传递函数[5]将通过试验方法确定;校正环节将是需要设计的环节.通过校正环节的合理设计以满足闭环系统的动、静态指标要求.

图1 力矩再平衡控制回路结构框图Fig.1 Moment rebalance control loop block diagram

2 校正环节设计

根据卫星应用对陀螺通频带的要求，为了提高系统的静态刚度，可选用带积分环节的校正环.同时，为了确保系统具有良好的动态品质，应根据已知环节的参数，再加入适当的超前/滞后校正.因此，选定力反馈控制回路的设计目标开环传递函数:截止频率ωc=100 rad/s左右;且在截止频率左、右各展宽5倍频程范围内，幅频特性为-20dB/10倍频程，这样可确保闭环系统有较好的动态品质.

2.1 陀螺头部传递函数的确定

准确地确定陀螺头部的传递函数具有重要意义，它是进行后续校正环节设计的基础.

为此，首先以两个陀螺为试验对象，进行陀螺头部传递函数试验.如图1中所示，在试验中，闭环断开点为标号3点，变频信号从1点输入，从2点测试.试验结果显示，数据重复性较好.将数据绘制成对数幅频特性曲线如2所示.

图2 HRG幅-频特性曲线Fig.2 HRG magnitude-frequency response curve

由图2分析可知:陀螺头部有一个积分环节，即陀螺头部的传递函数包含:

该结论经过对同一陀螺多次试验和对不同陀螺的试验得到验证.通过上述试验并结合工程实际经验，对半球谐振陀螺头部传递函数得出如下结论:

1)陀螺头部的传递函数中至少包含有一个积分环节;

2)陀螺头部的传递函数中可能还包含有惯性环节，但惯性环节的时间常数一定不会很大，至少在目前测试条件下无法测出.

2.2校正环节的确定

通过对现有电路与目标开环传递函数伯德图的对比，可知校正环的构成如下:

但在试验中发现:在原有电路参数下，加入积分环节后系统出现振荡，该现象通过加入微分环节也很难消除.为此，复验系统各组成环节的参数后发现，原解调滤波环节的时间常数T1=0.796s过大.因此，在加入校正环节前首先应该将该参数调小，确保在20～500rad/s频段内没有极点，通过电路阻容参数调整后，T1=0.002s.

在此基础上，加入上述校正环，以实现设计目标开环传递函数.

根据图2可知:T2=0.0005s;T3=0.0002s; T4=0.05s.

其中T3的引进，可对4.5kHz的解调噪声带来-15dB的衰减效应.根据所设计的校正参数，可计算得到该力反馈系统的相位裕度为63°，幅值裕度为22dB，保证系统有较理想的动态品质.最后，通过对闭环系统的阶跃响应试验调整开环放大系数.试验整定以后，阶跃响应结果为图3所示.

图3 阶跃响应Fig.3 Step response

由图3可看到，超调仅20%，振荡次数为1次，峰值时间为0.046s，可推断其通频带为16Hz，其动态品质令人满意.

其中T3可以根据系统的实际高频干扰信号进行调整.至此，校正环节的参数基本已被确定下来.最后，通过对系统阶跃响应的测试调整整个开环的放大倍数.

参见图1，设系统前向通道的增益为KQ，反馈通道的增益为KF，最后得到整个开环放大系数 K= KQ·KF≅2654.4，对此，可绘制出这时实际系统的开环伯德图如图4所示.

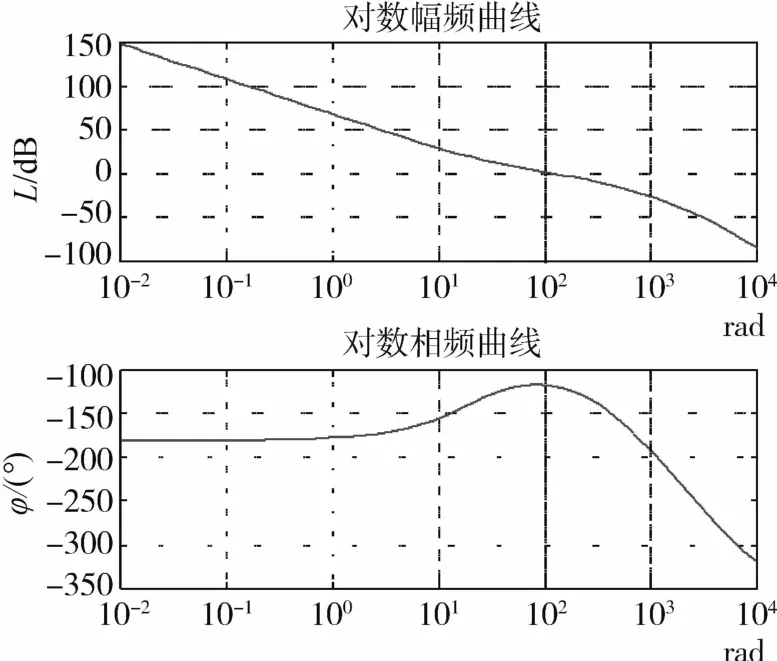
图4 系统的开环伯德图Fig.4 Open-loop bode diagram of system

系统幅值裕度与对应的频率为:Gm=12.2635; Wcg=795.2030.

系统相位裕度与对应的频率为:Pm=61.4979; Wcm=129.6554.

同时可知图1对应的系统闭环传递函数为:

3 电路设计及实验

力反馈控制回路的校正环节的电路设计如图5所示，这时力反馈控制控制系统的结构如图6所示.

系统的闭环传递函数为:

比较式(4)与式(5)可知，两闭环系统零、极点相同，因此系统稳定性相同;但增益不同，使系统快速性和动态过程消失快慢略有区别，增益可以通过改变阶跃的幅值进行补偿调整.

基于上述认识，通过所加的“输入”的幅值不同，用图6系统替代图1系统进行阶跃响应试验是可行的和有意义的.

针对上述力反馈系统开展了如下实验:

(1)时域性能指标测试

系统时域性能指标测试时，从“输入”点加入输入信号，响应信号从“输出”点测量.

图5 局部电路图Fig.5 Local circuit diagram

图6 系统组成Fig.6 Control system block diagram

系统时域性能指标测试响应曲线如图7和图8所示.

图7 不加校正环节时的响应曲线Fig.7 Time domain response without corrective loop

图8 加校正环节后的响应曲线Fig.8 Time domain response with corrective loop

对比图7和图8可知，系统没有加校正环节前，阻尼比较小，动态过程超调量大，调节时间长，平稳性差.校正环节加入后，系统超调量小，平稳性好.同时，根据对图8曲线可知tP=11ms，通过经验公式[6]计算系统带宽f≅10Hz，满足卫星使用的需求.

(2)系统频域性能测试

进行系统频域性能测试，系统闭环幅-频特性测试结果如9所示.

图9 系统闭环幅频特性Fig.9 Closed-loop magnitude-frequency characteristics of system

从闭环幅频特性曲线M(0)=1，说明系统在阶跃信号作用下没用静差.另外，幅-频特性曲线峰值Mm不大，其阶跃响应过程超调量小，平稳性好.同时，M(ω)=0.707时对应的频率约10 Hz，系统带宽满足设计要求.

4 结 论

通过对HRG力反馈模式下力矩再平衡控制回路频率特性的研究和系统时域、频域性能测试可知，系统动、静态指标满足设计要求，校正环节的设计合理、可行.本文研究成果为HRG的高精度应用打下基础.

[1] IEEE standard specification format guide and test procedure for Coriolis vibration gyros[S].IEEE Std 1431-2004

[2] 郭栓运，于集建.半球谐振陀螺的关键技术—信号闭环理论及检测电路[J].应用光学，1995，15(5):45-49 Guo Q Y，Yu J J.The unique technica-the theory of signal closed loop and test circuit[J].Journal of Applied Optics，1995，15(5):45-49

[3] M aтвеевB A，IипaтниκовBИ.，AлеxинA B. Πpоеκтиpовaние. Bолнового твеpдотелъного гиpоcκопa.И3дaтелъcтвоMΓTyимениH.Э. Бayмaнa，1998:1-83

[4] Matthews A，Bauer D A.The hemispherical resonator gyro for precision pointing app lications[J].Space Guidance，Control，and Tracking II，SPIE，1995，2466:128-139

[5] 吕志清.半球谐振陀螺(HRG)信号处理技术[J].中国惯性技术学报，2000，8(3):58-61 Lv Z Q.Signal processing technique for hemispherical resonant gyro(HRG)[J].Journal of Chinese Inertial Technology，2000，8(3):58-61

[6] 冯巧玲.自动控制原理[M].北京:北京航空航天大学出版社，2004 Feng Q L.The control theory[M].Beijing:Beijing University of Aeronautics and Astronautics Press，2004

The M om ent Rebalance Controlling Loop Design of HRG

CHEN Xiaojuan，LIKai，WANG Dezhao，LIDong
(Beijing Institute Control of Engineering，Beijing 100190)

Basic constitute and control principle of HRG is presented in this paper.The design of frequency-domain characteristic of the moment rebalance control loop as the core control loop is described，and its implementation is given.Verification test indicates that the design is correct and available.

HRG;moment rebalance control loop;characteristic in frequency-domain

V241.5

A

1674-1579(2012)03-0033-04

10.3969/j.issn.1674-1579.2012.03.007

陈小娟(1970—)，女，高级工程师，研究方向为航天惯性敏感器;李 恺(1979—)，男，工程师，研究方向为航天惯性敏感器;王德钊(1939—)，男，研究员，研究方向为航天陀螺电路;李 东(1949—)，女，研究员，研究方向为航天陀螺电路.

2011-05-16