基于星敏感器的卫星角速度估计精度分析

李 晓，赵 宏，武延鹏，王 立

(1.北京控制工程研究所，北京100190;2.中国空间技术研究院，北京100094)

基于星敏感器的卫星角速度估计精度分析

李 晓1，赵 宏2，武延鹏1，王 立1

(1.北京控制工程研究所，北京100190;2.中国空间技术研究院，北京100094)

重点研究星敏感器自身特性对角速度估计精度的影响，分析了星敏感器动态情况下恒星矢量测量精度，推导出恒星矢量测量误差与星像目标中心提取误差之间的关系;进而研究了最小二乘角速度估计算法的精度，得出其精度影响因素:星像目标中心提取误差、曝光时间、恒星矢量数目及相互夹角;最后以给定的星敏感器参数和实际恒星分布进行数学仿真，验证了采用星敏感器估计角速度的可行性.

星敏感器;最小二乘;角速度估计

基于星敏感器的卫星姿态角速度确定系统可用于陀螺的故障诊断，同时作为备份，在陀螺失效时为控制系统提供角速度信息.从未来发展趋势看，基于星敏感器的卫星姿态角速度确定可以使姿控系统实现无陀螺化，大大降低姿控系统的重量、能耗、复杂度，提高其可靠性，对实现卫星的小型化，轻便化，廉价化具有重要意义.

目前国内对于这方面的研究主要限于角速度轨迹算法层面，尚无关于星敏感器自身特性对角速度估计精度影响的研究，且算法多基于星图识别，对星图不能识别只利用恒星矢量情况下的角速度估计研究则相对较少.本文结合星敏感器在动态条件下的工作特性，分析了无需星图识别的最小二乘角速度估计算法的精度，并进行了仿真验证.

1 动态条件下星敏感器矢量测量精度

在动态情况下，曝光期间星像在像平面不断移动，星图处理的目的是确定曝光中心时刻恒星矢量在本体系中的坐标，因此采用亚像元细分算法计算的期望值是曝光中心时刻星像中心所处的位置，将其定义为星像目标中心.

1.1 星像目标中心质心法提取误差

通常采用一定窗口区域的像元灰度进行质心法计算，获得星像目标中心，计算方法如下:

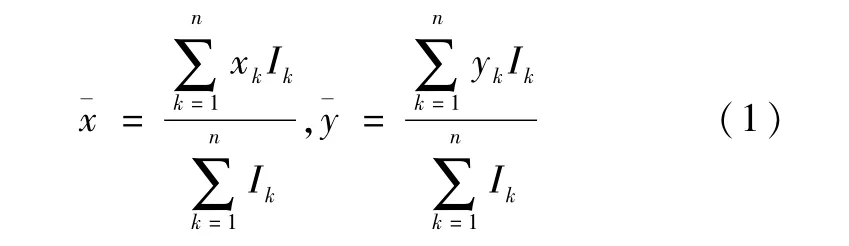
其中xk，yk为窗口区域内第k像元的几何中心坐标，Ik为第k像元的灰度值.

星像目标中心提取误差从性质上可分为两类:一类是算法自身固有的缺陷，一类是由星敏感器像元噪声引起的随机误差.前者相对于后者而言可以忽略，因此本文主要分析由像元噪声带来的随机误差.星敏感器像元输出灰度满足正态分布，其均值I和标准差σI为[1]:

其中μs为有效信号电荷的均值，μdark为暗电流均值，μB为背景均值，σron为读出噪声，σquan为量化噪声，m为电荷与灰度之间的比例系数.

各像元的随机误差是不相关的，根据随机误差的传递公式可得¯x的方差:

令

则:

可以看出αx、βx反映了窗口区域的形状、大小、信号电荷分布对随机误差的影响，而与 μ0、μdark、μB、σron、σquan无关，可由星像能量分布函数通过数值计算获得αx、βx的值，从而定量得出星像目标中心的质心法提取误差[1].

1.2 恒星矢量测量精度

经过校准后的星敏感器恒星矢量的测量误差主要来自于星像目标中心提取误差.设星敏感器视场内某恒星的星像目标中心在像平面的理论坐标为[x y]，设l=[-x-y f]T，f为焦距，将其单位化，得到恒星矢量的理论值为 ls=设l的量测值为lm=l+Δl，其中为星像目标中心提取误差，nz为焦距误差.将lm单位化，得到该恒星矢量的测量值lms=ls+Δls，Δls为矢量测量误差，可由一阶近似获得[2]:

设ν为恒星单位矢量在本体系的坐标，M为安装矩阵，ν=M ls，则本体系恒星矢量测量误差为:

nz的标准差σz=0，为简化分析，令σx=σy=σz= σ¯xm，且nx、ny、nz相互独立，其中σ¯xm为误差上限，则Δν的协方差阵为:

用f2近似代替可得:

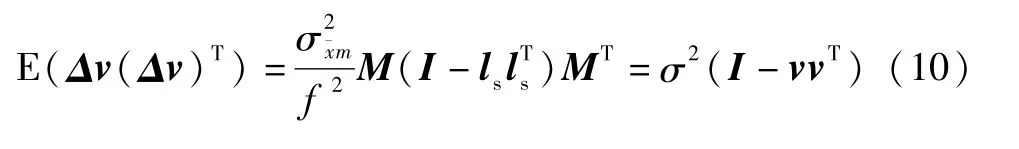
2 最小二乘角速度估计精度分析

恒星矢量在本体系中的基本运动方程为:

式中[v(t)×]为反对称阵.假设T时间内角速度为定值，设v(k)为初始矢量，v(k+T)为末矢量，令:

式(11)可近似为:

若获得n(n≥2)个恒星矢量，可得:

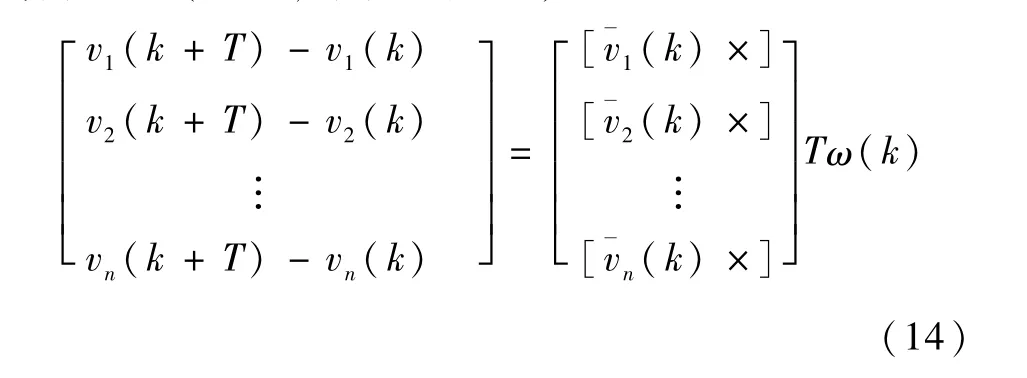
由此可得角速度的最小二乘解为:

2.2 精度分析

设恒星i在本体系的初始单位向量为νi1，经过时间T后变为νi2，其量测值分别为~νi1，~νi2:

设不同矢量的测量误差互相独立，由式(10)得:

在体育馆操场练习“蹲”，刚开始感觉挺别扭，还不好意思，但在好心阿姨、叔叔的指导下，我慢慢进入了状态。经过几天练习，我感觉轻松多了。有时练习，来一小段音乐，整个人便进入了放松状态，呼吸也慢慢合上了音乐的节拍，“蹲”起来更加轻松自如，当然，也促进了血液循环，缓和了紧张的神经和肌肉，安神定志。

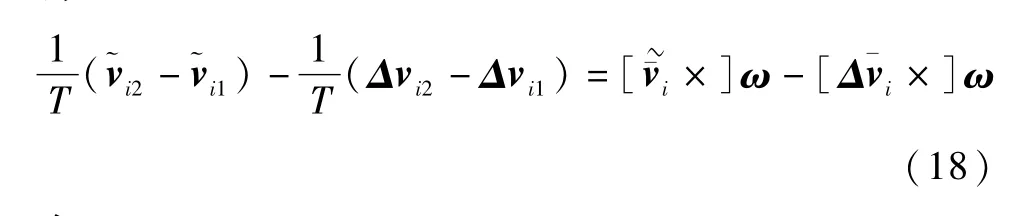
令

则

若T≤0.5s，ω≤2(°)/s，则 [ω×]≪1/T，因此:

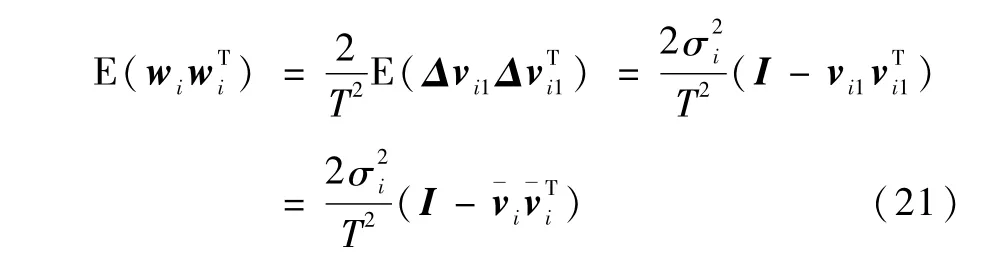
采用n颗星最小二乘算法可得到角速度估计值为:

由式(18)和(19)可得:

将式(23)代入式(22)得角速度估计误差为:

设σ1=σ2=...=σn=σ，令忽略与的差别，只考虑wi自身对Δω协方差阵的影响[3]，可以得到Δω的协方差阵:

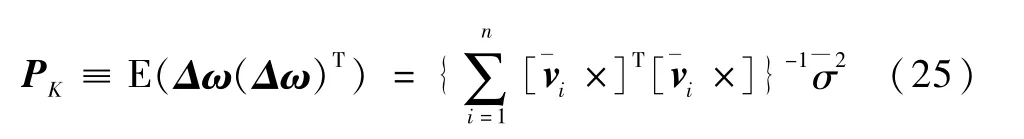
为了直观的比较角速度估计精度的大小，采用ξ=E((Δω)TΔω)=tr PK来衡量估计精度，令A=设λ1，λ2，λ3为B的特征值，由于可得B=n I3×3-A，则n-λ1，n-λ2，n-λ3为A的特征值.因为PK=A-1-σ2，所以

3 给定星敏感器的角速度估计精度分析与仿真

速度估计精度分析.通常卫星会安装2～3个星敏感器，因此可以综合利用多个星敏感器的恒星矢量测量信息进行角速度估计，从而提高精度和成功率.

表1 给定星敏感器的参数Tab.1 Parameters of the given star sensor

经分析，选择光轴相互垂直的三个星敏感器用于角速度估计效果最好.采样时间T选择为0.5s，曝光时间选择为最优曝光时间[1]，并适当调整使其与采样时间满足倍数关系.根据动态情况下星敏感器的探测灵敏度可计算出星敏感器探测到的极限星等[4]，为减小系统的计算量，星等大于4.5的恒星矢量予以舍弃，根据角速度估计采用的最暗的星计算矢量测量误差上限σmax，利用蒙特卡罗法随机产生恒星矢量，计算γ值，重复10000次，计算平均值γmean，最终得出角速度估计相对精度ERmax，由此估算出当前配置下星敏感器的角速度估计能力如表2.

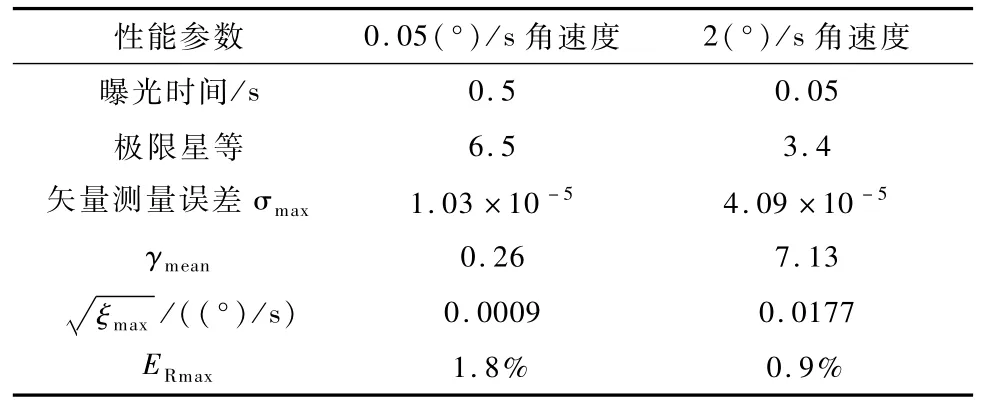
表2 给定星敏感器的角速度估计精度分析Tab.2 Accuracy analysis of the angular rate estimation for the given star sensor

卫星的运动采用卫星动力学模型进行仿真，角速度的初值分别取[0 0.05 0]T(°)/s和[0 2 0]T(°)/s，卫星姿态和角速度在无控状态下自由变化，为保证一定的天球覆盖率，每5s变换随机变换一次姿态，改变星敏感器的指向天区，姿态变换时保持角速度不变，仿真结果见图1和图2.

图1 角速度为0.05(°)/s时的仿真结果Fig.1 Simulation resultwhen angular rate is 0.05(°)/s

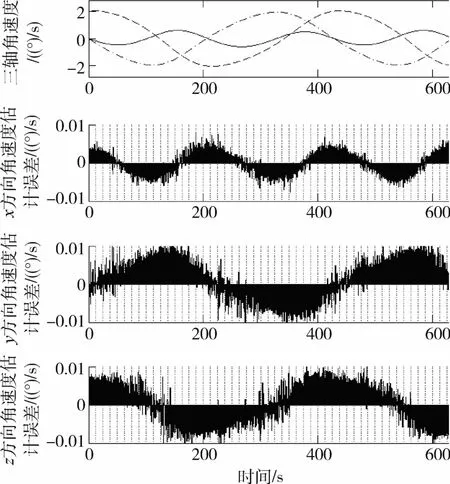
图2 角速度为2(°)/s时的仿真结果Fig.2 Simulation result when angular rate is 2(°)/s

对由最小二乘法得到的角速度估计误差进行统计，得到ER的值分别为1.6%和0.4%.可以看出，角速度估计精度在理论计算范围内，相对精度优于2%.由于角速度是时变量，最小二乘角速度估计方法具有一定的滞后性，因此当角速度呈递减趋势时，角速度估计存在正向偏差，反之当角速度呈递增趋势时，角速度估计存在负向偏差.

4 结 论

本文首先分析了动态情况下星像目标中心提取误差和恒星矢量误差的定量估计方法，重点从理论上分析了最小二乘算法的精度，在分析过程中采用误差放大的方法，获得角速度估计误差可能出现的最大值，并对给定的星敏感器的角速度估计能力进行分析和仿真，仿真结果与理论分析结果一致.

最小二乘角速度估计是角速度估计方法中最简单的一种，只利用恒星矢量在卫星本体系中的变化量，不需要进行星图识别，计算简单.通过对星敏感器的各种参数进行合理配置，可以使最小二乘角速度估计精度达到较高的水平.当角速度是时变量时，最小二乘角速度估计具有一定的滞后性，存在理论上的系统偏差，若采取相应的滤波措施，可进一步提高精度.

[1] 李晓，赵宏.卫星转动条件下APS星敏感器星像目标中心提取精度分析[J].空间控制技术与应用，2009，35(4):11-16 Li X，Zhao H.Analysis of star image centroid accuracy of an APS star sensor in rotation[J].Aerospace Control and Application，2009，35(4):11-16

[2] 刘一武，陈义庆.星敏感器测量模型研究[C].全国第十届空间及运动体控制技术学术年会论文，北京，2002 Liu Y W，Chen Y Q.Study on star-sensormeasurement model[C].The 10thSpacecraft Control Technology Conference，Beijing，2002

[3] John L C.Angular velocity determination directly from star tracker measurements[J].Journal of Guidance，Control and Dynamics，2002，25(6):1165-1168

[4] 李晓，赵宏，卢欣.动态情况下星敏感器探测灵敏度研究[J].空间控制技术与应用，2010，36(1):37-41 Li X，Zhao H，Lu X.Study on detection sensitivity of star sensor in dynamic state[J].Aerospace Control and Application，2010，36[1]:37-41

Analysis on Accuracy of the Satellite Angular Rate Estimation Based on Star Sensor

LIXiao1，ZHAO Hong2，WU Yanpeng1，WANG Li1
(1.Beijing Institute of Control Engineering，Beijing 100190，China; 2.China Academy of Space Technology，Beijing 100194，China)

The influence of star senor's characteristics on the accuracy of satellite angular rate estimation is emphatically studied.The relation between errors of star image centre extraction and accuracy of star vectormeasurement is analyzed.The accuracy of the least-square angular rate estimation is deduced，and then factors influence of error of star image centre extraction，the exposure time，the number of star vectors and theirmutual angles on estimation accuracy.A simulation is set based on the given APS parameter and actual star distribution.

star sensor;least-squares;angular rate estimation

V249

A

1674-1579(2012)03-0016-05

10.3969/j.issn.1674-1579.2012.03.004

李 晓(1984—)，男，工程师，研究方向为星敏感器;赵 宏(1962—)，男，研究员，研究方向为卫星总体设计;武延鹏(1977—)，男，研究员，研究方向为星敏感器设计;王 立(1977—)，男，高级工程师，研究方向为空间光学敏感器设计.

2011-09-21