考虑高度参数的摆动式红外地球敏感器模型研究

唐 尧

(北京控制工程研究所，北京100190)

考虑高度参数的摆动式红外地球敏感器模型研究

唐 尧

(北京控制工程研究所，北京100190)

本文考察了摆动式红外地球敏感器测量的工作原理，在介绍敏感器两种数学模型—圆盘模型和三维模型的基础上，增加卫星轨道高度参数为变量，讨论了在不同轨道高度下，敏感器数学模型的变化.利用小角度条件下的一阶近似处理，对敏感器模型所关心的弦宽与姿态角转换关系给出了解答.通过进行带有高度参数的修正，把敏感器的圆盘模型和三维模型推广到了其他轨道高度下.

地球敏感器;轨道高度;摆动扫描式;模型研究

摆动式红外地球敏感器在三轴稳定的卫星上有着广泛的应用.地球敏感器用于测量卫星的滚动角和俯仰角.现有的地球静止轨道卫星上通常只在入轨后的正常工作阶段使用地球敏感器，因此以往的关于摆动式地球敏感器模型的讨论集中在同步轨道高度上，对其他轨道高度的情况鲜有提及.

本文结合摆动式红外地球敏感器的两种数学模型——圆盘模型和三维模型，对不同轨道高度下地球敏感器探头输出与卫星姿态角的转换关系作出讨论，并进行数学仿真.文中提及的敏感器如不特别说明，均指单地平摆动式红外地球敏感器.

1 单地平摆动式地球敏感器工作原理

敏感器对地球的14～16.25μ波段的入射能量进行调制[1].其光学系统包括4束铅笔型射束组成的复合视场，对应四个热敏电阻红外探测器，这四个探测器装在入射物镜的焦平面上，如图 1所示.其中，反射镜的扫描轴与俯仰轴平行，扫描轴由电机驱动转动使得复合视场以一定频率沿俯仰轴扫描.

当卫星处于零姿态时，四个基本视场从同步高度分别沿南北纬45°扫描地球边缘，扫描零点刚好处于地球边缘上.如果卫星姿态发生滚动和俯仰，敏感器探头测量视场扫描到地球边缘时的位置相对视场零点位置所转过的角度即弦宽[2].四个红外探头分别输出四个弦宽值.

图1 摆动式地球敏感器扫描原理图Fig.1 Swing-scanning sketch of infrared earth sensor

2 地球敏感器的圆盘模型和三维模型

地球敏感器数学模型所关心的问题是弦宽与姿态角之间的转换关系.最常见的模型为圆盘模型，另外还有一种更为精确的在三维空间中考察扫描过程的模型称之为三维模型，下面分别介绍.

首先定义如下几个坐标系:

星体坐标系(XbYbZb):星体坐标系是一个正交坐标系，原点在卫星质心，三个坐标轴和星体主惯量轴一致，Xb、Yb、Zb分别称为星体的滚动、俯仰和偏航轴.

地球敏感器本体坐标系(XhYhZh):原点在四个探头基本视场的交点上，三个坐标轴与星体坐标系的三轴一致.

轨道坐标系(XoYoZo):原点在卫星的质心Ob，由质心指向地心的坐标轴是Zo轴;Xo轴在轨道平面上与Zo轴垂直.指向卫星速度方向;Yo轴与Xo、Zo轴组成右手正交坐标系与轨道平面的法线平行.零姿态时，星体坐标系和轨道坐标系重合.

敏感器的四个探头以Zh为对称轴放置，从-Zh轴向+Zh轴看，探头位置如图2所示.

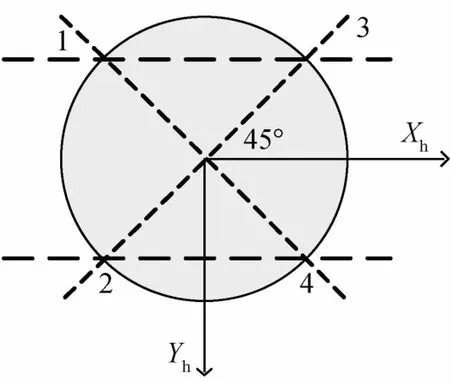
图2 探头安装位置Fig.2 Installation of infrared sensors

在敏感器本体坐标系中，探头扫描视场方向向量分别为

其中α=6.16°，β=6.20°.

2.1 圆盘模型

对敏感器复合视场来说，地球可以看成是基准平面XhYh上的圆盘，扫描过程可以简化为探头对圆盘的扫描.圆盘上的长度量以角度为单位表示.圆盘直径R=ρs=arcsin[-R/(R′+H)];其中，ρs为地球半张角，R′为地球半径，H为卫星轨道高度.考虑地球周边二氧化碳层-R=6378+22=6400km.

当卫星发生滚动和俯仰时，Zh轴偏离地心，地球圆盘中心在坐标平面 XhYh内移到 O′点，如图 3所示.坐标是(-θ，φ)，偏离的距离θ，φ就是卫星的俯仰角和滚动角[3].

图3 圆盘模型扫描图Fig.3 Scanning sketch of disk model

这时，探测器视场的光轴在1′，2′，3′，4′点穿越地球边缘，在敏感器本体坐标系中，这些穿越点所在的圆方程为

令，e=6.17°，e为扫描视场在圆盘中的纵坐标.这些穿越点的横坐标分别为

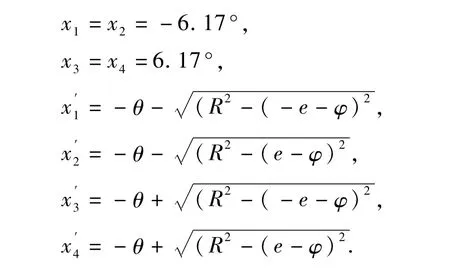
所以敏感器测量得到的弦宽值为

将这些弦宽值组合起来，可以得到敏感器探头输出与姿态角的转换关系:

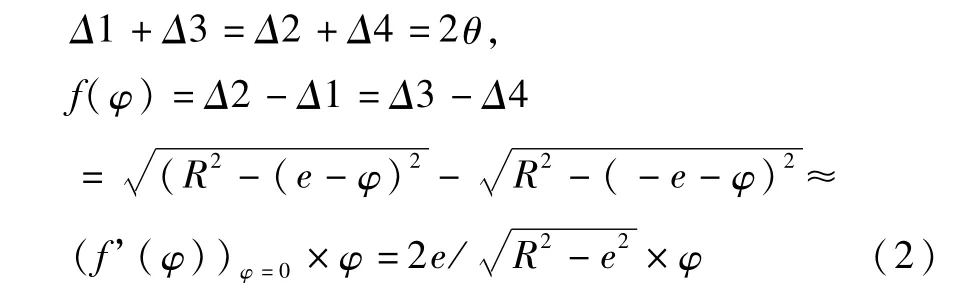
其中，e为固定值，R与卫星高度H相关.在同步轨道高度下，公式满足:

2.2 三维模型

从圆盘模型的推导中，知道圆盘模型把以角度为单位表示长度关系，这在小角度下才能成立.因此，圆盘模型需要满足姿态角和扫描角均是小角度的前提.敏感器实际的扫描过程也不是对平面上圆盘的扫描，而是在三维空间中对地球边缘的扫描.

三维空间的探头扫描如图 4所示.以探头3为例，rh为扫描视场的零点位置，re为扫描视场扫描到地球边缘时的位置.

图4 三维模型探头扫描示意图Fig.4 Scanning sketch of 3-D model

在卫星控制系统的动力学模型中，对卫星姿态的计算都是用方向余弦阵或者姿态四元数进行的.所以在三维模型中，从卫星姿态的方向余弦阵出发，推导探头输出的弦宽[4].令卫星方向余弦阵为

可以得到:

令面YhOZo与面YhOZh的夹角为δ.在轴Zh轴Zo轴Yh组成的球面三角中，应用球面三角函数，得到:

即:

不妨设地心矢量在-X轴一侧.令k为面reOYh与面YhOZo形成的二面角.在轴re轴rh轴Zo组成的球面三角形中，应用球面三角函数，得:

其中，因为扫描视场与敏感器本体Yh轴夹角不变，对探头1和3，∠reOYh=α+90°=96.17°.对探头2和4，∠reOYh=90°-α=83.84°.ρs=arcsin[-R/ (R+H)].令另外，根据探头安装位置，rhOYh已知面YhOZh与面的夹角β=6.20°.

综合，式(3)和式(4)，可以得到各个探头输出的弦宽即面reOYh与面rhOYh的夹角为:

从以上的推导过程中，可以看出三维模型给出了卫星姿态与真实弦宽的精确对应关系.因此，认为三维模型中计算得出的弦宽就是理论上地敏探头的真实输出.但同时，也发现从弦宽精确计算卫星姿态将是一个复杂的过程，所以希望得出一个类似式(2)的从弦宽到姿态角的简单转换关系.

这里，需要用到小角度近似.在小角度下，∠YhOZo≈90°-φ，δ≈θ.所以，得到:

弦宽为:

把k1，k2在φ=0附近展开，得到:

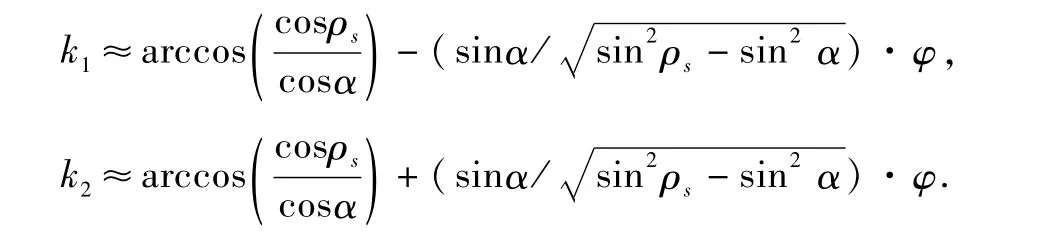
把各个探头的弦宽值组合起来，可以得到探头测量弦宽与姿态角的转换关系:

其中，α是探头安装位置决定的固定值;ρs为地球的半张角，与卫星高度有关.在同步轨道高度下，公式满足:

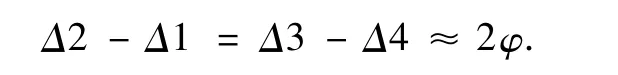
从以上的两种模型的推导结果可以看出，在不同的卫星高度下，姿态角与弦宽的转换公式不一样.而关于卫星姿态姿态轨道控制的一些经典著作如文献[1]，文献[3]以及另外有关摆动式红外地球敏感器的文章中所提及的数学模型都只讨论同步轨道高度下的情况，所应用到的转换关系也仅是:

这就导致了关于敏感器模型的一种误解，即在非同步轨道高度下仍然沿用式(6)所表示的转换关系.

下面对上述推导结果进行仿真分析和验证.

2.3 数学仿真分析及验证

把滚动角和俯仰角固定为一组典型值，取φ= 1°，θ=4°，转动顺序为Z轴-X轴-Y轴.

在窄扫模式下，探头输出的弦宽值区间为-5.5°到+5.5°，超出这个范围探头扫描不到地球边缘，探头输出会被屏蔽掉(计算中取0处理).各探头输出弦宽如所图5图6示.

从图5和图6的计算结果，看出圆盘模型和三维模型得出的弦宽值几乎一样，这说明在小角度情况下，两种模型对弦宽的计算是统一的.

敏感器要输出有效的滚动角和俯仰角，至少需要三个探头的弦宽值.在敏感器有效的范围内，圆盘模型和三维模型按照式(6)计算的姿态角误差，如图7图8所示.

图5 圆盘模型下各探头输出弦宽Fig.5 Output chord length of disk model

图6 三维模型下各探头输出弦宽Fig.6 Output chord length of 3-D model

图7 三维模型姿态角误差Fig.7 Euler angle error of 3-D model

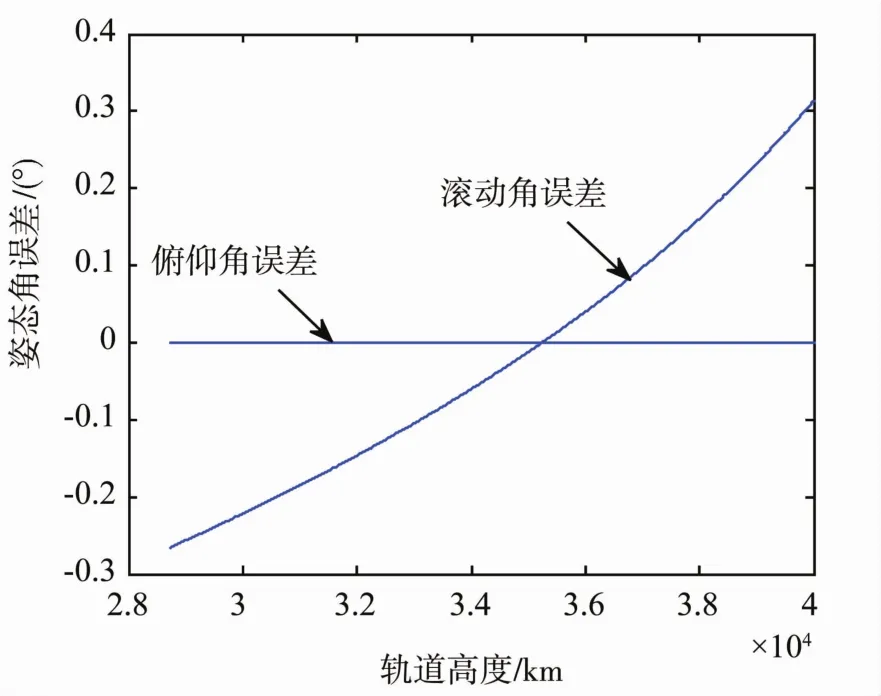
图8 圆盘模型姿态角误差Fig.8 Euler angle error of disk model

从图7和图 8的仿真结果可以看出，俯仰角误差保持为0，这是因为扫描轴与俯仰轴平行，俯仰角的计算与轨道高度无关，弦宽与俯仰角具有直接线性相关.滚动角误差在高度为 29000km时，达到25%左右.在高度为40000km时，达到30%左右.在同步轨道高度附近，接近于0.这说明公式(6)只在同步轨道高度附近成立.

两种模型分别按照式(2)和式(5)进行修正，得到结果如所示.

从图9和图10可以看出，通过式(2)和式(5)修正后，在仿真范围内，滚动角的最大误差在6%以内.模型存在误差的原因是由于式(2)和式(5)均是对弦宽差值函数的一阶近似.另外，也发现随着轨道高度的减小，滚动角误差值也在减小，这说明在低轨道高度下，式(2)和式(5)的计算结果与实际值更为相符.

图9 圆盘模型修正后的姿态角误差Fig.9 Euler angle error of calibrated disk model

图10 三维模型修正后的姿态角误差Fig.10 Euler angle error of calibrated 3-D model

既然式(2)和式(5)会引入一定的滚动角误差，还需要考察该误差对卫星姿态控制的影响.取轨道高度为30000km，俯仰角固定为0°，滚动角在-3.5°至3.5°范围内变化.随着卫星姿态变化，计算误差如图11所示.

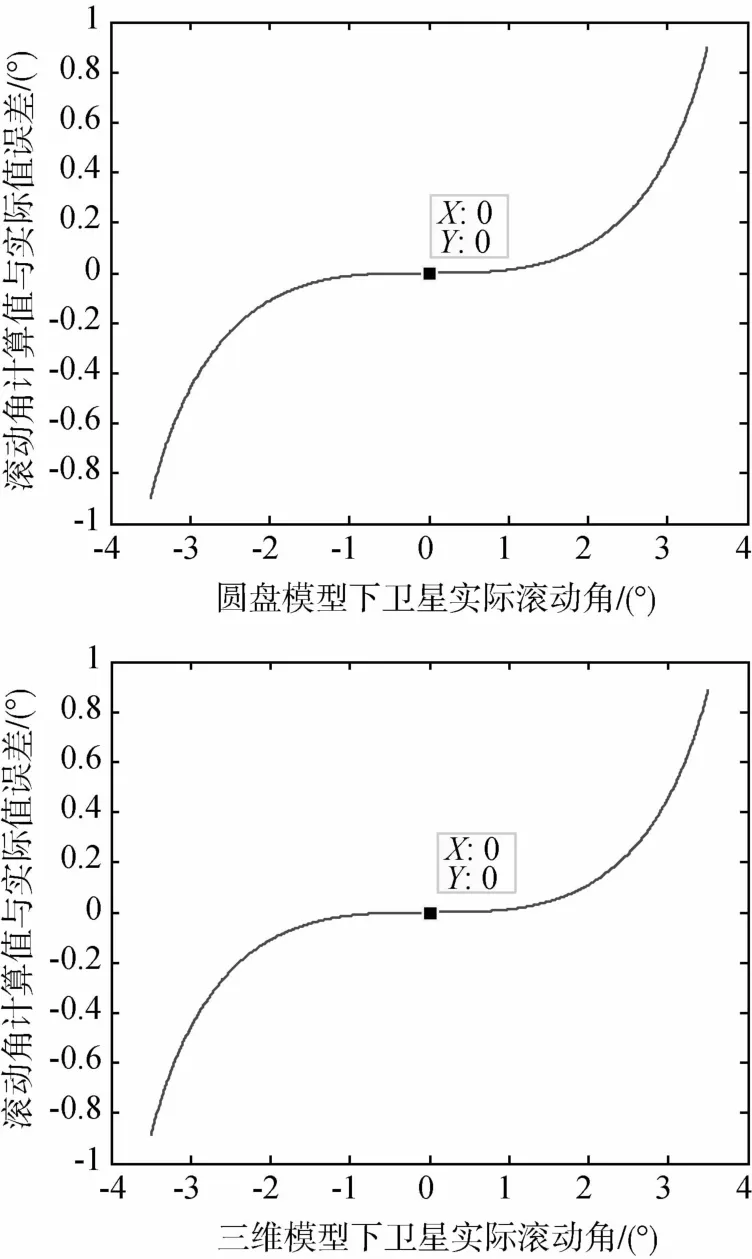
图11 模型计算出的滚动角与真实滚动角的比较Fig.11 Roll angle error between theoritical value and measured value

从图 11中，可以看出模型引入的滚动角误差随着卫星趋于零姿态而收敛于零.滚动角的计算值与真实值单调正相关，并且同号.这说明当按照姿态角计算值对卫星实施控制可以使卫星的姿态最终收敛于零姿态，即卫星是可控的.

3 结 论

通过数学仿真，得出如下结论:

本文给出了考虑轨道高度的摆动式红外地敏的两种模型:圆盘模型和三维模型.三维模型以地敏测量坐标系相对于轨道坐标系方向余弦阵为输入，给出了地敏四个探头输出量，揭示了地敏测量的本质;圆盘模型以滚动、俯仰角为输入，利用平面几何计算，在小角度下是可以应用的.从计算结果看，利用三维模型进行姿态解算，在近似简化算法，高度对于俯仰角没有影响，对于滚动角有一定影响，滚动角越大，误差越大.在滚动角是0时，误差是0.

[1] 吕振铎.卫星姿态测量与确定[M].北京:中国空间技术研究院. Lv Z D.Measurement and determination of spacecraft attitude[M].Beijing:China Academe of Space Technology.

[2] 张国玉，姜会林，徐熙平，等.红外地球敏感器扫描镜摆角激光动态测试方法[J].光学学报，2007，27(5): 875-881. Zhang G Y，Jiang H L，Xu X P，et al.Laser dynamic tesing method for swing angle of scaning mirror of infrared earth sensor[J].Acta Optica Sinica.2007，27(5): 875-881

[3] 章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社，1998 Zhang R W.Dynamics and control of spacecraft orbit and attitude[M].Beijing:Beijing University of Aeronautics and Astronautics Press，1998

[4] 刘新彦.利用摆动地球敏感器两个探测器输出的姿态确定[J].空间控制技术与应用，2008，34(2):14-17. LIU X Y.Spacecraft attitude determination using two detector of swing earth sensor[J].Aerospace Control and Application，2008，34(2):14-17

Research on Sw ing Scanning Infrared Earth Sensor w ith O rbit A ltitude Concerned

TANG Yao
(Beijing Institute of Control Engineering，Beijing 100190，China)

The model of swing-scanning infrared earth sensor(SSIRES)at different orbit altitudes is researched in this paper.By reviewing the swing-scanning Process of infrared earth sensor(IRES)，two models，as disk model and 3D model are introduced by taking orbit altitude as a variable.The transformation from the earth chord length to attitude angles is established approximately in the condition of spacecraft closing to zero position，so that the models are extended to all kinds of orbits through calibration for interested orbit altitudes.

infrared earth sensor;orbit altitude;swing-scanning;model research

TN379

A

1674-1579(2012)03-0027-06

10.3969/j.issn.1674-1579.2012.03.006

唐 尧(1987—)，男，硕士研究生，研究方向为航天器地面测试与故障注入.

2011-12-23