光学薄膜椭圆偏振数据反演的优化算法

童晟飞，王正忆，陈 星

（浙江大学 理学部 物理系，浙江 杭州310027）

1 引 言

材料薄膜的厚度、光学常量是膜系设计、材料研究和薄膜制备中不可缺少的参量．膜厚和光学常量不能由椭圆偏振仪直接给出，后期需要经过一系列的拟合计算．椭圆偏振法由于无须测定光强的绝对值，因而具有很高的精度和灵敏度．对超薄膜（可达1 nm以下）同样具有很高的灵敏度．如果椭圆偏振仪的起偏器和检偏器回转角有0．01°的精度时，则膜厚0．007 nm的变化就可能被检测出来．由于椭偏参量确立的方程是超越方程，无法直接从测量数据通过计算得到薄膜参量的解析解［1］，需要进行反演计算，可通过优化算法做数值反演解．本软件运用C＋＋语言通过变步长迭代循环的优化算法开发数据处理程序，能够直接根据输入的数据得到结果，无需进行查表或作图等人工操作，并且适应性较广（可以接受任意的激光波长和基底材料），速度较快（平均运行时间2 s），精度较高（折射率精确到0．001，厚度精确到0．01 nm）．程序可以接受1组测量数据或者激光入射角不同的2组测量数据，输入1组数据时程序会输出所有符合方程的解（包括跨周期的解），要得到唯一的解，需要改变椭偏仪的入射光角度后再进行1次实验，2种情况下重叠的解即为最终结果．对于有吸收的薄膜，即折射率为复数，用了结合模拟退火法的量子行为粒子群混合算法进行计算，QPSO算法包含比较当前粒子的适应值与其历史最优值以不断刷新历史最优值的过程迭代更新，系统就能够获得摆脱局部能量极小点的机会，并找到一个更好的、更接近于整体的极小点［2］．

2 基本原理

若有一偏振光在样品表面反射，如图1，可以将其分解成为在2个互相垂直方向上的分量波：振动面平行入射面的线偏振光称p波，振动面垂直入射面的线偏振光称s波．

图1 光波在单层薄膜中的传播

在界面1和界面2菲涅耳反射系数分别为［3－5］：

其中，n0为空气折射率（n0＝1．0），n为膜折射率，ns为衬底折射率（可以是复数折射率），θ0为入射角，r1p和r1s是界面1上p光和s光的反射系数，r2p和r2s是界面2上p光和s光的反射系数．薄膜的反射率可由菲涅耳反射系数表示为

其中，

为使计算方便，定义ψ和Δ使之满足下列关系［2］：

所以理论上只要确定ψ和Δ后，就可解出n和d．

3 薄膜无吸收情况的处理

当薄膜无吸收时，比较简单的求解程思路是：将n从0．01到5．00，d从1 nm到500 nm的数值逐一代入方程，求出相应的ψ和Δ，然后与输入值进行比对，当误差精度小于指定的范围时，就将这一组n和d输出．程序使用的是固定步长，利用固定步长计算将会导致程序运行时间过长，计算量浪费．

作出（ψi，Δi）关于（n，d）变化的图，找到图上表现为尖锐的峰，说明（ψi，Δi）随（n，d）的变化较快．可见，对于绝大多数n和d，对应的ψ和Δ都与输入值相去甚远，只有在接近方程组的解时，ψ和Δ才会接近输入值［4］．

所以本程序使用可变步长来进行n和d的循环．根据对大量实际计算的总结，发现n的改变对ψ和Δ的影响很大，而d的改变产生的影响相对较小，因此对d使用可变步长．

3．1 第1步循环

具体方法是：n从0．01到5．00以步长0．01循环，d从1到501以5为步长进行循环，当｜δψ｜＜1且｜δΔ｜＜3时，以1为步长对d－4到d＋4范围内的d进行逐一计算．计算完成后恢复5为步长．

建立存放10组解的数组，存放n和d，把n，d代入方程作正解．计算出的ψ和Δ的误差精度ε＝｜δψ｜2＋｜δΔ｜2．每计算1组n和d，将ε与数组中10组解对应项分别进行比较．如果计算得到的解的偏差小于已存放的偏差最大的解，则替换偏差最大的这组解．这样，在完成循环时，存放在数组中的解就是δψ与δΔ相对最小的解，即误差精度ε为最小．

程序算法的流程图如图2所示．

图2 第1步循环

3．2 第2步循环

在进行第1次循环之后，得到了10组近似的解．这些解的精度还是不够的，需要进行更精确的计算．实际上，第1次循环得到的10组解并不是孤立的，这些解的折射率n值通常都集中在1个数值附近．通过编写1个函数可以将这些解归纳起来，得到1组近似解，并使这组解中的厚度d为相近的n值对应的所有d值中最小的．

对这组解分别再进行1次循环，其中n的循环从n－0．05开始，到n＋0．05终止，步长为0．001；对应的d的循环从d－2到d＋2，步长为0．01．建立1个数组，只存放1组解，对解的筛选方法和前面相似，只是这次只保留偏差最小的解．这样的循环可以使n精确到小数点后3位，d精确到小数点后2位，从而达到精确度的要求．

程序算法的程序图如图3所示．

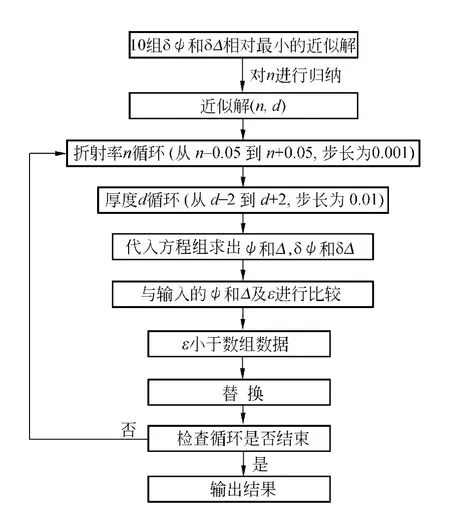
图3 第2步循环

3．3 厚度周期的计算

厚度d具有周期性，这是由（5）～（7）式中的e指数决定的．e－2iδ这一项的δ以π为周期，所以d的周期为

3．4 最终结果

第2次循环得到的2组解分别加上整数个周期即为方程最终的解．

从上面的分析可以看到，仅通过1组实验数据得到的解是不唯一的，要得到唯一的解，需要改变椭偏仪的入射光角度后再进行1次实验，2种情况下重叠的解即为最终结果．

要测量膜厚过1个周期的真实厚度，可采用改变入射角的方法．从表1可以看出：样品3和5薄膜在2个不同的入射角测量下，2组测量厚度基本相等，薄膜的厚度相差0．580 nm，0．260 nm，相应的周期厚度相差4．750 nm，1．180 nm，薄膜的真实厚度应该在1个周期厚度以内．从表1看出4号样品薄膜在2个不同的入射角测量下厚度相差7．19 nm，相应的周期厚度相差6．69 nm．因为膜的厚度是唯一的，所以一定叠加周期厚度．对于重合解的判断，需要控制好精度．如果精度过高可能会找不到重合解，而精度过低则容易导致周期判断错误．一般地，2次入射角相差越大则厚度周期相差得也越大，此时可以降低重合的精度；而入射角相差较小时厚度周期也相差得比较小，此时就必须使用较高的重合精度．

本程序设置了相应的参量．在本程序中，利用2组数据分别得到的折射率n相差不能超过入射角之差（使用角度作为单位时的数值）的0．001倍（最小不低于0．005），否则视为误差过大．对于2组数据的每个厚度周期，判断厚度d相差是否超过入射角之差的0．1倍（最小不低于0．5 nm），如果超过，则认为薄膜不是位于这一周期，继续搜索其他的周期厚度，直到找到重合的为止．

表1 薄膜样品的计算结果比较数据

3．5 计算结果的检验

用上述算法开发的软件对在单晶硅衬底上经过热氧化形成的SiO2／Si薄膜样品1和2进行分析［3－4，6］，对不同的数据处理方法进行比较．选定相关参量衬底如下：样品1，2，4单晶硅衬底（n＝3．85－0．02i）． 样 品 1 和 2 入 射 光 波 波 长635 nm．样品4入射光波波长为632．8 nm．样品3和5为K9玻璃（n＝1．515）上的TiO2薄膜．入射光波波长为632．8 nm．要测量膜厚过1个周期的真实厚度，可采用改变入射角的方法．样品采用上述两步迭代循环逼近计算，可得材料折射率n和厚度d的值．样品4的最后结果界面如图4所示，整个计算过程大约持续了2 s．表1为本软件与国外仪器软件及国内其他软件［4，6－8］的比较．本文算法计算的折射率和厚度已分别精确到第3位和第2位的稳定解，表明只要实验测得的（ψ，Δ）足够精确，就能够得到足够精确的（n，d）．

图4 样品4的最后结果界面

因为镀完膜的样品折射率和厚度在理论上是唯一的，所以选择2个相差不大的入射角分别计算应该得到同样的折射率和厚度结果，由此可以从多周期的解中确定出薄膜的真实折射率和厚度，以及样品是否跨周期的判断．

4 薄膜有吸收情况的处理

对光有吸收的薄膜，除了折射率n和厚度d之外，还存在消光系数k，一共有3个未知数要求解．如果通过一定的实验方法能够确定这3个未知数中的1个，则可以通过前面的变步长循环迭代的算法进行求解．

如果3个未知数都不能预先确定，对于前面的变步长循环法，虽然已经有所优化，但用于处理这种情况仍然不适应，为此需要使用更加优化的算法．常见的优化算法有遗传算法、粒子群算法、模拟退火算法等．

4．1 粒子群算法

粒子群优化（particle swarm optimization）算法是广泛应用的优化算法，基本思想是，将每组（n，k，d）视为三维空间中的1个点，然后一群粒子随机地在该空间中运动，各粒子之间独立运动的同时保持着一定的联系．当1个粒子接近方程解所对应的点时，其他的粒子就会向这个粒子的方向靠近，从而使所有粒子达到收敛点．

4．2 量子行为粒子群算法和模拟退火算法

在传统的粒子群算法中，粒子按照轨道运动，而有限的轨道无法覆盖解空间中的每个点．因此传统PSO算法不能保证收敛到全局最优点．同时，如果1个粒子找到了较好的点，其他的粒子也会朝这个方向运动，一旦粒子都到达这个较好的点附近，就可能无法发现其他更好的点，导致早熟收敛．

为了避免上述问题，人们提出了量子行为粒子群优化（quantum behaved particle swarm optimization，QPSO）算法．

在QPSO中，粒子不再有轨道的概念，而是按照量子力学的原理在解空间中运动．在这一模型中，通过适应度函数判断粒子在某个位置的优越程度．每个粒子每次迭代时记录它的历史最优位置pbest，并与其他所有粒子的pbest进行比较得到种群的历史最优位置gbest．设p点为pbest与gbest之间的任意一点，将p点设为一个delta势阱，利用量子力学原理计算粒子出现在某点的概率，通过蒙特卡罗模拟的方式来测量粒子的位置，从而对粒子进行刷新．

刷新粒子的具体方法是［7］：

1）对粒子的每一维，在pid和pgd之间得到1个随机点，

2）计算所有粒子的平均最好位置mbest，

3）计算评价参量

其中1／g也称为创造系数，可以用β表示．4）刷新位置，

U（0，1）属于（0，1）上区间的随机数．

QPSO虽然能够保证算法的全局收敛性，但是在收敛的情况下，由于所有的粒子都向最优解的方向飞去，导致粒子的多样性损失，使得后期收敛速度明显变慢，容易陷入局部最优．

为了解决这个问题，需要考虑与其他优化算法结合使用．模拟退火算法（simulated annealing，SA）是一种全局搜索能力极强的算法．该方法起源于金属冷却退火这一自然现象．从能量的角度分析，对于一个在温度为T的处于热力学平衡的体系，其在某一微观状态内能为E时的概率分布服从玻耳兹曼分布；系统按照概率f分布于所有不同的能量状态中，即使在很低的温度下，系统也可能处于较高的能量状态，因此，相应地系统就能够获得摆脱局部能量极小点的机会，并找到一个更好的、更接近于整体的极小点［1，9］．

将评价函数设置为系统的“能量”，即为模拟退火算法，该方法具有极强的全局搜寻能力，可以有效避免陷入局部最优的问题［8］．

在SA中，从一个状态过渡到另一个状态的概率为

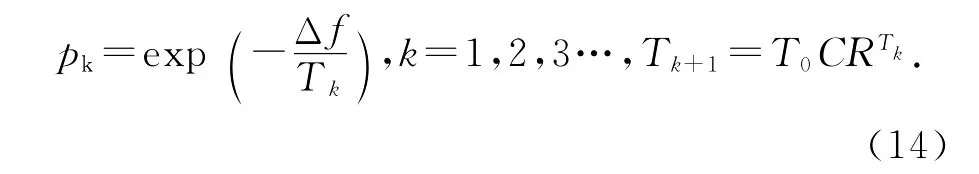
其中－Δf在本问题中为适应度之差．当温度从初始温度逐渐降低到零点时，可以认为系统已经到达最优状态，求解完成．

4．3 结合模拟退火法的量子行为粒子群的混合算法

SA的全局搜索能力很强，但收敛速度偏低．相比之下，QPSO在收敛速度方面更有优势．为了更好利用2种算法各自的优点，可以将SA算法混入QPSO算法中．

QPSO算法包含比较当前粒子的适应值与其历史最优值以不断刷新历史最优值的过程．这个选择过程会指导其他粒子搜索适应值相对好粒子的附近空间，这一过程中低适应值的粒子将被抛弃．然而，那些低适应值的粒子可能具备潜在的更好的进化趋势，这样就降低了整个种群的进化．为了解决这一问题，将模拟退火的概念引入这一过程，低适应值的粒子将以一定概率被接受．这样具有较好进化趋势的低适应值粒子在搜索空间会以一定的概率继续飞行，可以有效地避免陷入局部最小值［7，10］．

由此形成了一种混合算法，流程图如图5所示．在该算法中共有3个参量需要调节：创造系数β，退火初始温度T0，退火常量CR．这些参量决定了整个收敛的准确度以及收敛速度的快慢，需要根据求解的问题来不断尝试．在本问题的求解中，设定β＝1．2，T0＝50，CR＝0．98．

图5 SA－QPSO算法流程图

4．4 计算结果的检验

将一些模拟计算来验证这种算法用于椭偏反演计算的可行性及有效性．在玻璃衬底上的单层TiO2模型及SiO2／Si模型薄面样品进行分析，TiO2模型的参量值为：n＝2．625，k＝0．015，d＝417 nm，ns＝1．523，ks＝ 0，入射激光波长λ＝370 nm，从这些数据可以计算得到（ψ，Δ）在入射角分别为45°，60°，70°，80°时的准确值，具体数据见表2［1，7－9，11－14］．SiO2／Si 模 型 参 量 值 为：n＝1．46，k＝0，d＝108 nm，ns＝3．85，ks＝ －0．02．计算在入射角分别为45°，60°，70°时的准确值，具体数据见表3［15］．

可根据实验数据（ψi，Δi）作出（ψi，Δi）关于（n，d）变化的图，找到图上表现为尖锐的峰，估算k，n，d值的范围．求解时设定消光系数搜索范围为［0，0．2］，折射率范围［0，4］，厚度范围［30，500］．

利用混合算法编写的程序数据进行处理，每次选取2组数据进行计算，得到的结果如表2～3所示．可以看出，程序具有较高的求解精度，求解误差通常能达到10－7的水平，表明对于精确的测量值，程序可以给出比较准确的计算．

表2 TiO2模型3组数据计算结果比较

注：n′，k′，d′为其他软件求解值［7－8，12－13］．

表3 SiO2／Si模型2组数据计算结果比较

从表2～3可以看出：对于有吸收薄膜样品用结合模拟退火法的量子行为粒子群混合算法，其反演得到薄膜光学常数计算结果精确．

5 结 论

本文提出变步长循环的优化算法对没有吸收薄膜样品计算速度快（2 s左右），准确性高（n精确到0．001，d精确到0．01 nm）．程序计算过程中没有使用随机数，因此同一组数据，每次计算的结果都相同．利用2组数据确定了多周期真实厚度．对于有吸收薄膜样品本文提出了利用加入模拟退火的量子行为粒子群优化算法．本程序改善粒子群的全局、局部搜索能力和收敛速度，是具有很强全局搜索能力的算法，可以在保证计算速度的情况下减少早熟收敛的发生．利用量子力学原理计算粒子出现在某一点的概率，通过蒙特卡罗模拟的方式来测量粒子的位置，从而对粒子进行刷新，可很快跳出局部极小收敛达到全局最优点．

［1］ 廖清君．单波长消光椭偏仪的数据处理研究［D］．成都：四川大学，2002．

［2］ 刘细成．透射光谱法测量薄膜参数的研究［D］．成都：四川大学，2003．

［3］ 张丽娟．透射光谱法测量光栅参数的研究与全抗反射膜的设计［D］．成都：四川大学，2005．

［4］ 陈星，童晟飞，王正忆，等．椭圆偏振仪测量薄膜折射率及周期厚度解的分析［J］．实验技术与管理，2011，28（6）：42－46．

［5］ Azzam R M A，Bashara N M．Ellipsometry and poliarized light［M］．Amsterdam：North－Holland Publishing Co．，1977：269．

［6］ 王洪涛．椭圆偏振法测量薄膜参量的数据处理［J］．物理实验，2001，21（7）：8－12，17．

［7］ Law B M，Pak H K．Ellipsometric imaging of surface drops［J］．J．Opt．Soc．Am．A，1996，13（2）：379－384．

［8］ Dobrowolski J A，Ho F C，Waldorf A．Determination of optical constants of thin film coating materials base on inverse synthesis［J］．Applied Optics，1983，22（20）：3191－3200．

［9］ 廖清君，王植恒，王磊，等．模拟退火法在吸收薄膜的椭偏反演算法中的应用［J］．光学学报，2002，22（6）：683－687．

［10］ 刘静．粒子群优化算法研究及其在优化理论中的应用［D］．无锡：江南大学，2007．

［11］ 王党社，张建科，徐均琪．薄膜光学常数的粒子群算法［J］．计算物理，2008，25（2）：208－212．

［12］ Ross T，Cormier G．Particle swarm optimization for ellipsometric data inversion of samples having an arbitrary number of layers［J］．J．Opt．Soc．Am．A，2010，27（2）：319－326．

［13］ Cormier G，Boudreau R．Genetic algorithm for ellipsometric data inversion of absorbing layers［J］．J．Opt．Soc．Am．A，2000，17（1）：129－134．

［14］ Comfort J C，Urban F K，Barton D．An algorithm for analyzing ellipsometric data taken with multiple angles of incidence［J］．Thin Solid Films，1996，290－291：51－56．

［15］ 周建华，游佰强，洪志哲．反射式椭偏测试系统的全局优化算法［J］．激光与红外，2005，35（3）：214－216．