不同取向的向列型液晶盒的光电响应曲线

王思齐，孟 颖，高文莉，江洪健

（南京大学 物理学院，江苏 南京210046）

1 引 言

液晶作为现代显示器的基础材料在现代显示技术中占有重要地位，其响应时间短、耗电少、工作电压低、易于操作等特性使其在光电显示领域具有巨大的优势．液晶显示器的工作原理为偏振光经过液晶分子层后其偏振态会发生改变，液晶分子类似于单光轴晶体具有双折射特性，其光轴一般认为沿着液晶分子的长轴方向．液晶分子在外电场作用下其长轴会重新排列而趋向于沿着电场方向或垂直于电场方向，亦即通过外加电场可控制液晶层的双折射现象．因此液晶也是一种空间光调制器［1］．液晶的光强透过率随电压的变化曲线是判断液晶盒优劣的重要标准．通常讨论的液晶盒主要是常用于工业生产的扭曲向列型（Twisted nematic，TN）液晶盒．本文主要讨论液晶盒前后两面摩擦取向在0°～90°之间的向列型液晶盒的偏振光光强透过率随电压的变化特性，并探讨其变化特性产生的原因．

2 实验测量

液晶盒的制作工艺中有镀膜、取向、灌注液晶、封装等几个步骤，本文中玻璃基片的取向采用摩擦取向，一面的取向与正方形玻璃基片一边平行，另一面的取向与正方形玻璃一边分别成0°，30°，45°，60°，90°角，通过改变玻璃基片的摩擦方向来改变液晶分子在液晶盒中的排列取向．

实验器材：驱动电源、激光器、偏振器、向列型液晶、玻璃基片、液晶旋涂机、光学导轨、1／4波片、万用表、光功率计、紫外光固机、离心机．

测量光路如图1所示．

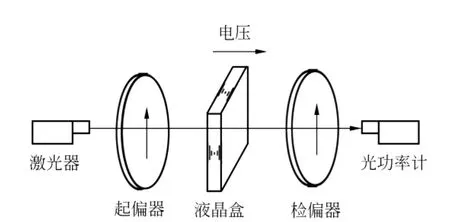
图1 实验光路图

首先选用前后玻璃基片取向垂直的液晶盒进行测量，以确定在通常情况下液晶的响应电压．调整起偏器的偏振轴方向，使光功率计读数达到最大，此时起偏器偏振轴方向与液晶盒前表面的取向方向一致，再调整检偏器偏振轴，使光功率计读数达到最大，确保检偏器偏振轴方向与液晶盒前表面取向方向也一致，将液晶盒接入驱动电源，电压调至0 V，逐渐增加电压至8 V，测得光电曲线如图2所示，可以看出液晶分子对电压的响应约从3 V开始．显然，在该情况下，液晶盒为常黑型扭曲向列相液晶盒，是工业中常用的液晶盒，其阈值电压和关断电压分别为2．8 V与4．4 V．从图2中可以看出，该液晶盒的性能较好，在0～2．8 V之间透过率始终为0；2．8～4．4 V之间透过率陡然变大，然而4．4 V之后其透过率变化缓慢，与实验中一般所测得的透过率变化曲线趋势一致．

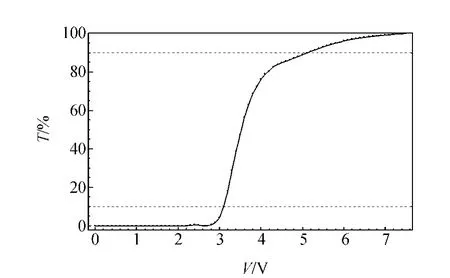
图2 普通TN液晶盒光强透过率曲线

若将起偏器旋转45°，保持偏振轴与液晶盒前表面取向方向成45°，且检偏器偏振轴方向与起偏器平行，所得透过率曲线呈现出不同的情况．将液晶盒接入电压源，电压源调整至28 V输出，此时可认为液晶分子基本沿电场方向排列，即透过率达到最大，记下此时光功率计的读数．从28 V开始缓慢降低电压至0 V，每隔0．1 V记录光功率稳定时的读数，将所得数据除以28 V时光功率计数值，可得到该液晶盒的透过率随电压的变化曲线如图3所示．

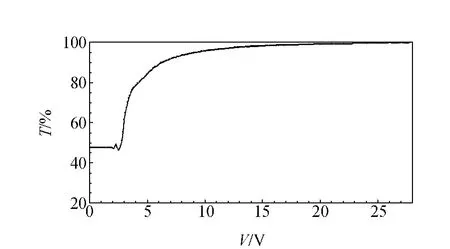
图3 TN液晶盒在45°偏振片下的透过率曲线

从图3中可以看到在3 V时液晶的透过率与图2中变化趋势不同，而出现小幅度振荡．电压从0 V增加时，液晶盒的透过率在3 V之前几乎不变，接近3 V时先稍增加再减小，随后出现了陡然增加，透过率迅速增大，5 V之后透过率增大放缓，直至不变．对液晶分子随电压的变化情况作如下分析：在0～3 V液晶盒对电压变化基本没有响应，此时液晶分子仍然沿原取向方向排列，由于电压过小，液晶分子受到电场的作用较小；在3～5 V的电压范围内，液晶分子开始对电压产生响应，这一段的响应与图2中平缓变化不同，呈现出小幅度波动，在同样条件下做了多次均有此波动现象．小幅振荡之后的曲线对应于图2中透过率在两阈值电压之间增大的一段，与正常情况下液晶盒的电光效应曲线一致．按照液晶的工作原理，随着电压增大，液晶分子沿电场排列的比例增大，出射光中沿原偏振方向投射的光所占比例应当增大，而不会出现图3中所见波动．为进一步研究这一振荡情况，对平行取向的液晶盒进行测量，同样保证起偏器与检偏器平行且与液晶盒取向方向成45°，得到如图4所示情况．

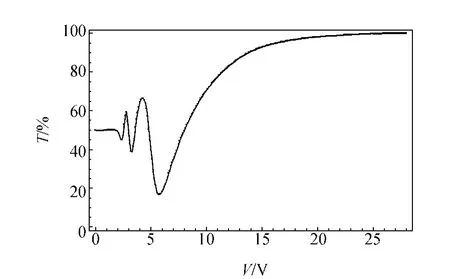
图4 平行取向液晶盒在45°偏振片下的透过率曲线

从图4可以看出在3 V附近的透过率振荡现象明显加强，且呈现出多次波动的现象，同时波峰的数目增加．由于玻璃基片的取向难以做到完全平行，波峰的个数2片并不一致，但振幅随着电压的增大而增大的趋势是统一的．对比图3中垂直取向的图像，该现象可能与液晶盒的取向方向有关．猜测这种相关性为负相关性，即液晶盒前后两玻璃基片的摩擦取向角度在0°～90°之间越大，则在相应电压附近液晶盒透过率的变化越小．

对45°取向的液晶盒进行验证可得图5．其透过率在响应电压附近的振荡振幅正好处于0°取向和90°取向的情况之间，且波峰的个数也介于2种情况之间，图5中第二个波谷明显大于第一个波谷，可见，靠近0 V的波动随着角度的增大呈现出减弱的趋势．

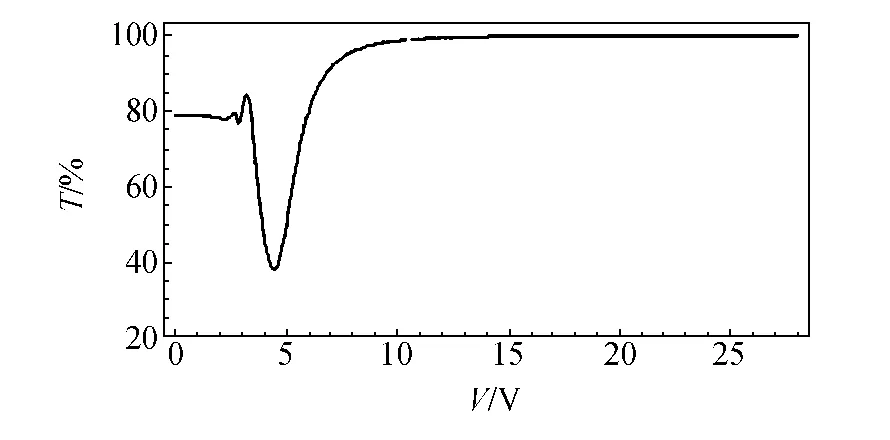
图5 45°取向液晶盒在45°偏振片下的透过率曲线

以上讨论均是对每一种情况保证检偏器偏振轴方向与液晶盒前表面玻璃基片成45°进行的，而由于每一液晶盒的前表面取向可能稍有不同，对每一液晶片进行测量时，起偏器与检偏器的偏振轴方向是不同的，为进行更精确的验证，取前后偏振器的偏振轴与竖直方向夹角45°，保持同样的情况进行测量，对30°和60°取向的液晶片的实验结果如图6所示．

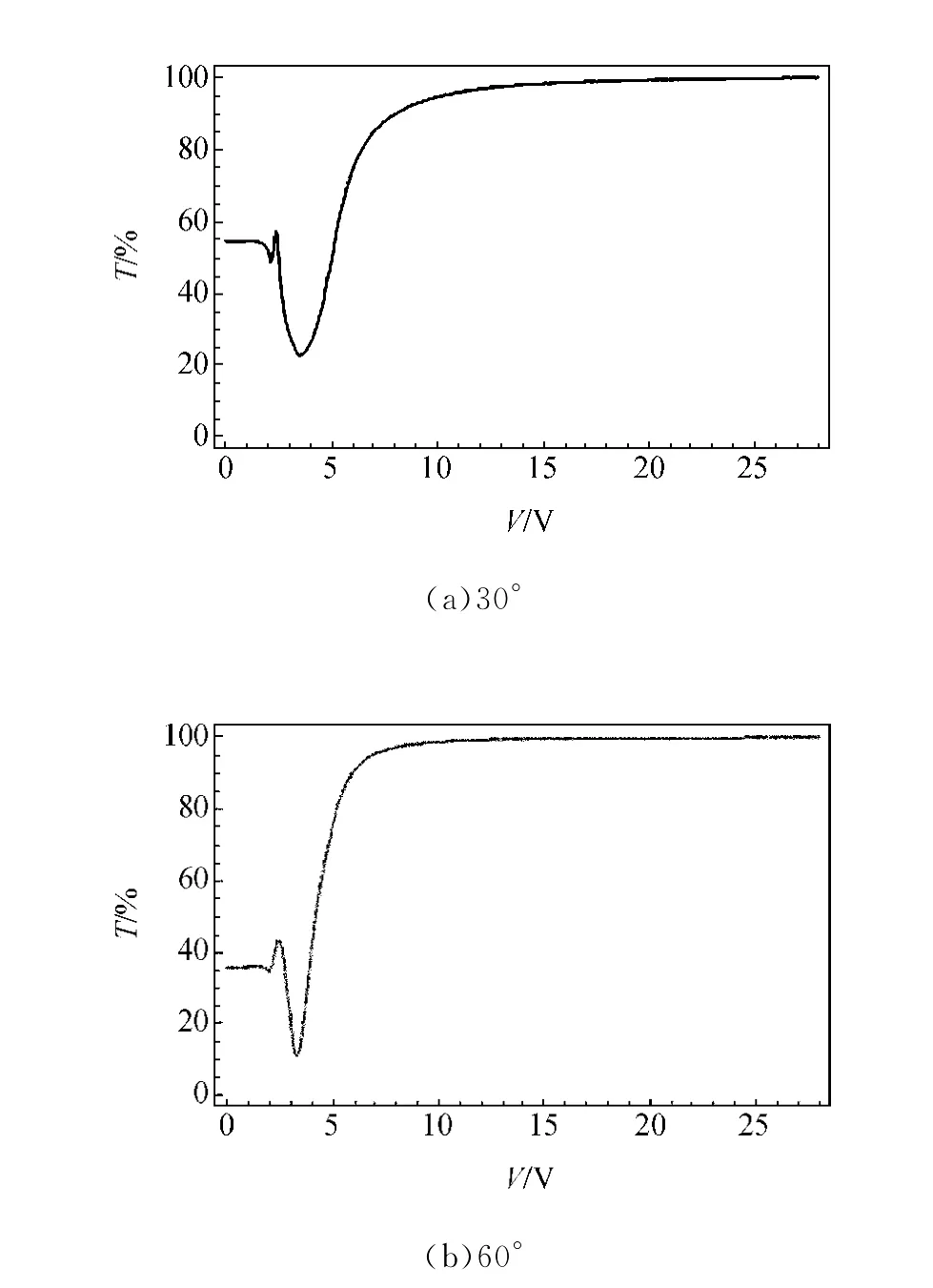
6 30°与60°取向液晶盒在45°偏振片下的透过率曲线

3 结果分析

从实验结果中可以看出，对不同取向的液晶盒其透射率随电压变化的曲线均在阈值电压附近存在振荡，且这种振荡随取向角度变化具有如下规律：随着前后2片液晶片取向所成角度的减小，振荡峰值个数表现出增加趋势，且振幅逐渐加大，透过率达到稳定状态时对应的电压也逐渐增大．以下定性地分析这种现象产生的原因．

对于向列型液晶，分子在长轴的方向排列致密，而与之垂直的方向排列稀疏，这种性质称为单轴各向异性，因为这种性质的存在，可以将定向排列的向列型液晶等效成单轴晶体．向列型液晶的光轴沿分子长轴方向，对不沿光轴射入的光，向列型液晶具有双折射作用．即折射光将分为2束，一束遵守折射定律，无论入射光束的方位如何，这束光总在入射面内，称为寻常光，用o来表示；另一束则不遵守折射定律，因此称为非寻常光，用e来表示．

e光和o光在液晶中传播的折射率可以用折射率椭球来描述［2］，如图7（a），z轴方向与液晶取向矢方向一致，n⊥＝nx＝ny，n‖＝nz．对于与光轴成θ角入射的束光，由图7（b）易知其折射率关系可以表述为

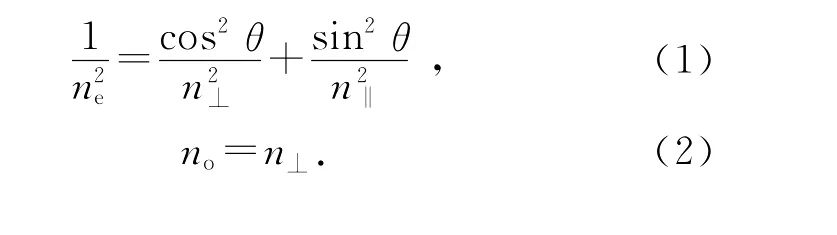
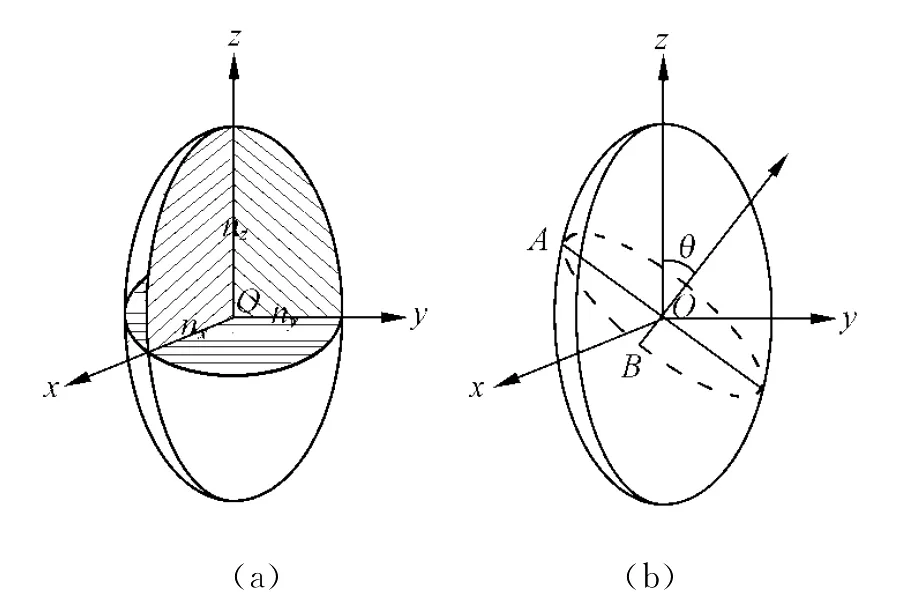
图7 折射率椭球

本实验中观察到的振荡具有如下性质：光功率的极大值的个数m是由液晶分子从初始取向角转到与外场垂直过程中相位角δ的变化与π的比值来确定的，即

式中d为液晶片的厚度．

上述公式在入射光为单色光的情况下适用，本实验过程采用的是白光，假设该公式是近似适用的，可以如下考虑：折射率的变化与入射光的波长有关，折射率与波长的比值减弱了这种影响．当然，这种近似是粗糙的，却能够说明出现振荡的原因．而且可以推测，全波段光对图像的影响是对振荡的削弱作用，这也可以解释实验中得到的图像与文献中相比振荡较弱［3－5］．

由上述分析可知，出现振荡是因为n‖与n⊥的变化，n‖和n⊥与no和ne的变化密切相关，同时no和ne的变化意味着液晶光轴的变化．因此，对于不同取向的液晶盒光强透射率随电压的变化存在振荡的现象可以如下解释：液晶分子的排列随电压的增加，其长轴取向逐步发生变化，导致液晶盒的等效光轴发生改变，造成出射光的偏振态改变，影响了出射光在检偏器方向的投影大小，故光功率出现振荡．

更进一步研究表明，这种影响存在一定的规律．取平行取向的向列相液晶，外加电压从0 V变化到10 V，每隔1 V记录1次数据，每个电压下将检偏器转动1周，每隔10°读出光功率计的示数．为保证图像的明晰度，现选取3，6，9 V所得数据在极坐标系下将光功率对检偏器的角度作图如图8所示．

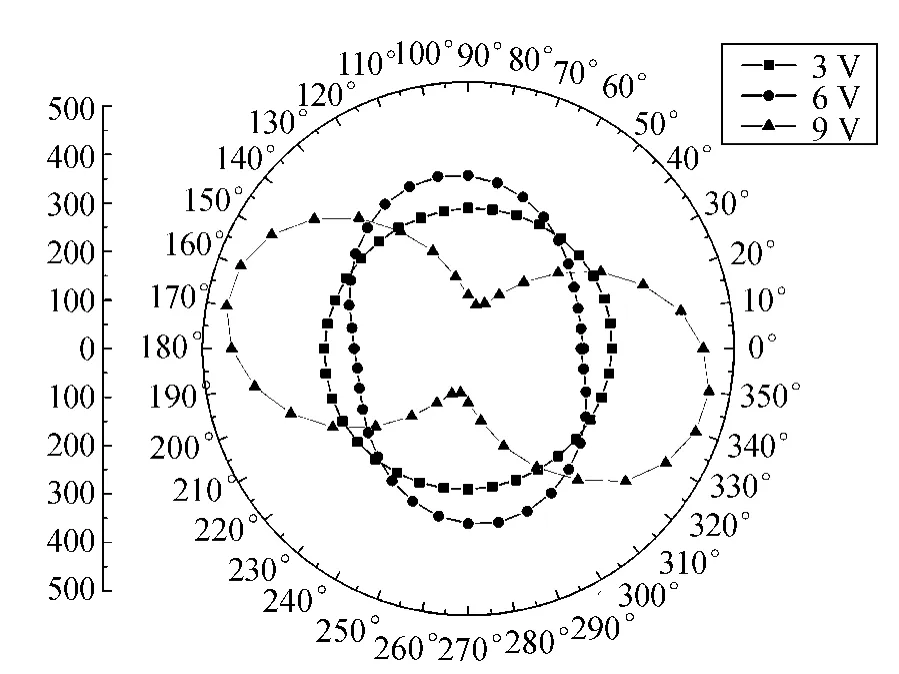
图8 光强随检偏器角度变化

对出射光的偏振态研究如下．如图8所示，所有出射光均存在2个极大和极小的光强方向，若出射光为椭圆偏振光，则将椭圆偏振光表示为2个方向的分量可得：

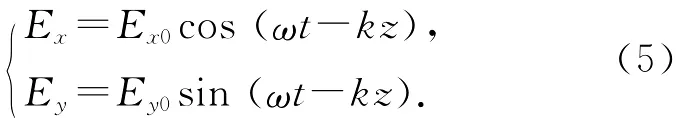
分别将2个分量投影到与长轴成α角的方向上，

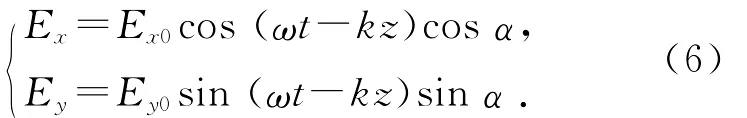
则该方向上的光强可表示为

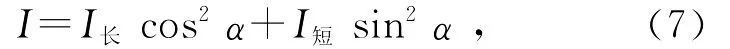
其中I长与I短分别为实验中所测得的在每个电压下光功率的最大值和最小值，极坐标系中利用实验中测得的长短轴数据以及长轴的倾斜角度，对I做关于α的图像（图9），与原图像进行对比．可见，在假设椭圆偏振光的情况下所得到的各方向光强的分布与实验中实际测量得出的结果是相一致的，亦即出射光为椭圆偏振光的假设是正确的，同时如图8所示，椭圆偏振光的偏振状态的确随着电压的变化而在不断改变，其长短轴方向以及极大、极小光强也在逐渐变化．

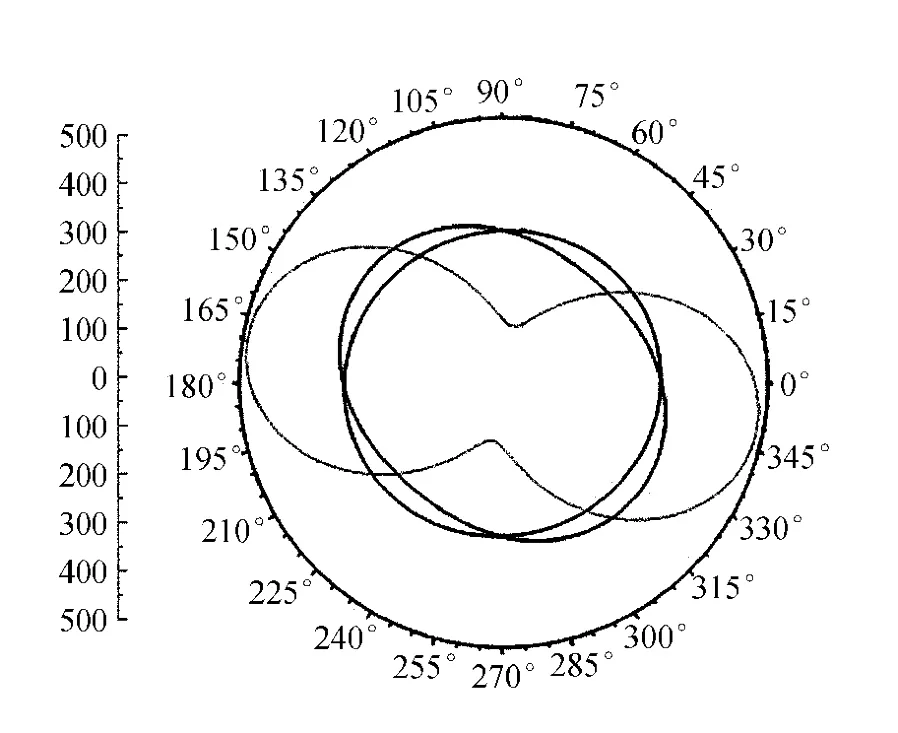
图9 理论上光强随检偏器角度变化

而出射光的偏振态在不断变化，即光矢量在不断变化，应是由于液晶盒的等效光轴的变化引起的．如果将椭圆偏振光长轴方向的变化等效为液晶光轴方向的变化，其角度及出射极大光强取值随电压的变化如图10和图11所示．

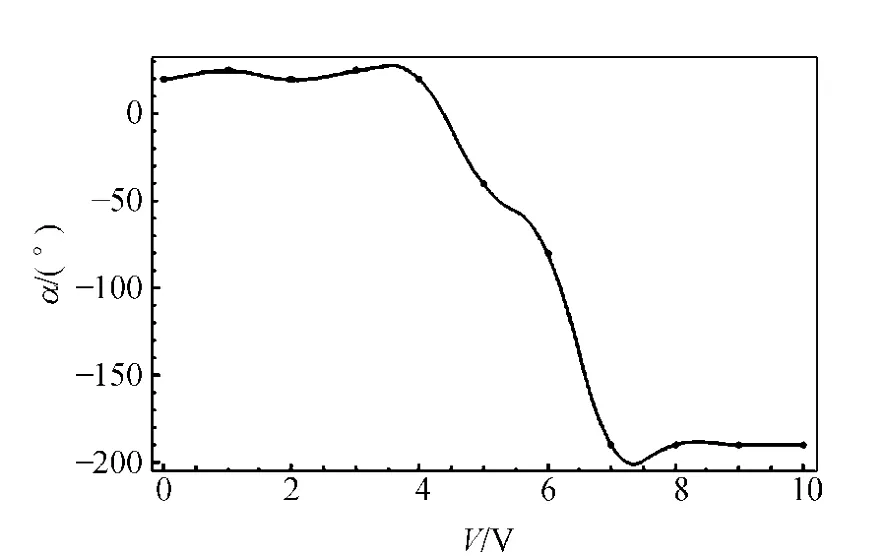
图10 椭圆偏振光长轴随电压变化图

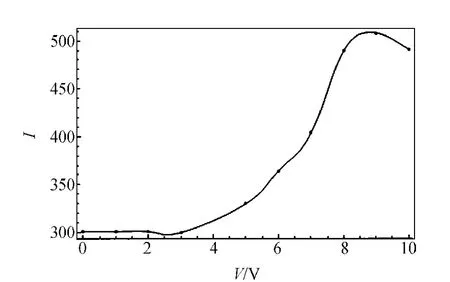
图11 椭圆偏振光极大光强随电压变化图

如图10所示，当液晶开始有明显响应时，透过液晶盒出射的椭圆偏振光长轴开始快速转动，之后其变化变得平缓，椭圆偏振光的变化可等效地看作液晶盒内光轴的变动，这种转动引起了投影在检偏器偏振方向光强的非单调变化．与之对比，长轴方向的光强确实是在逐渐增强的，且这种递变规律符合液晶盒电光响应曲线的突变特性．因此，平行取向的液晶片在电压增大的过程中光轴产生转动，而在一般的测量过程中，检偏器与起偏器均保持不变，故所测的光强值为某一方向的投影，随着光轴的转动，在这一特定方向的投影会产生非单调的变化，故在电光曲线中出现比较大的起伏振荡，而在接近一般液晶盒的阈值电压时，液晶分子在电场作用下转动放缓，随之引起液晶盒的等效光轴变化缓慢，故这一段曲线与标准测量得到的上升阶段曲线基本一致．

实际上，液晶盒光轴的变化所引起的是出射能量在各个不同方向的分配产生变化，将出射的偏振光等效表示为两正交光矢量之和，则出射总光强可以表示为

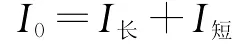
将I0关于电压作图可得图12．

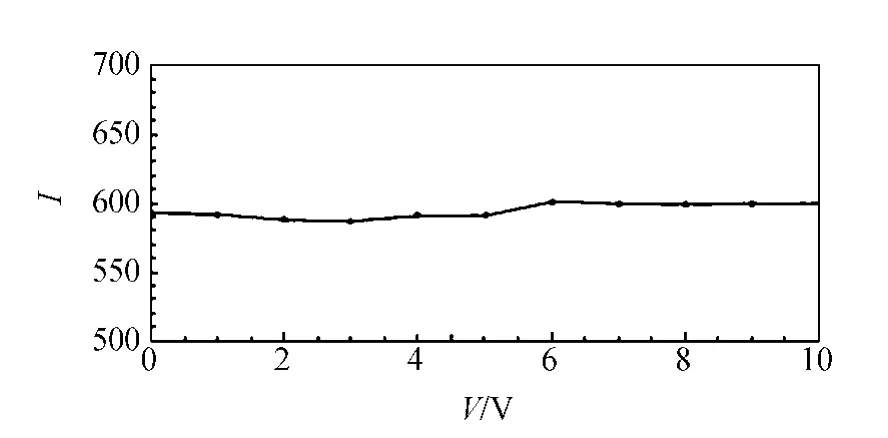
图12 总光强随电压变化曲线

从图12可以看出，总光强几乎不随电压发生变化，故液晶分子对于光的吸收在各电压下基本保持一致，只是出射光在各个投影方向的光强分布随着电压的变化而产生变化．

综上所述，有如下结论：向列相液晶盒的电光曲线中出现振荡的原因在于随电压增加，液晶分子的长轴取向发生改变，导致通常所选取的液晶盒等效光轴发生的变化，因此出射的椭圆偏振光的长轴、短轴方向改变，能量在空间中各角度的分布也发生变化，而检偏器的方向一般在测量过程中是不会改变的，因而出射光功率呈现出上下波动的非单调变化．同时，在增大电压的过程中，光轴的改变逐渐放缓，因而出现图像中的振荡逐渐减小的现象．由图2～6可以看出，波动呈现出随角度的增大而逐渐减弱的趋势，这是由于不同取向的液晶盒对液晶分子的作用效果不同，随着液晶盒取向角从0°增加到90°，盒中液晶分子的排列是逐渐趋向于有序的．理论上液晶盒内的液晶分子在靠近玻璃基片时是沿着基片上的摩擦刻痕排列的，中间的液晶分子排列呈现出递变规律．而实际上，液晶盒的取向越靠近90°，盒内的液晶分子排列才越靠近理想的状况．作为对比，未取向的液晶盒在相同情况下的透过率曲线如图13所示．可见，未取向的液晶盒透过率与平行时的情况相似，而与90°取向时的相差巨大．在其他角度时，由于盒内液晶分子并不完全按照理想情况排列，在电压增加时，随着液晶分子在电场作用下转动，液晶盒的等效光轴出现的转动情况与取向角度呈负相关关系．故才有图2～6所示的规律产生．

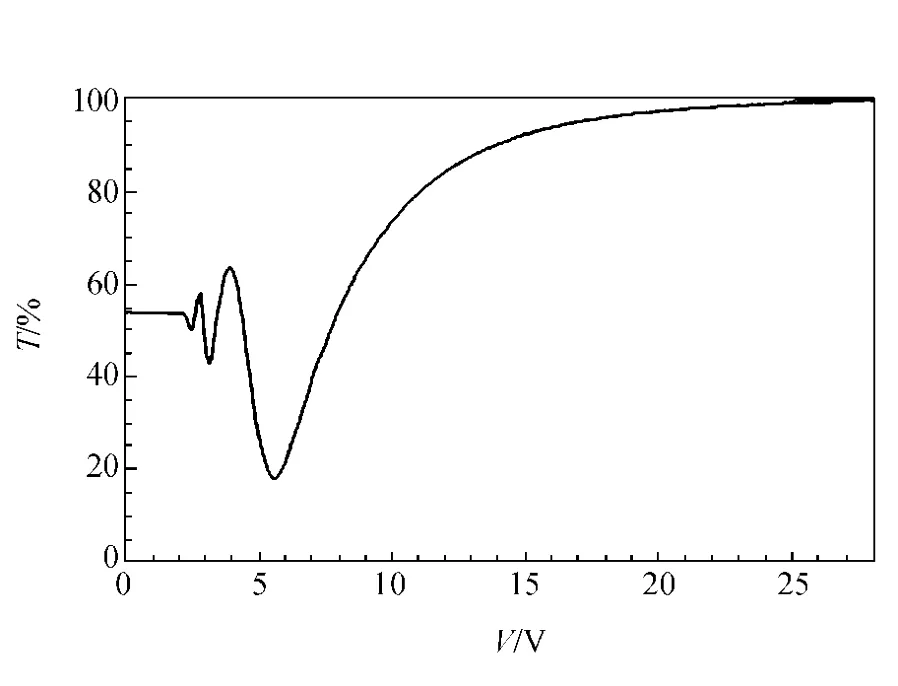
图13 未取向液晶盒的透过率曲线

作为验证，测量液晶片取向角为90°的椭圆偏振光情况，电压取3 V和28 V时出射光光强投影随角度的变化如图14所示．与图8对比，垂直取向液晶盒得到的出射椭圆偏振光其长轴旋转的角度较小，故在图3中仅表现为很小幅度的波动，这与前文理论上的解释的是相一致的．

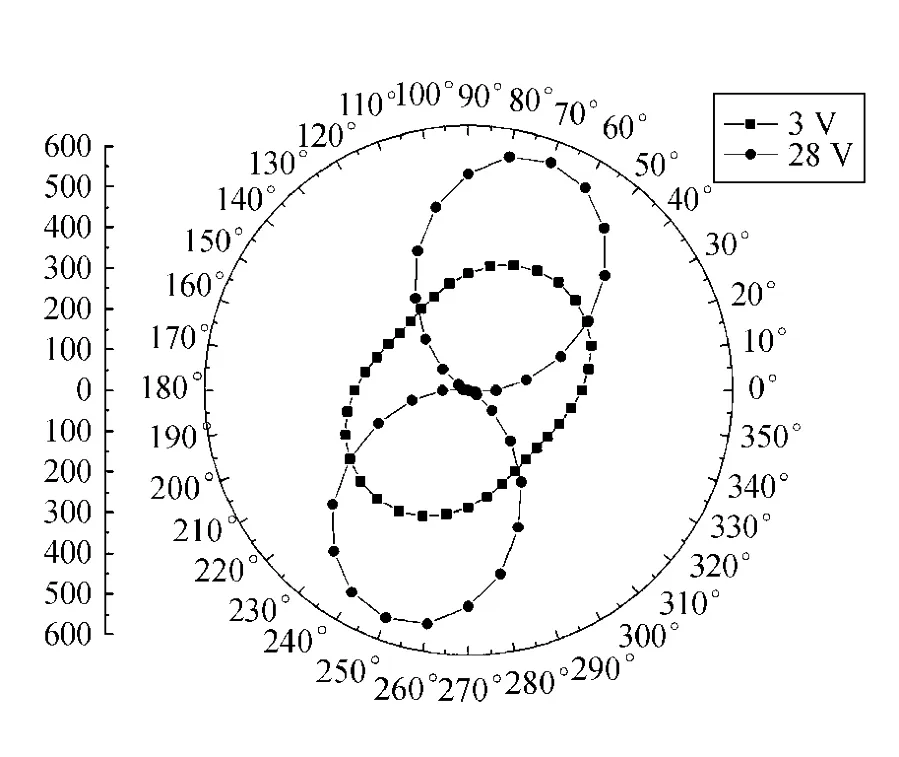
图14 垂直取向光强随检偏器角度变化

4 结 论

由实验中观察到的平行取向向列型液晶片相应电光曲线存在振荡开始，测得了60°，45°，30°和平行取向的向列型液晶盒的光强透过率随电压变化曲线，发现这种振荡随取向角的减小而数量增加而且趋于剧烈．通过实验可以证明，这种起伏振荡是因液晶分子在外加电场作用下其取向变化导致液晶盒的等效光轴的变化引起的，随着电压的增加，液晶盒的等效光轴呈现先迅速转动然后趋于平缓的变化趋势．在这一过程中，检偏器的角度始终没有改变，造成投影在检偏器透光方向的光强随着电压呈现出非单调的变化．此外，液晶盒等效光轴的变化随取向角增加而减小．因此，垂直取向的向列型液晶盒的光强投射率随电压的变化情况是最稳定的，适宜在工业生产过程中采用．

［1］ 陈嘉琦，傅晓，苏为宁，等．向列型液晶盒的光电响应特性［J］．物理实验，2011，31（9）：41－44．

［2］ 黄子强．液晶显示原理［M］．北京：国防工业出版社，2008：80－83，26－127．

［3］ 杨桂娟，康冬梅．90°扭曲向列型液晶的电－光开关特性［J］．内蒙古民族大学学报：自然科学版，2006，21（3）：264－267．

［4］ 王必利，王慧．向列相液晶电光特性研究［J］．大学物理实验，2011，24（2）：4－6．

［5］ 王宁，李国华，云茂金，等．液晶电控双折射特性的研究［J］．中国激光，2002，29（12）：1064－1066．