固体密度的测量

2012-01-26俞晓明

物理实验 2012年9期

俞晓明，陈辉

（盐城工学院a．基础教学部；b．机械工程学院，江苏盐城224051）

1 引言

密度是材料基本物理性质之一，其测量在理论和工程上都有着重要的意义．密度ρ为其质量m与体积V之比，即

因此，准确测量质量m和体积V成为关键．m的测量一般转化为力的测量，如文献［1］等利用托盘天平实质是等臂杠杆来测量力；文献［2］等利用焦利秤来测量力；文献［3－5］等通过传感器将力的测量转化为电压的测量．固体V的测量可分为3类：其一，对规则固体采用长度测量工具测量诸如直径、长度、厚度等物理量，然后计算出体积．其二，对不规则且不溶于水、不吸水或与水不发生化学反应的固体，若其密度大于浸入液体，采用流体静力称衡法［6－7］，即根据阿基米德原理采用排空法测量体积；若密度小于浸入液体，则可绑缚密度较大的固体后再采用流体静力称衡法［2，8］．其三，对不规则但溶于水、吸水或与水发生化学反应以及多孔物质、粉尘物质，多数利用排气法［9－11］或排沙法［8，12］．

文献［13］根据“物体排开水的重力与它的重力之比等于动力臂与阻力臂之比”，通过将“被测物体挂在密度秤左端，接水袋挂在密度秤的右端”，设计了固体密度秤．本文在此基础上，改进了实验装置和步骤，应用杠杆原理、阿基米德原理和已知温度下水的密度公认值，测得了密度大于水的石块和小于水的木块的密度，整个过程无需用接水袋接水，操作方便．

2 石块密度的测量

2．1 实验装置及步骤

实验装置如图1所示．

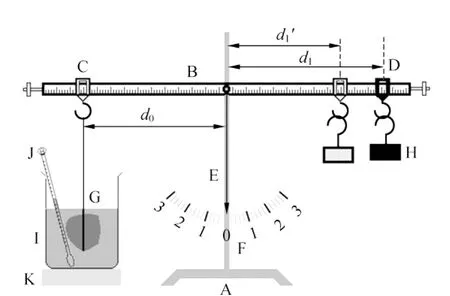
图1 测量固体密度的实验装置

首先，将细线的一端拴住石块，另一端系在铁架台A的转轴上，在铁架台转轴下方安装量角器F并使其“0”刻度与拴住石块的细线对准（石块用作铅垂仪）．解离细线和石块，将长直指针E垂直固定在杠杆上，在杠杆的轴处涂上适量润滑油，安装杠杆并调节两端的平衡螺母直至指针E指向量角器F的“0”刻度，此时杠杆水平．接着，将用细线拴着的石块G系在杠杆左端的挂钩C上并固定挂钩C，移动右侧挂钩D与钩码H至指针指“0”，读出此时挂钩C的读数d0、挂钩D的读数d1．然后，将盛水的烧杯I放在石块下方，调节垫板K的高度，使石块G浸没水中（保持挂钩C的读数d0不变），调节杠杆右侧挂钩D，使指针再次指“0”，读出此时挂钩D的读数d1′．读出温度计J的读数．

改变挂钩C的位置，重复相关实验步骤，多次测量，取平均值．

2．2 实验原理

设石块的质量为ms、体积为Vs，钩码的质量为mp．当石块未浸入水时，根据杠杆原理有

当石块全部浸入水时，有

式（3）中ρw为水的密度．水的温度可由温度计J读出，该温度下其密度公认值可从手册查出．由式（1）～（3）计算出石块的密度ρs为

2．3 实验数据

利用固体密度测量装置测得的实验数据如表1所示．通过计算可以得石块的¯ρ测＝2．63×103kg·m－3，测量温度为20℃．实验中由于石块的材质不同，密度没有公认值，为此用同样的方法继续测量铁柱的密度为¯ρ测＝7．74×103kg／m3，测量温度为22℃．实验所用的铁柱为规则物体，用游标卡尺测量其内外径和高度，用天平测量质量，测得ρ测′＝7．86×103kg／m3，两者误差δ＝1．53%，这表明采用该方法测量石块质量密度可行，所测结果可信．

表1 石块与铁柱密度的测量数据

3 木块密度的测量

3．1 实验方法与步骤

木块密度小于水的密度，不能全部浸入水中，将密度较大的钩码绑缚于木块的下端，使其浸没水中．

首先，调节杠杆螺母，使杠杆水平．将木块绑缚于细线的中间，细线的一端系在杠杆左侧的挂钩C上，移动右侧挂钩D，使指针指“0”，读出此时挂钩C的读数d0、挂钩D的读数d1．接着，将另一钩码绑缚在木块的下方，将烧杯I放在钩码和木块的正下方，保持挂钩C的位置不变，调节垫板K的高度，向烧杯中加入适量的水，使钩码浸没在水中（此时木块尚未接触水面），调节杠杆右侧挂钩D，使指针指“0”，读出挂钩D的读数d1′．最后，继续向烧杯中加水，使钩码和木块都浸没于水中，调节挂钩D，也使指针指“0”，读出此时挂钩D的读数d1″．注意：整个过程中不得使木块下方的钩码接触烧杯底部．

改变挂钩C的位置，重复上面的实验步骤，多次测量，取平均值．

3．2 实验原理

设木块的质量为mt、体积为Vt．当左侧只有木块时，根据杠杆原理有

当石块浸没在水中而木块仍处在空气中时有

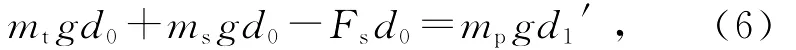
式（6）中Fs为石块浸没在水中时所受的浮力．

当石块和木块都浸没于水中时有

由式（1）和式（5）～（7）得木块的密度为

3．3 实验数据

经测量，得到如表2所示的实验数据，经计算得¯ρ测＝0．653×103kg·m－3，测量温度为23℃．

表2 木块密度的实验数据

4 实验现象与误差分析

实验时发现：1）石块密度的测量与杠杆右侧使用钩码的形状、质量无关，可用质量相当的任意配重代替；木块密度的测量与使木块能够浸入水面的钩码的形状、质量等也无关，亦可用密度大于水的配重代替．2）石块－木块密度的测量均与杠杆左侧挂钩C的位置d0无关；且同一物质测量密度时，d0／d1的3次测量结果变化不大，与理论分析结论一致．

实验产生的误差主要有：1）空气对石块和木块有浮力作用；2）空气的流动、石块和木块悬挂时的微小摆动以及杠杆轴处的摩擦等也有影响．

5 结束语

利用杠杆原理和阿基米德原理，避开质量和体积的测量，测得了密度大于水的石块和小于水的木块的密度．该方法对实验器材的要求不高，教师可在学生探究过“长度和时间的测量”、“物体的质量与体积之间的关系”、“影响物体所受重力大小的因素”、“浮力的大小”和“杠杆的平衡条件”的基础上，设计成学生课外探究的实验选题，以启发学生思维、开阔学生视野，培养学生创新意识，更好地体现《物理课程标准（实验稿）》［14］“通过实验理解密度的概念”的要求．

［1］刘炳升，李容．物理（8年级下册）［M］．南京：江苏科学技术出版社，2005：2－8．

［2］胡平亚，胡凌云．固体和液体密度测定实验的改进［J］．大学物理，1999，18（8）：28－29．

［3］陈莹梅．用半导体应变计精确测量固体和液体的密度［J］．实验技术与管理，2006，23（9）：42－44．

［4］王连加，康伟芳．应用半导体测力计测量固体和液体的密度［J］．辽宁大学学报（自然科学版），2007，34（1）：28－29．

［5］刘泓，乔亚力．固体和液体的密度电测量实验方法的研究［J］．大学物理实验，2009，23（2）：53－55，61．

［6］刘映栋．大学物理实验教程［M］．2版．南京：东南大学出版社，1998：41．

［7］何捷，陈继康．基础物理实验［M］．南京：南京师范大学出版社，2003：27．

［8］胡毅，周平．浸润性固体密度的测量［J］．绥化学院学报，2005，25（2）：161－162．

［9］青一平．可溶性固体微粒密度的测量［J］．物理实验，1994，14（6）：278－279．

［10］郭长武，张爱莲，刘玉凤．利用气体状态方程精确测定固体密度［J］．分析仪器，2001（4）：17－18．

［11］俞晓明，崔益和．绝对零度与可溶性物质质量密度的等压膨胀法测量［J］．物理实验，2011，31（10）：36－39．

［12］安爱芳，王玉清，任新成．吸水固体密度的测量［J］．延安大学学报（自然科学版），1997，16（2）：82－84．