精心设置悬念 提高思维能力

●

(宣汉县中小学教学研究室 四川宣汉 636150)

精心设置悬念提高思维能力

●赵绪昌

(宣汉县中小学教学研究室 四川宣汉 636150)

中国古代的章回小说往往在读者最激动、最关注的地方来一个“欲知后事如何，且听下回分解”.悬念是一种学习心理机制，它是由学生对所学对象感到疑惑不解而又想解决它产生的一种心理状态.悬念的设置，能激发学生的学习动机和兴趣，使学生思维活跃、想象丰富、记忆加强，并有利于培养学生克服学习困难的意志力.教师在课堂教学中，要善于捕捉时机，恰当设置悬念，以拨动学生探索新知识的心理，提高课堂教学效益.

1 课始设悬念，学习添情趣

俗话说，良好的开端是成功的一半.教师在讲授新课之前，先设置悬念，可以触发学生的求知动机，产生一种非知不可的紧迫心情，形成认知“冲突”.“冲突”一旦形成，学生的注意力最集中，思维处于最积极的状态.正如托尔斯泰所说的,成功的教学所需的不是强制，而是激发学生学习的兴趣.

案例1对初中未学过对数的高中学生来说，对数概念及运用显得枯燥乏味.为引发学生的学习兴趣，在介绍对数之前，笔者出了一道趣味问题：“某城市有800万人口.现在有一人带来一个好消息，在该城市传播.若每隔一小时，每个知道此消息的人都传播给另外2个人.问一昼夜间这个消息能传遍全城每位居民吗?”

一开始，学生们皆认为不大可能.这时，笔者引导学生计算：1小时后，有1+2=3(=31)人知道好消息；2小时后，有1+2+6=9(=32)人知道好消息；3小时后，有“1+2+6+18=27(=33)人知道好消息.猜想，n小时后，有1+2+6+…=3n人知道好消息.那么当n≤24时，能有3n>8 000 000成立吗?

学习了对数之后，能用最简单的方法解决此问题.学生们带着这个悬念，开始津津有味地进入对数课的学习.

案例2在讲授“面面垂直判定定理”时，笔者设计了这样的悬念：“建筑工地上，泥水匠正在砌墙.为了保证墙面与地面的垂直，用一根吊着铅锤的绳来看看细绳与墙面是否吻合.如此，能保证墙面与地面垂直吗？泥水匠或许不知道其中的奥秘，你能找到理论依据吗？”

在这种情况下，教师的讲课就会像磁石一样牢牢地吸引住学生的注意力，学生的思维活动和情绪也和教师的讲课交融在一起，使所讲授知识溶解于学生思维的潮水之中.

2 课中设悬念，学习见深度

在课堂教学中，教师除了要顺理成章地进行新课讲授外，还要有目的、有意识地设置悬念，拓宽学生的思维，使学生学有所思、思有所得，以达到举一反三的效果.

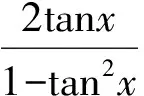
通过教师精心设置悬念，引导学生释疑，学生真正领会定义域对周期的制约作用.

案例4已知正方体ABCD-A1B1C1D1(如图1)，求半平面B1BD1和半平面C1BD1所成二面角的大小.

生1：构造二面角的平面角.

分析BD1是二面角的棱.分别在题设的2个半平面内作C1E⊥BD1，B1F⊥BD1，垂足依次为点E，F，很明显E，F是BD1的三等分点，因此∠B1EC1不是所求二面角的平面角，应设法平移B1F.

设A1C1∩B1D1=O1，则O1E∥B1F，又O1E⊥BD1，于是∠O1EC1是二面角B1-BD1-C1的平面角，求得∠O1EC1=60°(过程略).

受到图形的启示，第2个同学给出了更简明的解法.

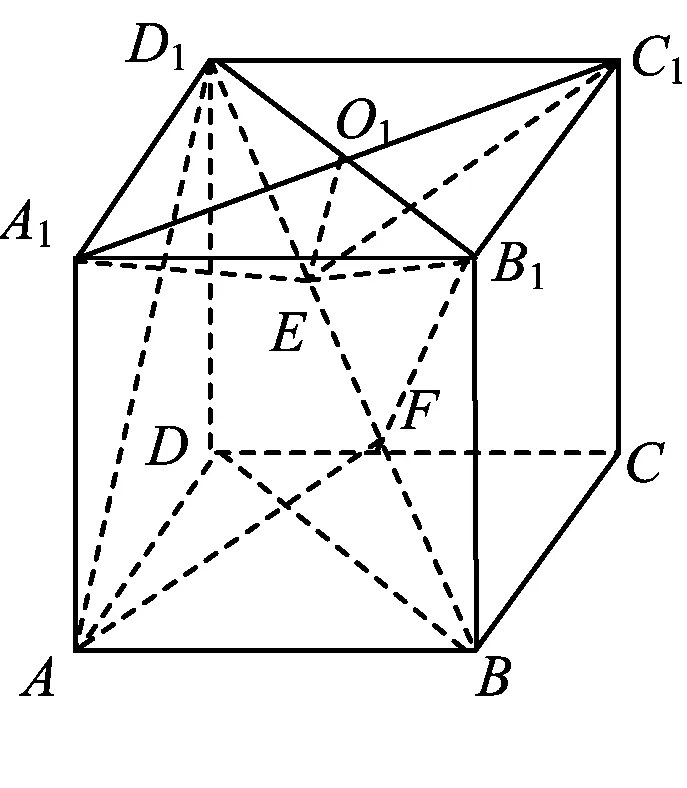
图1

生2：如图1，可证A1C1⊥对角面BDD1B1，作C1E⊥BD1于点E，连结O1E.由三垂线定理的逆定理，得EO1⊥BD1，于是∠O1EC是所求二面角的平面角.以下过程略.

受A1C1垂直对角面的启示，有同学给出了对称的设想.

生3：因为A1C1⊥对角面BDD1B1，作C1E⊥BD1于点E，连结A1E.由△A1D1E≌△C1D1E，得A1E⊥BD1，于是∠A1EC1是二面角A1-BD1-C1的平面角,易求得∠A1EC1=120°.考察正方体的对称特征，发现二面角B1-BD1-C1与A1-BD1-B1的平面角分别是∠O1EC和∠O1EA1，且∠O1EC=∠O1EA1，因此二面角B1-BD1-C1为二面角A1-BD1-C1的一半，即所求二面角的大小为60°.

受生3的启迪，有同学给出了延伸面的设想.

生4：半平面ABD1是半平面C1BD1的延伸面，它们与半平面B1BD1构成的2个二面角互补.作B1F⊥BD1于点F，连结AF.同生3，可证∠AFB1是二面角A-BD1-B1的平面角，并求得∠AFB1=120°，故所求二面角的大小为60°.

限于篇幅，其他方法不再列出.

以悬念为导火线点燃思维的火花，促使思维的灵感相互触碰，开拓思路，有效地提高学生独立分析问题、解决问题的能力.

3 课末设悬念，学习泛余波

教师在课堂收尾时，提出一些富于启发、思考的问题，但不作答复，造成悬念，则有“欲知后事如何，且听下回分解”的魅力，使学生感到余味无穷，从而激发他们继续学习的热情.

案例5讲完等差数列后，下节课要学习等比数列，在结束时教师提出：假设有很大一笔资金要贷出去，并且贷出去，这钱就给你了，不过每次给你钱，你得返还笔者一定数额的钱.第1天贷给你100万元，你得返还笔者1元；第2天贷给你200万元，你得返还笔者2元；第3天贷给你300万元，你得返还笔者4元，依此类推，每次返还的钱是上次的2倍，一直到30天，交易结束.你敢签这份贷款协议吗？这时学生马上活跃起来，有的在一天一天地算下去，有的企图寻找规律.这样，学生一定很想知道其中的奥秘，急切地等着下一节课，并为上好下节课做好铺垫.

总之，悬念的设置是课堂教学中的一种技巧.它可以吸引学生的注意力，提高学生学习的兴趣，增强学生提出问题、分析问题、解决问题的能力.当然，悬念的设置必须新颖、实际、简捷、恰到好处.课堂教学中为学生设置的悬念是以学生易于了解的实际事例、又能启发大多数学生积极思维、经过努力能够回答的问题为好.

[1] 赵绪昌.设置悬念，提高效益[J].中小学数学(初中版)，1995(1)：1.

[2] 臧立本.如何激发思维灵感[J].数学通报，2008(6)：22-23;25.

[3] 陆联英.数学教学中多元性问题的设计[J].上海教育科研，2008(3)：70-71.