例析“5+4+2”解题算式及其教学

●

(南京师范大学数学科学学院 江苏南京 210046)

例析“5+4+2”解题算式及其教学

●胡玉霆

(南京师范大学数学科学学院 江苏南京 210046)

如果说正确解题能够使学生获得成功的喜悦，那么通过解题获得的认识力对学生的帮助无疑是潜在而持久的.葛军副教授基于多年对解题教学的研究，提出“5+4+2”解题算式，转变了为解题而解题的认识，打破了就题解题的单一活动形式，形成一个以解题为载体，充分发展学生数学思维的可持续发展的动态解题系统，以期发展学生的认识力，提高学生的思维水平.

1 “5+4+2”解题算式的涵义

1.1 对“5”的解析

解题的第一步是读题.尽管不同解题者在理解题意的过程中所需要的时间不同，这取决于他们在读题过程中反复捕捉题目信息的容量大小，但对于普通解题者而言，读题过程需要5遍.

第1遍:“览”.在读题过程中，首要工作是对题目信息进行快速地文字扫描、浏览题设概貌.通过这一遍读题，解题者可以快速将题目所涉及的知识点锁定到相关范围，起到定位的作用.

第2遍:“展”.在这一遍读题中，题设中的每一个条件都将作为信息源，需要解题者逐句展开与每一个信息源相关的辐射信息.是对学生原有知识储备情况的考查，一般情况下，知识储备量越大，越有利于数学问题的解决.因此，在本次读题中，主要是完成搜索相关知识点的任务.

第3遍:“联”.本次读题完成的主要任务是“联接”，即各知识点的小组合、小联接.解题者通过第2遍对每个信息源的“链接”，罗列出与本次解题任务可能相关的知识远远不够，还需要将各个松散的知识点实质性的有机“联接”在一起，构成一个个小的知识模块.

第4遍:“顺”.完成题目信息的充分挖掘后，在这一遍读题中要求解题者能够运用不同的解题策略，根据已知条件和所求结论，初步形成一条可以解决当前任务的较细的解题思路.

第5遍:“善”.通过前4遍读题，大多数解题者认为已寻找到解题的思路，便匆匆提笔求解，这是危险而令人遗憾的.如果解题者每次都如此，那么他将一再错失掉养成优化解题思路和完善思维的良好习惯的机会.甚至在很复杂的题目面前，因匆忙而混沌的思维状态感到束手无策.因此，在这一遍读题中，我们要求回顾完善，以形成清晰的可生长的解题思路.

可以看出，上述读题过程环环相扣、层层深入，充分体现了读题即解题的观点和慢读题的策略.当然，不同的解题者因感知题目信息的能力不同和思维运算简缩性的差异，在读题过程中，有些解题者用不着5遍即可完成读题要求和解题任务，而有些解题者需要更多的读题时间完成解题任务.因此，我们这里所说的5遍只是一个约数，具体的读题次数将因人而异.

1.2 对“4”的解析

“4”即将解答写4遍.书写4遍的过程并不是机械的重复劳动，而是一个逐渐抽象、逐渐升华的过程.

第1遍:“粗”.解题者在对题目有了充分认识和理解后，开始着手书写表述.在第1遍书写时，需要解题者将解答过程大致地粗写下来，但应该包括能够求解的关键步骤，并不断进行规范和补充.

第2遍:“全”.在第1遍书写的基础上，这一遍表述需要解题者将解答过程清楚而简洁地完成作答，要求思路清晰、书写规范.对于不同层次的学生而言，“全”是相对的:优等生可以只写出求解过程的重要表述、主要步骤及必要结论；中等生需再现与解题相关的定理、公式和法则，解题步骤及主要的演算过程；差等生除了书写出中等生要写出的内容外，可能还需详细呈现运算过程.

第3遍:“精”.除了简单题目外，大多数题目都有多个关键步骤.在这一遍书写中，解题者需要将题目解答过程中的关键步骤写下来，这些关键步骤将反映出题目的走势和推演是如何展开的.

第4遍:“点”.用一句话简括出题目考查的核心思想和关键要点，点石成金.

同样，在书写的过程中，4遍也只是一个约数.对于数学解题能力较好的学生而言，他们可能在第1遍就能够达到完整简洁的书写解题过程的要求,而对于数学解题能力较弱的学生，可能需要更多的时间.因此，书写4遍的要求也将因人而异.

1.3 对“2”的解析

如果一个题目只有一条解题思路即可实施，那么这样的题目并不是一道好题;如果一道题目能够使具有不同解题偏好的学生通过自己擅长或熟悉的策略完成解题任务，那么这样的题目才是值得我们研究和学习的.因此，在解法上应该追求一题多解.这里的“2”是解法数量的下限，即每道题目至少要有2种解法，当我们在完成一个解题任务时，切忌不能满足现状，要多思考其他方法，以求殊途同归的效果.

2 “5+4+2”解题算式的应用

2.1 题读“5”遍

2.1.1 析“览”

浏览题目，进行初步的文字扫描.从题设可以看出，本题所涉及的是与椭圆、直线相关的问题，并由椭圆和直线的位置关系生成若干线段，所证明结论是3条线段成等比数列的数量关系.

2.1.2 析“展”

逐句断读，辐射题设信息.

(1)“在平面直角坐标系xOy中”，本句话交代了以O为原点的坐标系，体现了公众题目的规范性.

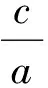
(3)“过点A作直线l交椭圆于另一点Q，交y轴于点R，直线OP平行于直线l，点P在椭圆上”，这说明直线l是如何形成的，同时点Q，R，P的关系是知道其中一个便可确定其余2个的位置.因而也交代了线段AQ，AR，OP的形成及它们之间的关系.因此可以看作由于过点A的直线l的斜率变化引起点Q，R所在位置的变化；亦可以看作由于y轴上一点R的变化引起直线l的变化和点Q的变化.但不管把哪个点看作主动因素，它们之间的制约关系决定了它们之间的数量关系不会因位置的不同而改变.

(4)“直线OP平行于直线l”，即kOP=kl，过原点O，平行于l的直线与椭圆有2个交点，这就有2种情况，但由于2个交点关于原点中心对称，即2个交点到原点的距离相等，故可任选其中一点为点P，对结果没有任何影响.

2.1.3 析“联”

在第2遍中,辐射的信息多而杂，但并不是每条信息对求解问题都有帮助，因此要根据题设条件和结论进行有目标的联接.

直线斜率为主动因素，k的变化导致点R，Q的变化，从而导致AR，AQ的变化，同时也引起了OP的变化，但其最终满足等比中项的数量关系没变；并且点Q，P既满足椭圆方程，又满足各自所在的直线方程.这2条直线又因为斜率相同而产生了紧密联系，故可以设出斜率k，分别将AQ，OP和AR表示出来.

另外，也可以换个视角将点R的坐标视为主动因素；或将点Q的坐标变化视为主动因素，将点P的坐标变化视为主动因素.依循上述思想，写出AR，AQ，OP的不同表达式，从而得到3个思想平行而结论相同的结果.

2.1.4 析“顺”

理顺前面思索的线路.设直线l的斜率为k;用点斜式写出直线l的方程;令x=0，确定直线l与y轴的交点R的坐标;表示出线段AR;将直线l与椭圆方程联立，用弦长公式得到线段AQ;已知斜率相同和原点O,得出直线OP的直线方程y=kx;将直线OP和椭圆方程联立得点P，从而确定线段OP;分别求得3条线段后，化简得AR·AQ=2OP2.

2.1.5 析“善”

在第4遍的基础上，完善解题思路的形成，并形成一条清晰的解题思路.同时可以比较第3遍中不同视角下，AQ，AR和OP表达形式的繁简情况，择出一条书写简单、计算简便的解题思路.在例1中,如果选用设点R，Q，P的坐标，再通过坐标表示出直线斜率的方法将出现分数形式，这为后续计算增添了困难，没有直接设斜率为k求解来得简便，因此优选设法仍确定为斜率k.

2.2 书写“4”遍

2.2.1 析“全”

本例省略第1遍“粗写”，从第2遍“全”开始，即完整书写出解答过程.

证明当直线斜率不存在时，不合题意.

方法1设直线l的斜率为k，则直线l的方程为

y=k(x+a).

令x=0，得y=ka，因此点R的坐标为(0，ka).又因为点A的坐标为(-a，0)，所以

又由题设得OP∥AQ，于是直线OP的方程为y=kx，从而点P满足

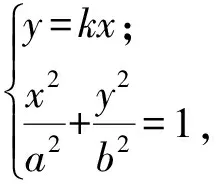
即

(b2+a2k2)x2-a2b2=0，

可得

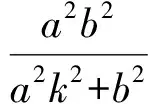
由y2=k2x2，可得

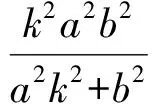
因而

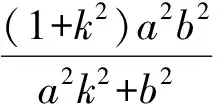
(2)

由题设得点Q的坐标满足

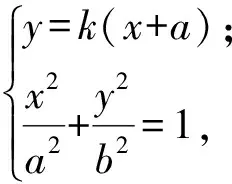
即

(b2+k2a2)x2+2a3k2x+a4k2-a2b2=0，

于是

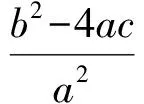
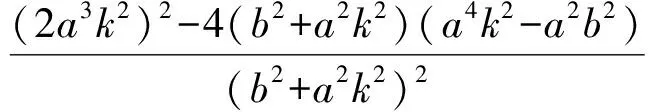
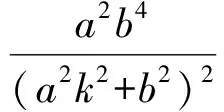
(3)

由式(1)，式(2)，式(3)得

AR2·AQ2=4OP4，

故

AR·AQ=2OP2，

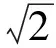
2.2.2 析“精”

本题的关键步骤有：

(1)用点斜式设出直线l的方程，即

y=k(x+a)；

(2)将直线l的方程与y轴联立得到线段AR，即AR2=(1+k2)a2；

(3)由题意设出线段OP所在的直线方程，并与椭圆方程联立得到线段OP，即

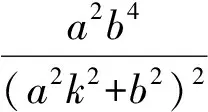
2.2.3 析“点”

“点”出题目的题眼、所涉及的知识点及解题策略.通过这一遍的简括，提炼出题目的实质和精髓，切勿让题目中的非本质信息干扰自己.

(1)直线与直线相交，AQ与y轴相交得点R.

(2)直线与二次曲线相交，OP与椭圆相交，是一条过原点的直线，得到正比例函数；AQ与椭圆相交，是一般直线方程，得到一次函数.

(3)两点间的距离公式——直线上两点的距离公式(弦长公式)，因此

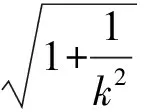
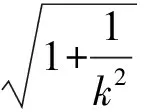
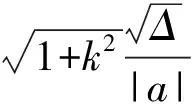
2.3 题解“2”遍

2种及其以上解法，并比较各解法的优劣.本例将分析用韦达定理和因式分解求根的优劣，以及整体化求根的思想.

2.3.1 韦达定理与因式分解

本例是一道计算型证明，需要分别算出AQ，AR，OP这3条线段的模，其中AQ的模最复杂.题目条件是已知点A的坐标(-a，0)以及直线方程和曲线方程，只需再求出点Q的坐标，进而算出线段AQ，联立方程后，得到点A,Q的横坐标(纵坐标)是以x(y)为未知数方程的2个根.当其中一点的坐标已知时，一定可将方程化成2个根式，即(x-x1)(x-x2)=0或(y-y1)(y-y2)=0，从而求出另一根.

当然，也可以用韦达定理求解，将两根之和或两根之积表示出来，再求另一根.在具体题目中，2种方法的选择没有固定要求，因题而异.在本例中，采用因式分解的方法更适宜.

(1)因式分解法.由

消去y得

即

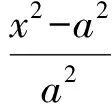
提出公因式(x+a)，可得

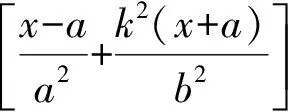
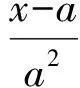
解得

(2)韦达定理法.由

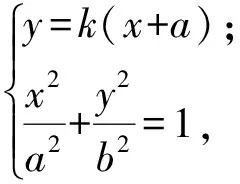
消去y得

整理得

因此

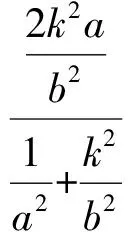
故

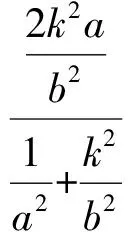
从上述2个解题过程看来，当已知2个根中的一根时，可以用因式分解求解另一个根，计算过程较之韦达定理更为简捷.

2.3.2 整体化思想

消去y得

即

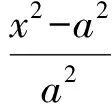
提出公因式(x+a)，可得

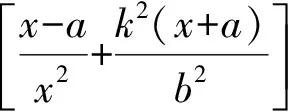
从而

故

2.3.3 其他方法

方法2设点R的坐标为(0，r)，则

且直线AR的方程可表示为

联立方程

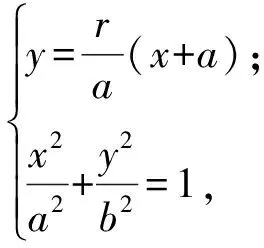
消去y得

即

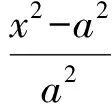
提出因式(x+a),得

由于点Q的坐标满足方程组，且x≠-a，因此

得

于是

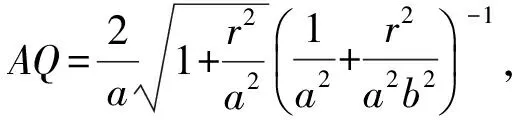
(5)

即

即

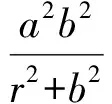
故

(6)

由式(4)、(5)、(6)可得

AR·AQ=2OP2，

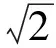
方法3设点P的坐标为(acosθ，bsinθ)，θ∈[0，π)∪(π，2π)，则

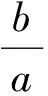
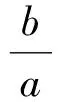
令x=0，则点R的坐标为(0，btanθ)，于是

点Q满足

消去y得

整理得

(x+a)[x-a+tan2θ(x+a)]=0，

从而

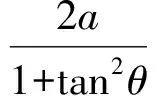
所以

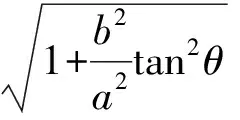
又

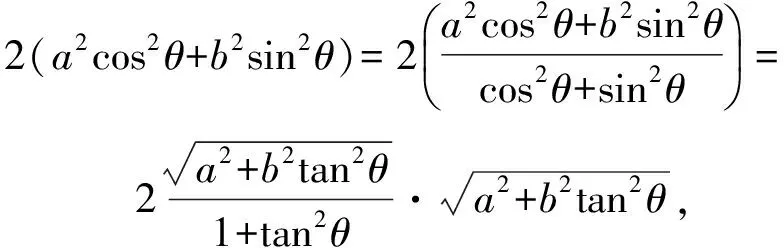
3 “5+4+2”解题算式的教学建议

3.1 树立信心,坚持不懈

据上述阐释和分析可见，认真完成并达到解题算式的要求并非易事，在学习初期更是如此.因此，实施解题算式教学的首要问题是帮助学生树立自信，要有随时受阻的预见性和克服困难的决心.同时，无论是读题、书写，还是从多角度看问题，教师都应该坚持让学生尽可能地发挥，直至在学生已有水平上思考完全.这个过程是漫长而困难的，教师和学生切勿操之过急.只有抓住每次锻炼思维的机会，才能将隐形的成效显著地作用于更加灵活且深刻的题目中.

3.2 分级提示,逐步启发

解题算式强调读题即解题的观点，通过反复品题训练学生思维的灵活性和开放性.但不是每个学生都能自己从不同角度读出题设信息，因而教师对学生要有充分的预设和恰当的引导.通过由远及近的分级提示，激活学生已有的知识和方法，丰富学生看问题的角度.

3.3 留足时间,琢磨通透

学生对解题的认识往往停留在求出答案或作出证明上，草草做完一遍后又投入到新的解题任务中去，并不断抱怨题量大、任务重、难度高，甚至在做了大量练习后，不会的题目还是不会，会做的题目因时隔久远也变得模棱两可.

解题算式要求学生对一个问题、甚至一类问题打通吃透，教师要从观念上改变题海战术，盯住一个题目的各个方面反复研究，并将相关联的知识点和方法技巧同步研究.这需要教师留出足够的时间让学生思考，通过解一个题目，达到会一类题目的效果.

3.4 交流解法,博采众长

“5+4+2”解题算式强调从不同视角出发，选择不同的解题策略，因此每个题目在不同层面上都会有不同的处理方法.不管学生是解题方法的不同，还是具体演算方法的不同，甚至是典型的错误，教师都应鼓励学生相互交流.这不仅可以提高学生解题的自信心，预防可能出现的错误，而且有利于拓展学生的视野,丰富学生的思维,激发学生深入探究的欲望和情绪,营造一个良好的学习氛围.

4 结束语

不可否认，“5+4+2”解题算式是一个包含了不同角度看问题的视角、慢读细品的琢磨、不同策略的选择、以及自编题目再创造多方面的过程.这对教师的教学提出了更多的挑战，也对学生的解题提出了全新的要求.因而在教学相长的动态学习过程中，教师应该不断加强自身的教学水平和解题能力，用包容和学习的心态接受学生的“奇思异想”，充分尊重和鼓励学生的认识，并适时给予修正和改进.