稳中有变 亮点纷呈——2011年数学高考解析几何试题评析

●

(柯桥中学 浙江绍兴 312030)

稳中有变亮点纷呈
——2011年数学高考解析几何试题评析

●张惠民

(柯桥中学 浙江绍兴 312030)

1 教学要求与考查要求

解析几何是高中数学的主干内容，其核心是用代数的方法研究解决几何问题，体现数形结合的思想方法.这类试题主要考查运算求解能力和推理思辨能力.题型一般为一个选择题、一个填空题、一个解答题，分值在20分左右.

2 命题特点和知识类型

2011年的数学高考试题有3个比较明显的特点：一是直线与双曲线的位置关系继续淡化；二是对设参、消参的考查进一步强化；三是探究在什么条件下使某个对象为定值的双向探究问题有明显降温趋势.选择题和填空题以考查基本知识和基本技能为主，但稳中有变，例如，浙江省数学高考理科试题第17题是一个小巧灵活的好题.解答题通常集中在直线和圆、椭圆及抛物线的位置关系方面命制，第(2)小题大多以轨迹问题、最值问题、存在性问题、定值问题、参数求解的形式出现.

3 亮点扫描

亮点1情理之中 意料之外

(2011年江西省数学高考理科试题)

解由已知得

整理得

又

2式比较得

从而

因此

(2011年浙江省数学高考理科试题)

设A(x1,y1)，C(x2,y2),则直线AC的方程为

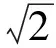
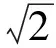
y1=-5y2，

从而

式(1)2÷式(2),得

利用韦达定理可得

解得

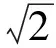
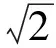
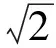
设点A的极角为θ，则点C的极角为π+θ.因为ρA=5ρC，所以

解法3设A(x1,y1)，B(x2,y2),由椭圆定义知

所以

由椭圆第二定义知

从而

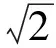
(3)

由式(3),式(4)解得x1=0，所以点A的坐标为(0,±1).

亮点22个方程消2个参数成为一道风景线

(2011年江西省数学高考理科试题)

分析由已知得

又

(6)

求离心率常规的方法往往是先得到关于a,b,c的关系式，再消去b然后解得e．

整理得

(2011年安徽省数学高考理科试题)

图1

式(7)×2-式(8)，得点P的轨迹方程为

2x-y-1=0.

亮点3结论即证即用,考查思维的灵活性

(2)设线段PQ的中点为M，求|OM|·|PQ|的最大值.

(2011年山东省数学高考理科试题)

(2+3k2)x2+6kmx+3(m2-2)=0.

设点O到直线l的距离为d，则

化简得

3k2+2=2m2,

因此

当直线l的斜率不存在时，易验证

也成立.

(2)因为M为线段PQ的中点，而

2|OM|·|PQ|,

评注借用平面几何中的结论避免了代数运算的复杂性，而结论的即证即用使最值求解的过程得以优化.

(3)假设椭圆C上存在点D(x1,y2)，E(x2,y2)，G(x3,y3)，使得

由第(1)小题知

从而

同理可得

评注已证结论的再一次应用无疑使该题的特色更趋显明，这也成为2011年众多解析几何试题中一道好题.

4 复习建议

4.1 有创意地呈现基础知识和基本技能

2011年重庆市数学高考理科试题第20题第(2)小题中的部分表述为：“是否存在2个定点F1，F2，使得|PF1|+|PF2|为定值.”从表面上看，该小题是一个双向探究题，2个定点和1个定值都需要探究，但其本质实为求椭圆的方程.高考复习不该是基础知识和基本技能的简单多次重现，有创意地呈现基础知识和基本技能，无疑有助于激发学生的学习兴趣、提高复习效率.2011年浙江省数学高考理科试题第21题，其中关健性的一步是得到k1,k2是方程

的2个根，若由此适时提出“同一法”的思想，则能提高学生对此类问题的理解层次和记忆深度.

4.2 重视“点参数”的应用

4.3 重视轨迹求解方法的拓展

设点、列式、代入、化简、检验是轨迹求解的最基本方法.例如,2011年陕西省数学高考理科试题第17题、2011年广东省数学高考理科试题第19题、2011年天津市数学高考理科试题第18题均用到此法.而交轨法、参数法、定义法等在轨迹求解中的应用在现行教材中没有系统讲述，需要拓展补充.如2011年安徽省数学高考理科试题第21题主要考查的就是用参数法求轨迹,且有相当的难度.

4.4 提高字母演算的准确性

解析几何中培养学生的思维能力固然重要，但是繁杂、冗长的字母演算是学好解析几何的基础和必备功课.