“亚黄金椭圆”的若干性质

●

(秦安县第二中学 甘肃天水 741600)

“亚黄金椭圆”的若干性质

●罗文军

(秦安县第二中学 甘肃天水 741600)

0 引言

黄金椭圆中有许多美好的性质.同样地，亚黄金椭圆也有许多美好的性质.本文通过对亚黄金椭圆的部分性质作一些探讨，以期达到对圆锥曲线中更多的特殊性质进一步地挖掘和探索，同时对中学生更深入地学习圆锥曲线起引导作用.

为了探讨亚黄金椭圆性质的需要，这里对这个特殊椭圆的一些概念作些说明.

1 亚黄金椭圆的定义

2 亚黄金椭圆性质的探究

性质1在亚黄金椭圆中，2条互为共轭直径所在直线的斜率(斜率存在)之积为-e2.

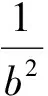
得

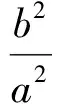
因为在亚黄金椭圆中c2=ab,所以

c4=a2b2,

从而

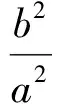
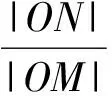
证明设P(x0,y0),则|OM|=|x0|,对b2x2+a2y2=a2b2的2边关于x求导，得

2b2x+2a2yy′=0,

从而

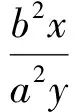
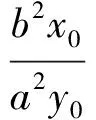
于是

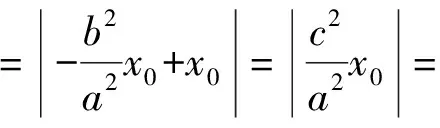
得

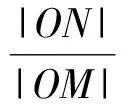
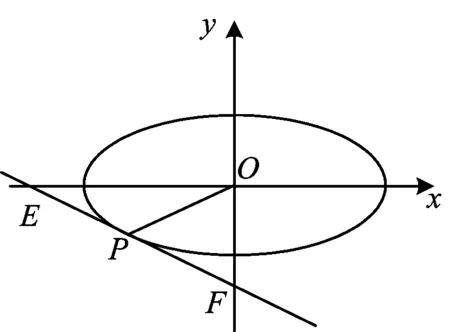
图1

性质3不平行于亚黄金椭圆对称轴的切线斜率与经过该切点和中心的直线斜率之积为-e4.

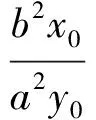
从而

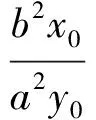
因此

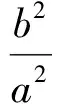
图2

性质4不平行于亚黄金椭圆对称轴且不经过椭圆中心的弦所在直线的斜率与经过该弦中点和椭圆中心的直线斜率之积为-e4.

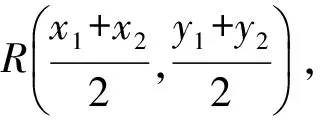
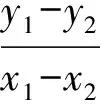
因此

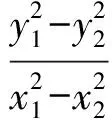
(1)

将式(2)，式(3)代入式(1)，得

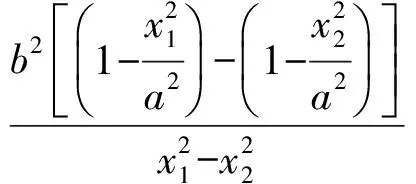
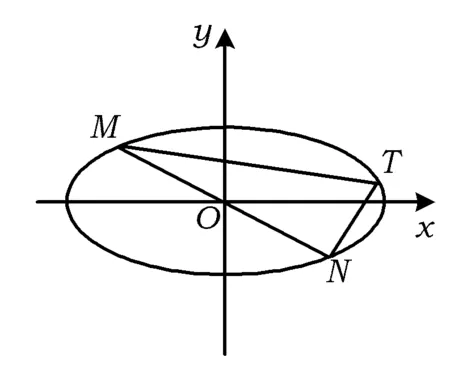
图3

性质5如图3，MN是经过亚黄金椭圆中心的弦，T是亚黄金椭圆上任意一点(顶点除外)，若TM,TN的斜率都存在且不为0，则kTM·kTN=-e4.

证明设M(x0,y0),任意一点T(x′,y′),则N(-x0,-y0).由题意得

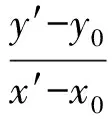
因此

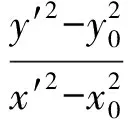
(4)

因为T,M是亚黄金椭圆上的点，所以

将式(5)，式(6)代入式(4)，得

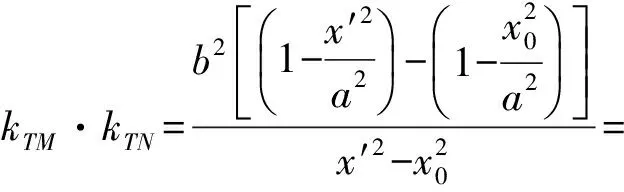
有关亚黄金椭圆的性质远远不止这些，更多性质有待于我们继续去挖掘和探究.

[1] 苏立标.从一道高考试题谈“亚黄金椭圆”的性质[J].数学教学研究，2007(6):39-40.

[2] 陈爱花.“黄金”数列与“黄金”椭圆[J].中学生数学，2006(11):30-31.

[3] 吴文尧.黄金椭圆和黄金双曲线[J].中学教研(数学)，2004(11):27-28.

[4] 魏海涛.椭圆族中的奇葩——黄金椭圆[J].数学教学研究，2008,27(4):35-37.

[5] 阿家斌.优美椭圆(双曲线)的一组性质[J].中学数学教学参考，1997(7):42-43.

[6] 吕林根，许子道.解析几何[M].北京：高等教育出版社，1987.