认识椭圆上的4个特殊点
2011-11-28
●
(杨浦区彰武路同济新村224号甲 上海 200092)
认识椭圆上的4个特殊点
●姜坤崇
(杨浦区彰武路同济新村224号甲 上海 200092)


图1
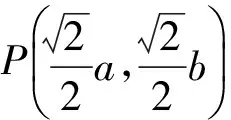
(1)S△PAB=S△PCD;
(2)|PA|·|PB|=|PC|·|PD|;
(3)∠APB=∠CPD.


(2)由题意可得
|PA|2·|PB|2=

同理可得

于是
|PA|2·|PB|2=|PC|2·|PD|2,
得
|PA|·|PB|=|PC|·|PD|.
(3)由第(1),(2)小题的结论知
S△PAB=S△PCD,|PA|·|PB|=|PC|·|PD|.
又


得
sin∠APB=sin∠CPD,
从而
∠APB=∠CPD.

S△PEF=S△ACE+S△BDF.


又

得
S=S△PCD.
两边同减去梯形EFDC的面积即得
S△PEF=S△ACE+S△BDF.

图2

图3



又

于是
|PF1|·|PF2|=|PO|2,
即|PF1|,|PO|,|PF2|成等比数列.
性质4如图4,A是椭圆E在第一象限的一段弧上的动点,A在x轴、y轴上的射影分别为P,Q,则当点A运动到点P的位置时,矩形OPAQ(O为中心)的面积最大.
证明设A(x0,y0)(x0>0,y0>0),矩形OPAQ的面积为S,则

由基本不等式得



图4

图5
性质5如图5,点A是椭圆E在第一象限的一段弧上的一点,B(a,0),C(0,b)是E的2个顶点,则当A在点P的位置时,四边形OBAC(O为中心)的面积最大.
证明设A(x0,y0)(x0>0,y0>0),四边形OBAC的面积为S,则
连结AO,则




性质6如图6,设A(a,0),B(0,b)是椭圆E的2个顶点,E在P处的切线l与x轴、y轴的交点分别为C,D,则AB∥CD,|PC|=|PD|.

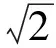
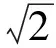
AB∥CD.


图6

图7
性质7如图7,A是椭圆E在第一象限的一段弧上的一点,椭圆E在点A处的切线l和x轴、y轴的交点分别为B,C,则当点A在点P的位置时,△BOC(O为中心)的面积最小.
证明设A(x0,y0)(x0>0,y0>0),△BOC的面积为S,则
切线l的方程为


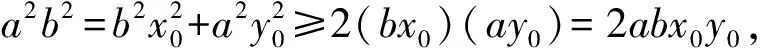
当且仅当bx0=ay0时等号成立,从而

于是


