利用“方差”解竞赛题

●

(枣庄市第十八中学 山东枣庄 277200)

利用“方差”解竞赛题

●李耀文

(枣庄市第十八中学 山东枣庄 277200)

方差公式在解数学题中有着极其广泛的应用.但是有时也会造成一种错觉，好像方差公式仅仅是在统计初步内容中才使用.实则不然，下面笔者就方差公式在解竞赛题中的用武之地举例如下，供赏析参考.

1 方差公式

显然，s2≥0，当且仅当x1=x2=…=xn时，s2=0.

2 应用举例

2.1 求代数式的值

例1已知实数x,y,z满足x+y=5及z2=xy+y-9，则x+2y+3z=________.

(2002年山东省初中数学竞赛试题)

解由x+y=5,可得

x2+y2=25-2xy.

又

z2=xy+y-9,

因此

xy=z2-y+9,

则x+y-1=4,x2+(y-1)2=8-2z2.

视x,y-1为一组数据，则由方差公式得

由s2≥0，知-z2≥0，于是z=0，即s2=0.从而x=y-1，解得

x=2，y=3，

所以

x+2y+3z=8.

例2已知实数x,y,z满足x=6-3y和x+3y-2xy+2z2=0，求x2y+z的值.

(1998年上海市“鹏欣杯”初中数学竞赛试题)

解由x=6-3y,可得x+3y=6,因此

于是

x2+(3y)2=36-6xy=18-6z2.

视x,3y为一组数据，则由方差公式，得

由s2≥0，知z=0，即s2=0.从而x=3y，于是x=3,y=1,所以x2y+z=33×1+0=9.

2.2 求取值范围

例3已知实数a,b满足a2+ab+b2=1，且t=ab-a2-b2，那么t的取值范围是________.

(2001年全国初中数学竞赛试题)

(a+b)2=(a2-ab+b2)+3ab=

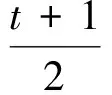
可知

t≥-3.

视a,b为一组数据，则由方差公式得

例4实数a,b,c满足a2-bc-6a+1=0，b2+c2+bc-2a-1=0，求a的取值范围.

(1991年湖北黄冈地区初中数学竞赛试题)

视b,c为一组数据，则由方差公式得

由于s2≥0，因此

3a2-20a+2≤0，

解得

2.3 证明等式或不等式

例5已知实数a,b,c满足a=6-b，c2=ab-9.求证：a=b.

证明由a=6-b，c2=ab-9，知

a2+b2=(a+b)2-2ab=18-2c2.

视a,b为一组数据，则由方差公式得

由s2≥0，可知c=0，即s2=0，所以a=b.

(1991年“曙光杯”初中数学竞赛试题)

证明由a+b=-c得

a2+b2=c2-2ab，

由abc=1得

因此

视a,b为一组数据，则由方差公式得

化简得c3≥4，所以

2.4 解方程

例7已知a,b,c满足方程组

试求方程bx2+cx-a=0的根.

(2001年全国初中数学联赛试题)

因此

a2+b2=(a+b)2-2ab=

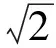
视a,b为一组数据，则由方差公式得

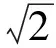
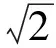
例8解方程:

x=a2,y=b2+1,z=c2+2.

原方程可化为

4(a+b+c)=a2+b2+c2+12，

则

a2+b2+c2=4(a+b+c)-12.

视a,b,c为一组数据，则由方差公式得

由s2≥0，可知a+b+c=6，于是s2=0，从而

a=b=c=2,

所以

x=4,y=5,z=6.

经检验,x=4,y=5,z=6是原方程的根.

2.5 解方程组

例9解方程组：

(2008年广东省广宁市初中数学竞赛试题)

解视x,y,z为一组数据，则由方差公式得

(x-1)2+(y-1)2+(z-1)2=ns2=0,

所以

x-1=0，y-1=0,z-1=0,

从而

x=1,y=1,z=1,

显然它们满足方程组中的3个方程.故原方程组的解为x=1,y=1,z=1.

例10解关于实数的x,y,z方程组：

(2007年山东省泰安市初中数学竞赛试题)

可得

2x+(3y+3)=13-z,

因此

(2x)2+(3y+3)2=104-4z-z2.

视2x,3y+3为一组数据，则由方差公式得

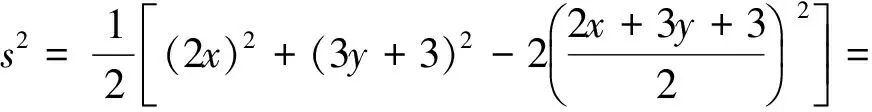
由s2≥0，可知z=4，于是s2=0，从而

2x=3y+3,

所以

x=3,y=1.

故原方程组的实数解为x=3,y=1,z=4.

2.6 求最值

例11已知a,b为实数，且a2+ab+b2=3，若a2-ab+b2的最大值是m，最小值是n，求m+n的值.

(2008年天津市初中数学竞赛初赛试题)

解设a2-ab+b2=t，且a2+ab+b2=3，则

于是

(a+b)2=(a2-ab+b2)+3ab=

解得t≤9.视a,b为一组数据，则由方差公式得

于是t≥1，故1≤t≤9.从而a2-ab+b2的最大值是m=9，最小值是n=1，所以m+n=10.

例12实数x,y,z满足x+y+z=5,xy+yz+zx=3，则z的最大值是________.

(2004年“信利杯”全国初中数学竞赛试题)

解由x+y+z=5，xy+yz+zx=3可得

x+y=5-z,

因此

x2+y2=(x+y)2-2xy=-z2+19.

视x,y为一组数据，则由方差公式得

由s2≥0，可知

3z2-10z-13≤0，

解得

综上所述，利用方差公式解题，其关键是根据题设条件，构造出一组数据，再运用方差公式

建立等式，结合s2≥0,通过运算简化得出s2=0，并借助非负数性质即可解决问题.这种利用方差解题的思路方法，有利于启迪思维、开拓视野、提高综合运用知识的解题能力，应予以重视.