人口普查误差刍议

胡桂华

（广西财经学院 数学与统计系，广西 南宁 530003）

人口普查误差刍议

胡桂华

（广西财经学院 数学与统计系，广西 南宁 530003）

许多国家每次人口普查之后都要对其进行质量评估，计算人口普查误差，包括净误差及其构成部分（普查遗漏和普查错误计数）。通常采用先估计净误差，然后估计普查错误计数和普查遗漏。人口普查误差计算的关键是估计总体实际人口数。目前多数国家是使用基于捕获－再捕获模型和事后分层的双系统估计量估计实际人口数。最近1～2年美国提出使用基于罗吉斯蒂回归模型的双系统估计量估计实际人口数。研究结论表明：真正的人口普查误差其实是不能计算的；基于罗吉斯蒂回归模型的双系统估计量由于不受样本量限制而可以选择较多的事后分层变量，因而它优于基于事后分层的双系统估计量。

人口普查；人口普查误差；人口普查质量评估

一、真正的人口普查误差是不能计算的

向一个目标射击，弹着点与目标之间的距离叫做射击误差。在人口普查中，全国的实际人口数相当于射击的目标，人口普查得到的结果相当于弹着点，人口普查结果与全国实际人口数之差是人口普查误差。

在这里，人口普查误差与射击误差之间有一个重要的区别。射击目标是已知的，因此，射击误差是可以确切计算的。相反，全国实际人口数是未知的，人口普查误差就无法确切地计算出来。

如今，世界各国在每一次人口普查之后都要对本次人口普查工作进行质量评估，其中一件最重要的事情就是要计算本次人口普查的误差。怎样来计算这个误差呢？大家所走的都是这样一条共同的路径：在进行质量评估的时候，与人口普查相独立地另外计算一个全国人口数的估计值，然后用人口普查结果与它相减，用所得之差作为人口普查误差。

那么，怎样得到全国人口数的估计值呢？通常可能会使用的办法分成三类。第一类是利用人口的出生、死亡、迁移及其他行政记录资料推算普查时点的人口数［1］；第二类是用抽样调查的方法进行一次普查时点人口数目的再调查来估计普查时点的人口数；第三类是把行政记录资料（或人口再调查资料）与人口普查资料结合在一起形成双系统资料来估计普查时点的人口数［2］8－9。

于是，人们很自然地会提出这样一个问题：用上面的不论哪一种办法所算出来的人口数果真能够当作全国实际人口数来使用吗？如果它们是全国实际人口数，如果它们比人口普查的结果更可信，那为什么不用它们来取代人口普查数字呢？如果不能认定它们比人口普查的结果更可信，那又凭什么用它们做基准来评判人口普查的误差呢？

其实，人口普查也好，在人口普查之后的质量评估工作中计算人口数估计值也好，都是对全国人口总体这个对象的规模进行观测，这种观测是在做随机试验，观测结果的数值是随机试验的样本值。在人口普查之后进行质量评估计算人口数估计值事实上与人口普查结果具有相同的统计意义，并不能把它当作评价人口普查误差的基准。两个数字之差其实并不是人口普查误差。那么，这个差数究竟是什么呢？

现在假定，我们在一组不变的条件下对某一个固定时点上全国人口总体的规模进行了两次独立重复观测，前一次观测是人口普查，结果记做X1，后一次观测是在人口普查质量评估工作中进行了一次“再普查”，结果记做X2。显然，X1和X2是同一个随机变量X的样本值。样本平均数记做珡X。我们用样本平均差来描述随机变量X的散布情况，即：

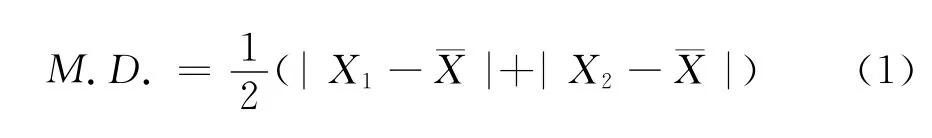
只要对式（1）进行脱去绝对值符号后简单的代数运算便可得到式（2）：

这就是说，X1与X2之差的绝对值实际上是用以描述随机变量X散布情况的样本平均差，而观测值结果的散布特征数表明了观测的精度，散布特征数的数值越小表明观测值的散布越集中，表明观测的精度越高，也就是表明人口普查的工作质量越好。注意，在这里说的是工作质量，而不是人口普查计算出来的人口数目这个数字的质量。

再说一遍，X1与X2之差的绝对值的大小，并不是表明X1距离实际人口数目的远近，而只是表明了人口普查的整体工作水平。

在实际工作中，人口普查与人口普查质量评估调查不可能在不变的条件下独立重复进行，因此，人口普查结果与质量评估结果之差也不是上述严格上的人口普查随机试验的平均差。但是，不管怎么说，我们在逻辑上把它看作评价人口普查工作质量的一个统计量还是合理的。

现在我们知道人口普查误差其实是不能计算的，人们在评估人口普查质量时计算出来的人口普查误差，其实仅仅是评价人口普查工作质量的一个统计量，它并不能说明在人口普查中所计算出来人口数字距离实际人口数的远近。不过，由于世界各国都约定俗成地一直把这个统计量叫做人口普查误差，所以，我们只要在心里知道它的实际意义就足够了，至于在名称上，不妨继续把它叫做人口普查误差，没有必要加以改变。当然，如果在质量评估工作中计算了一个当之无愧的实际人口数估计值的话，则我们可以把人口普查结果与这个估计值的差叫做人口普查误差的估计量。那么，怎样才够称得上是当之无愧的实际人口数估计值呢？大数法则告诉我们，如果对人口规模进行无限多次独立重复观测的话，那末，观测结果的平均值会向人口规模的实际值逼近。对于有限次的观测，用观测结果的平均值估计实际人口数的有效性取决于样本量（观测次数）。照此看来，如果用质量评估调查资料与人口普查资料结合在一起形成双系统资料来估计实际人口数，似乎可以认为它算是实际人口数的估计值，只不过很勉强——样本量太小了（仅仅为2）。

二、用双系统资料估计实际人口数

人口普查质量评估工作中一件重要的事情是估计实际人口数。把质量评估时所收集的人口数目资料与人口普查资料这两个资料系统结合在一起来构造估计量，可以充分地把普查和质量评估调查的信息尽可能充分地利用起来，有利于提高估计量的精度。所以，在人口普查质量评估中采用双系统估计技术是目前世界各国较为流行的做法。

双系统估计量源于统计学中著名的“捕获－再捕获”模型［3］。这个模型的典型问题是：一个封闭的鱼塘中有若干条鱼，它们具有相同的不为0的被捕到的概率。想要知道池中鱼的数目。为此，先从池中捕获E条鱼，在它们每一条的身上做上记号，然后放回池中。待池中的鱼充分混匀后，再从池中与前一次相独立地捕获P条鱼，清查其中涂有记号的鱼的数目，结果为M条。于是，池中鱼的数目N的估计量为

在统计学文献中，上述结果是通过求解多项分布的未知参数推出的。事实上，通过两次相互独立的捕获形成了一个2行2列四格表，它的四个组格分别是：两次都被捕到、第一次被捕到而第二次未被捕到、第二次被捕到而第一次未被捕到、两次都未被捕到。各组格中鱼的数目相当于N次投球试验中各组格落入球的次数，它们服从多项分布，参数是四个组格各自的进球概率以及试验次数N。根据样本所提供的前三个组格中鱼的数目以及两次捕获相互独立的设计安排，四个组格各自的进球概率可以被估计，这样便可以列出根据样本信息求解多项分布未知参数N的方程式，所得到的解便是式（3）。

在人口普查及其质量评估中，把人口普查的正确计数结果记做E，把质量评估中对普查时点人数的追溯性再普查正确计数结果记做P，把同时出现在人口普查正确计数人名单和再普查正确计数人名单中的人员人数（称做匹配人数）记做M，套用式（3），得到普查时点人口总体实际人口数的双系统估计量＾N。在这里，所谓对人口的正确计数人数，是指属于目标人口总体的成员并且个人信息填写完全并在正确的地点计数的人数，它是从人口普查登记名单人数中剔除掉其中的错误登记人数、个人信息填写完全但在错误地点计数的人数、个人信息填写不完全不过尚能符合普查数据定义者的人数、个人信息填写不完全以致无法符合普查数据定义者的人数这样四种情况的人数［4］。其中的错误登记人数与另外三种情况不同，另外三种情况都和正确计数人数一样是对属于目标人口总体的成员的计数，而错误登记人数是对不属于目标人口总体成员的计数。错误登记指的是下面的一些登记：普查时点以后出生的人、虚构的人（把宠物错当成了人）、重复的登记和由于没有填写姓名或是仅仅填写了姓名而漏填了其他的所有统计特征因而无法确认这个登记究竟是谁，等等。

上面说的E、P、M，都是指人口有限总体的总体值，然而，人口普查质量评估调查是从人口有限总体中抽取概率样本来进行的。例如，从总体中以普查小区为抽样单位抽取了一个样本。这时为了应用基于“捕获－再捕获”模型的双系统估计量式（3），应该进行如下的操作：首先，分别在样本的各个普查小区中逐一访问住房单元，追溯登记普查日该住房单元中的居民（如果当时的居民此时已经迁出本小区则由邻居帮助追溯），形成小区的普查登记人口名单；其次，分别在样本的各个普查小区中对人口普查登记的人口名单进行审查，剔除其中的错误登记（此项工作实际上是与下面一项工作合在一起进行的）；再次，分别在样本的各个普查小区中用质量评估调查人口名单与普查登记人口名单进行比对，找出二者之间的重叠部分（匹配部分）。这样，我们就在样本的各个普查小区（各个i小区）得到了观察值Ei、Pi、Mi。用样本观察值分别构造总体的E、P、M的估计量、、，用这三个估计量替换式（3）中的三个总体值，写出式（3）的下列估计量为：

这里要说明一个重要的问题。“捕获－再捕获”模型要求池塘中的鱼具有相同的不为0的被捕到的概率。但是在人口中，性别、年龄、民族、居住地类型等变量都会影响被登记概率。因此，在构造人口数目的双系统估计量时，应当首先对全国人口按性别、年龄、民族、居住地类型等等这些影响被登记概率的标志进行交叉分组（分组也称为分层），把被登记概率相同的人放在同一个组内，把被登记概率不同的人放入不同的组，在此基础上，分别在各个组中构造双系统估计量。在实际工作中，此种分组（分层）的操作只能待样本抽取出来以后在样本中进行，抽样调查理论中把它叫做抽样后分层［5］。于是式（4）应当分别在各个事后层内应用。事实上，只要是分别在样本的各个事后层中构造估计量，就相当于对总体进行了分层，所构造的估计量分别就是总体各个层的估计量。在实际操作中，抽样后分层是在样本的各个普查小区中进行的，就是把i小区的质量评估调查人口名单和普查登记人口名单按照选定的性别、年龄、民族、居住地类型等标志进行交叉分层，然后分别在各个交叉层内进行两个名单的匹配性比对，分别得到各个交叉层的观察值Eiv、Piv、Miv（下标v表示某一个交叉层）。用v层的样本观察值构造v层的E v、Pv、M v的估计量用这三个估计量计算式（4）得到。显然，把全国所有v层的相加便得到全国的

有的国家在构造双系统估计量时省去了抽样后分层这个环节［6］。他们认为，在一个范围很小的区域中，可以近似地认为其中的居民被登记概率大致相同，因此可以在这样的区域中直接计算双系统估计量。这显然是不符合实际的，例如，即使是住在同一个居民楼中的居民，他们在人口普查中被登记的概率也不相同。有的国家在样本小区不进行抽样后分层而直接构造双系统估计量，然后将其一级一级地向上推，最后在全国这一级构造一个校正系数来校正由于背离等概率要求所带来的偏差。但是，并没有足够的证据来证明这个系数能够完成校正偏差的任务。

在上面的叙述中，质量评估调查这一资料系统所使用的是在质量评估工作中重新进行一次追溯性现场调查得到的资料。在应用双系统估计量的国家中，多数属于这种情况。除此以外，也有的国家由于拥有较健全的人口登记行政记录（例如人口登记册），因而用人口登记行政记录资料作为质量评估调查资料系统，将其与人口普查资料系统结合在一起来构造双系统估计量。首先对每个样本普查小区中的人口登记行政记录资料进行审查，确认这个资料在人口普查时点的状态，剔除其中的错误登记，然后进行抽样后分层并进行与普查登记人口名单的匹配性比对，在此基础上获得样本观察值并构造所需要的各种估计量。

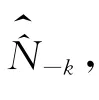
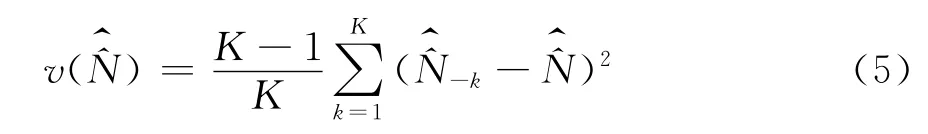
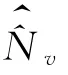
三、把罗吉斯蒂回归模型应用于双系统资料来估计实际人口数

抽样后分层方法在实际应用中有明显的局限性。对于一个固定的总样本量来说，交叉分层所用的分层标志越多，各个交叉层所分配到的样本量就会越少，如果分层标志选得太多，有可能会出现有的事后层样本量过少甚至没有样本单位的情况，这就限制了分层标志的使用，以致一些重要的标志不得不被舍弃。针对这个缺点，统计学家们设计了用罗吉斯蒂回归模型来实现事后分层目标的方法，即把我们选择的事后分层标志全部设置为罗吉斯蒂回归模型的自变量，该多元自变量的一个值等同于这些变量交叉分层体系下的一个组格（一个事后层）。罗吉斯蒂回归方法与直接进行抽样后分层相比有两个优点：一是它可以不受样本量的限制选择较多的变量，二是它可以直接使用连续型变量（而不必要将其降级为分类变量）［9－10］。

用罗吉斯蒂回归模型估计实际人口数的路径是：用普查登记人口名单资料系统建立一个罗吉斯蒂回归模型，求得该资料系统中的每个人在普查中正确计数概率的模型预测值。再用质量评估调查人口名单资料系统建立一个罗吉斯蒂回归模型，求得该资料系统中的每个人与普查名单匹配概率的模型预测值。将同一个人的前者与后者相比，在普查登记人口名单范围内将各人的这个比值求和，得到实际人口数的估计量。

按照罗吉斯蒂回归模型的定义，模型的因变量应当采集全国普查登记人口名单中每个人的普查中正确计数概率和全国质量评估调查人口名单（假若有这个名单的话）中每个人的与普查名单匹配概率。测度一个人该概率值的途径是在全国普查登记人口名单中形成一个由一些与该人条件完全相同的人组成的规模足够大的群体，在这个群体中计算正确计数频率（同样计算匹配频率）。所谓“条件完全相同”指的是影响正确计数概率（匹配概率）的各种决定因素的表现相同。这些决定因素是什么呢？显然，它们应该是罗吉斯蒂回归模型所选择的全部自变量。于是，这就要求我们用这些自变量对人口总体进行交叉分层，在所形成的交叉层内计算正确计数频率（匹配频率）。但是，现在我们不方便进行此种操作。原因是如果可以进行此种操作的话，那就又回到了前面所介绍的抽样后分层的做法，那就不需要使用罗吉斯蒂回归模型了。面对这个难题，统计学家们设计了一种“退让一步”的方案，就是选择另外的分层标志，使得正确计数概率（匹配概率）决定性因素的各种表现大致相同的人进入同一层，在这样的层中计算正确计数频率（匹配频率）。例如，美国2010年人口普查质量评估调查中，在进行质量评估调查人口名单与普查登记人口名单的比对之前先进行了两个调查中编制的住房单元地址目录的初始比对，初始比对的结果被划分为7种情况：1＝匹配但需要后续调查；2＝可能匹配；3＝家庭中有一部分人没有匹配需要后续调查；4＝整个家庭没有匹配需要后续调查，家庭名称不重复；5＝不匹配，来自名称重复的家庭；6＝在后续调查之前状态已能确定；7＝用于进行比对的信息不足。住房单元连同住在里面的居民便被划分为这样7个层，美国方案中将其称之为“集区”（cell）。初步认为，进入同一个“集区”的人，影响他们正确计数概率（匹配概率）的各种决定性条件的取值是大致相同的。于是，方案规定在各个“集区”中计算正确计数频率（匹配频率）。

于是，现在就可以得到全国普查登记人口名单中每个人的普查中正确计数概率估计值，对它们进行罗吉斯蒂变换以后得到每个人普查中正确计数概率估计值的罗吉斯蒂变换值，将这些罗吉斯蒂变换值与每个人的回归模型自变量取值结合在一起，依照罗吉斯蒂回归模型的估计规则，用加权最小平方法完成参数估计，得到普查正确计数概率罗吉斯蒂回归模型估计式。把全国普查登记人口名单中一个人的回归模型自变量取值代入模型估计式，得到这个人普查正确计数概率的模型预测值（它是该人在普查中正确计数概率的数学期望值）。依照同样的过程，可以建立质量评估调查匹配概率罗吉斯蒂回归模型估计式并通过它得到质量评估调查人口名单中每个人的匹配概率的模型预测值。将同一个人的普查正确计数概率的模型预测值除以匹配概率的模型预测值，在普查登记人口名单范围内将各人的这个比值求和，得到实际人口数的估计量。

可以证明，如果上面计算计数概率和匹配概率估计值所用的“集区”是用罗吉斯蒂回归模型自变量作为分层标志形成的，那么，用上述方法构造的实际人口数的估计量等价于在每个这样的“集区”中用式（3）构造“集区”实际人口数双系统估计量，再将所有“集区”的估计量合成以后的结果。可见，用罗吉斯蒂回归模型所构造的实际人口数估计量与用罗吉斯蒂回归模型自变量分层基础上构造的实际人口数“捕获－再捕获”模型双系统估计量的接近程度，取决于我们划分“集区”实际所采用的分层标志——实际采用的分层标志越接近于罗吉斯蒂回归模型自变量，用罗吉斯蒂回归模型所构造的实际人口数估计量就越接近于“捕获－再捕获”模型双系统估计量。

在实际应用中，建立罗吉斯蒂回归模型估计式所依据的样本并不是全国人口，而是从全国以普查小区为单位抽取出来的有限总体概率样本。这就要求，在“集区”中，先要用其中的有限总体概率样本来构造全国人口有限总体样本“集区”的正确计数频率和匹配频率的估计量。另外，在用加权最小平均方法估计模型参数的时候，也要考虑到所使用的数据仅仅是有限总体概率样本的资料，需要进一步应用有限总体概率抽样理论的有关规则把这些数据“膨胀”到全国有限总体。

前面说过，负责任地提供估计量的精度是统计工作的“行规”。用罗吉斯蒂回归模型所构造的实际人口数估计量的方差也如“捕获－再捕获”模型双系统估计量的方差一样，用“刀切法”来估计。

四、对人口普查遗漏人数和错误计数人数的估计

评估人口普查工作的质量，除了希望了解人口普查误差之外，还希望了解被人口普查遗漏的人数以及在人口普查中错误计数的人数［11］。这是因为，第一，人口普查误差是遗漏人数与错误计数人数相抵的结果（下面即将讲到），这二者的数值越接近，算出来的人口普查误差数值越小，因此，只观察人口普查误差会低估人口普查工作中存在的问题；第二，遗漏人数和错误计数人数分别来源于人口普查工作的不同缺陷，分别观察这两种错误，才便于有针对性地改进人口普查工作。

人口普查误差、遗漏人数、错误计数人数之间的关系由式（6）表示：

人口普查误差＝普查登记人数－目标人口总体实际人口数＝（正确计数人数＋个人信息填写完全但在错误地点计数人数＋个人信息填写不完全但尚能符合普查数据定义者的人数＋个人信息填写不完全以致无法符合普查数据定义的人数＋错误计数人数）－（正确计数人数＋个人信息填写完全但在错误地点计数人数＋个人信息填写不完全但尚能符合普查数据定义者的人数＋个人信息填写不完全以致无法符合普查数据定义的人数＋遗漏人数）＝错误计数人数－遗漏人数 （6）

由式（6）可看出，在遗漏人数和错误计数人数这二者当中，只要设法算出其中之一，再联系已算出的人口普查误差，便可推出另外一个。

首先，直接估计错误计数人数（间接推算遗漏人数）。由式（6）中普查登记人数的几个组成部分可以写出：

错误计数人数＝普查登记人数－正确计数人数－个人信息填写完全但在错误地点计数人数－个人信息填写不完全但尚能符合普查数据定义者的人数－个人信息填写不完全以致无法符合普查数据定义的人数 （7）

可见，只要在人口普查登记表以及质量评估调查登记表中设置必要的调查项目，使我们有可能用质量评估调查中抽取出来的普查小区样本来构造式（7）等号右边第二、三、四、五项的估计量，错误计数人数便可得到估计。关于估计量的构造方法以及估计量的方差的计算方法，这里略去不做介绍。

其次，直接估计遗漏人数（间接推算错误计数人数）。本方法是基于下面的平衡关系式来构建设计思路的，即：

本次普查遗漏人数＝上次普查登记人数＋上次普查遗漏人数＋上次普查后至本次普查前增加的人数－上次普查后至本次普查前减少的人数－本次普查登记人数 （8）

如果一个国家每间隔10年搞一次人口普查，式（8）中的“上次普查”指的是10年前的那一次人口普查。根据这个关系式对操作方法所做的设计是：把上次普查登记的人口名单作为第一个抽样框，把上次普查的质量评估调查中从当时所抽取的样本中查找出来的上次普查登记遗漏的人口名单作为第二个抽样框，把上次普查后至本次普查前出生人口名单以及从国外向本国移民人口名单做为第三个抽样框。分别从这三个抽样框中以人为抽样单位抽取样本。对样本中的每个人，清查其是否已经死亡或者是否已经移民到国外。然后对样本中余下的确认其仍为本次人口普查时点上的本国人口的那些人，到本次人口普查登记的人口名单中查找匹配者，其中未能找到匹配者的那些人便是被本次普查遗漏的人。当然，根据这个遗漏人名单算出的遗漏人数是仅仅局限在样本范围的人数，在设计中还安排了用抽样权数对样本数据进行加权，从而将样本数据“膨胀”到总体的程序。另外还设计了计算估计量的方差的程序。

该方法的设计中，有三个问题值得进一步讨论。第一，由式（8）给出的平衡关系，对一个地区（全国、一个省、样本中的一个普查小区）的总体值来说是成立的，现在是分别对各个相加项建立抽样框分别抽取样本分别构造各个加项的估计量，这时由于存在抽样误差，会导致平衡关系被破坏。因而，这时的“本次普查遗漏人数”估计量中，除了自身的抽样误差以外，还包含了平衡关系被破坏所形成的误差。第二，构造“本次普查遗漏人数”估计量的方法是，分别用来自各个抽样框的样本中“被本次普查遗漏的人数在样本量中所占比例”这个统计量乘以本抽样框的人数这一总体值，得到本抽样框的本次普查遗漏人数总体值。对于所采用的方法应注意，“上次普查登记遗漏的人口名单”并不是总体的名单，而仅仅是上次普查质量评估中从样本得到的名单，用这个名单直接点数得到的人数并不是一个总体值。所以，在应用上述路径的时候，需要把这个名单的人数放大成总体值。相应地，在计算估计量的方差的时候，要把这个估计过程的方差考虑在内。第三，上次普查中的错误计数者，我们只有它的总体人数的估计量，并没有全国所有错误计数者的名单。所以，现在从“上次普查登记的人口名单”这个抽样框中抽取的样本中会包含错误计数者而无法将其识别出来。在本次普查登记人口名单中是不会有这些人的，于是，它们会被误认作普查遗漏人数加以计算。

［1］ Siegel J S.Estimates of Coverage of the Population by Sex，Race，and Age in the 1970 Census［J］.Demography，1974（11）.

［2］ Robert M，Bell，Michael.Coverage Measurement in the 2010 Census［M］.Washington，D.C.：the National Academies Press，2008.

［3］ Le Cren E D.A Note on the History of Mark－recapture Population Estimates［J］.J.Animal Ecol，1965（34）.

［4］ Mary H Mulry，Donna K，Kostanich.Framework for Census Coverage Error Components［J］.ASA Section on Survey Research Methods，2006（8）.

［5］ U.S.Bureau of the Census.Accuracy and Coverage Evaluatio of Census 2000：Design and Methodology［R］.U.S.Census Bureau，2004.

［6］ Uganda Bureau of Statistics.Post－enumeration Survey：2002 Uganda Population and House Census［R］.Uganda Bureau of Statistics，2005.

［7］ Yvonne M M，Bilfhop.离散多元分析：理论与实践［M］.张尧庭，译.北京：中国统计出版社，2000.

［8］ Anne Renand.Coverage Estimation for the Swiss Population Census 2000：Estimation Methodology and Results［R］.Swiss Federal Statistical office.2004.

［9］ Richard Griffin，Thomas Mule，Douglas Olson.2010 Census Coverage Measurement：Initial Results of Net Error Empirical Research using Logistic Regression［J］.American Statistical Association，2006（8）.

［10］Vincent Thomas Mule，Jr Donald Malec，Jerry Maples.Using Continuous Variables as Modeling Covariates for Net Coverage Estimation［J］.U.S.Bureau Census on Section Survey Research Methods，2008（8）.

［11］Vincent Thomas Mule，Donald Malec，Lynn Imel，Nganha Nguyen，Michael Modoff.Missing Data Methods For the CCM Component Error Estimation［J］.Secton on Suvey Recsench Methods－JSM，2009（8）.

Informal Discussion on Population Census Error

HU Gui-hua

（Mathematics and Statistics Department，Guangxi University of Finance and Economics，Nanning 530003，China）

Many countries carry out its quality evaluation after each population census with calculating population census error，including net error and its component（census omissions and erroneous inclusions）.Net error is usually estimated firstly and then its census omissions and erroneous inclusions.This article studies how to treat and calculate census error.The key of census error calculation is to estimate the overall actual population.At present most countries use dual system estimator based on capture－recapture model and post－stratification to estimate total actual population.Recent 1－2 years the United States put forward to use dual system estimator based on logistic regression model to estimate actual population.Research conclusions show：The real census error calculation is actually impossible；dual system estimator based on logistic regression model is not limited by sample size and may choose more post－stratification variables，so it is better than the dual system estimator based on post－stratification.

population census；population census error；population census quality evaluation

（责任编辑：李 勤）

C829.1

A

1007－3116（2011）11－0012－07

2011－06－22

国家社会科学基金项目《我国人口普查质量评估方法研究》（10XTJ003）；全国统计科学重大项目《行政记录在人口与就业统计中的应用》（2009LD003）

胡桂华，男，湖北武汉人，经济学博士，教授，研究方向：统计调查与数据处理。

book=18,ebook=120

【统计应用研究】