使用变异系数和Kurtosis系数的双辅助变量的比估计

卢静莉

（内蒙古工业大学 理学院，呼和浩特 010051）

0 引言

在抽样调查中，辅助信息常常被用来提高估计量的精度，当有多个辅助信息可以利用时，估计量的精度会大幅度提高，如何利用多个辅助信息来提高估计的精度成为人们研究的热点[1～3]。本文拟定义一种使用变异系数和kurtosis系数的双辅助变量的比估计法，研究这种方法下估计量的均方误差，证明在一定条件下这种方法下的估计量优于传统的使用双辅助信息的比估计量，同时对这些估计量进行比较。

1 已有的一些比估计量

1.1 Sisodia and Dwivedi单辅助变量比估计量[4]

设Y是调查指标，X是辅助信息，当辅助变量X的变异系数Cx已知时，Sisodia and Dwivedi定义的比估计量为

1.2 Upadhyaya and Singh单辅助变量比估计量[5]

当辅助变量X的变异系数Cx和Kurtosis系数β2(x)已知时，Upadhyaya and Singh定义的比估计量为

均方误差

1.3 传统的双辅助变量比估计量[6]

当有两个辅助信息X1和X2可利用时，定义双辅助信息的比估计量为

均方误差

其中，w1,w2是适当选取的权，w1+w2=1；Cy,Cx1和Cx2分别是Y,X1和X2的变异系数；ρyx1,ρyx2,ρx1x2分别是Y与X1，Y与X2，X1与X2的相关系数。

2 使用变异系数和Kurtosis系数的双辅助变量的比估计

定义1 Y是调查指标，X1,X2是辅助信息，w11,w12,w21,w22,w31,w32是适当选取的权，w11+w12=1，w21+w22=1，w31+w32=1,则的估计量定义为

则均方误差

3 效率比较

首先，把使用变异系数和Kurtosis系数的双辅助变量的比估计量同传统的双辅助信息比估计量进行比较，得到如下结论：

其次,对使用变异系数和Kurtosis系数的双辅助变量的比估计量的三种估计量进行比较，得到如下结论：

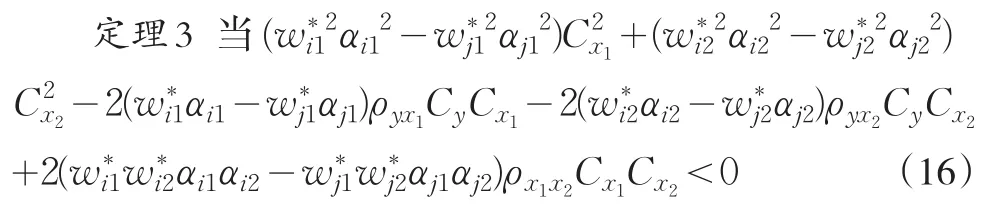
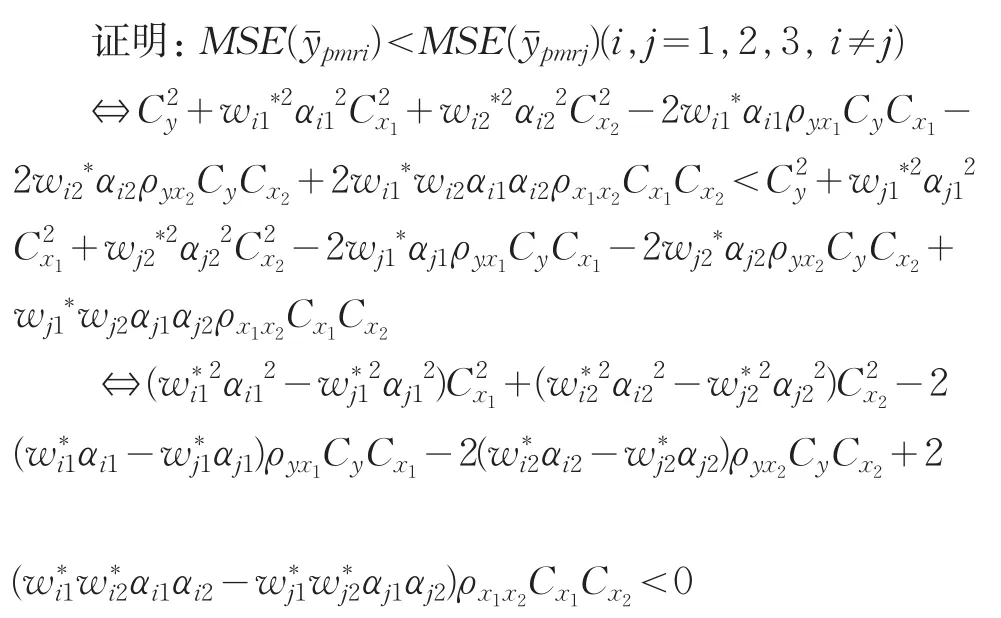
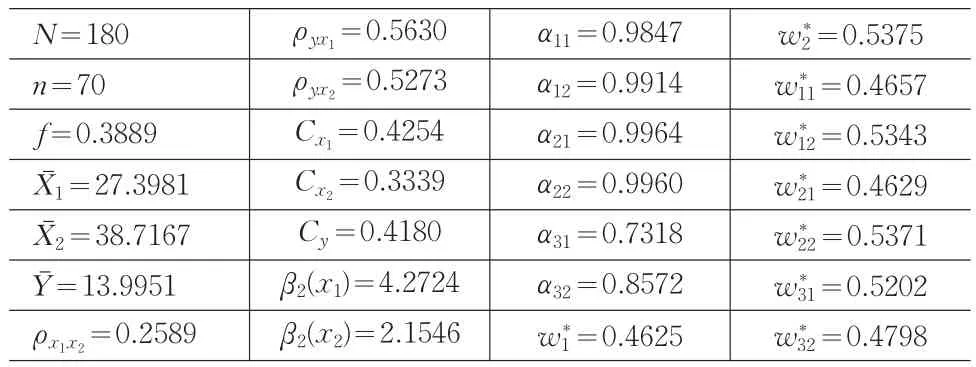
表1 统计数据

4 数值比较

下面以表1中的数据为例来验证定理2和定理3。

表2 比估计量的均方误差

从表2中可以看出第一种定义的比估计量是最优的，这是因为当i=1时(15)式及（16）式都得到了满足

同时从表2还可以看出除了第一种定义的估计量外，第二种定义的估计量也优于传统的双辅助信息比估计量。

5 结论

文本定义了三种使用变异系数和Kurtosis系数的双辅助变量的比估计量，研究了它的均方误差，并且指出均方误差最小时权的取值，证明了当满足一定条件时，新定义的双辅助信息比估计量优于传统的双辅助信息比估计量；同时也得到了这三种估计量一个优于另一个的条件；并且从数值方面得到了验证。

[1]W.A.Abu-Dayyeh,M.S.Ahmed,R.A.Ahmed,et al.Some Estimators of a Finite Population Mean Using Auxiliary Information[J].Applied Mathematics and Computation,2003,(139).

[2]C.Kadilar,H.Cingi.A Study on the Chain Ratio-type Estimator[J].Hacettepe Journal of Mathematics and Statistics,2003,(32).

[3]C.Kadilar,H.Cingi.A New Estimator Using Two Auxiliary Variables[J].Applied Mathematics and Computation,2005,(162).

[4]B.V.S.Sisodia,V.K.Dwivedi.A Modified Ratio Estimator Using Coef⁃ficient of Variation of Auxiliary Variable[J].Journal of Indian Society Agricultural Statistics,1981,(33).

[5]L.N.Upadhyaya,H.P.Singh.Use of Transformed Auxiliary Variable in Estimating the Finite Population Mean[J].Biometrical Journal,1999,41(5).

[6]冯士雍，倪加勋，邹国华.抽样调查理论与方法[M].北京：中国统计出版社，1998.