风险规避情形下第一价格拍卖的非参数估计方法

安 欣，刘树林

（1.北京林业大学 经济管理学院，北京 100083；2.对外经济贸易大学 国际经济贸易学院，北京 100029）

风险规避情形下第一价格拍卖的非参数估计方法

安 欣1，2，刘树林2

（1.北京林业大学 经济管理学院，北京 100083；2.对外经济贸易大学 国际经济贸易学院，北京 100029）

在拍卖实证研究的大量文献中，越来越多的证据表明投标人更趋向于风险规避，然而目前拍卖计量方法通常只考虑风险中性的情形。针对这一问题，推广了针对第一价格拍卖的非参数估计方法，给出了多个风险规避参数估计量来处理风险规避的情形，并总结了相应的估计过程。为验证估计效果，蒙特卡罗模拟实验被用于进行分析和评价。实验结果表明，无论是对风险规避参数，还是私有估值的估计，总体上都能取得不错的效果，验证了方法的有效性，同时为风险规避参数估计量的选择提供了一些指导性建议。

第一价格拍卖；风险规避；非参数估计；蒙特卡罗模拟

一、引 言

拍卖是具有明确交易规则的资产配置方式和价格发现机制之一，在市场经济中得到广泛的应用。自从1956年Friedman发表了第一篇关于拍卖理论的文献和1961年Vickrey提出基准点模型和收入等价原理以来，拍卖理论的研究体系已经形成并获得了相当丰富的研究成果［1－2］。相比而言，拍卖理论的实证研究却出现了较大的滞后。直至1992年Paarsch首次用结构计量方法分析经验拍卖数据，相关的技术方法才引起了广泛关注并且逐渐趋于成熟［3］。拍卖模型的结构计量方法以拍卖理论为指导，用以理解投标行为并提供政策建议，具有很强的理论意义。而现实生活中有大量可以获取的经验拍卖数据，如政府采购，国债销售，牌照的发放，工程项目的招标，房产、土地、农产品、艺术品的拍卖等。因此可以说，拍卖理论实证研究有较大的应用前景。

根据私有估值的分布是否已知为有限维参数的函数，主流的拍卖模型的结构计量方法主要有三种：分段的伪最大似然估计（Piecewise Pseudo－Maximum Likelihood Estimation，PPMLE）［4－5］。 模 拟非线性最小二乘估计（Simulated Nonlinear Least Square，SNLS）和非参数估计（Nonparametric Estimation）［6－7］。其中，非参数方法与前两者不同，它在估计的过程中不需要求解均衡策略的具体形式，而且事先不需要任何参数假设，有着参数方法不可比拟的优点，得到越来越多学者的青睐。Athey和Haile用非参数方法研究了不同标准拍卖模型的可识别性以及每个模型的信息结构［8］。Brendstrup和Paarsch考虑了投标人不对称情形下带保留价的荷兰式拍卖的非参数结构估计［9］。当既有第一价格拍卖的数据又有第二价格拍卖的数据时，Lu和Perrigne给出了识别投标人效用函数的非参数方法，并用美国林务局的木材拍卖数据作了实证分析［10］。Bajari和Hortacsu使用非参数方法估计了第一价格拍卖的四个模型（风险中性模型、风险规避模型、学习模型和投标的量子响应模型）的结构参数，对每个模型得出的估计值与实际值作了对比，发现风险规避模型能得到更为合理的估计［11］。

为此，本文把第一价格拍卖的非参数估计方法推广到风险规避的情形，并总结了简单的估计过程。为验证估计效果，本文用模特卡罗模拟实验对其进行分析和评价。针对风险规避参数估计量的不确定性，本文提供了多种选择。另外，为提高风险规避参数估计量的实用性，本文通过对比模拟实验的效果给出了一些指导性的建议。

二、风险规避模型

考虑对称独立私人价值模型中风险规避情形的第一价格拍卖（包括第一价格密封拍卖和降价拍卖），假设不存在最低保留价。设有n个买方竞拍某个不可分割的物品，规定赢者是出价最高的投标方且支付价为其投标价。如果不止一个投标方出价相同且最低，则拍品以随机的方式进行分配。假设投标方对物品的私有估值vi（i＝1，2，…，n）是连续型随机变量，它独立同分布于共同函数F（·），且概率密度f（·）定义在区间］上。另外假设每个买方都是风险规避的，其效用U（·）为von Neuman Morgensten函数，且满足U′（·）＞0，U″（·）≤0和U（0）＝0。为便于讨论，不妨设私有估值v独立同分布于［0，1］上的均匀分布，其效用为不变相对风险规避（CRRA）函数，即U（x）＝xγ，γ∈［0，1］，其中γ＝1时对应为风险中性的情形。

令bi＝σ（vi）为投标方i的均衡投标函数，其分布函数和密度函数分别记为G（bi）和g（bi）。在弱正则条件下均衡投标函数是严格递增和可微的，因此其逆函数vi＝σ－1（bi）存在且与均衡投标函数有相同的性质。考虑第i个投标方的期望效用：

最大化上述期望效用得到一阶条件：

因为私有估值v为独立同分布于［0，1］上的均匀分布，所以F（vi）＝vi，f（vi）＝1，把它们代入上式得：

解上述微分方程可得均衡投标函数：

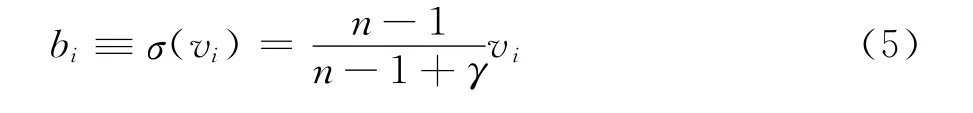
三、非参数结构估计

（一）估计过程

目前，相关的讨论往往把均衡投标价b看作是私有估值v的函数，而现实的拍卖数据一般来说只知道投标价而不知私有估值，因此本文考虑用投标价b表示私有估值v。故一阶条件式（2）又可表示成：

考虑T次类似的单物品拍卖，所有参与拍卖的投标人数根据数目的不同可分为N类，这些类构成一个有限集S，其元素个数即为N.本文采用Campo S等人的研究成果，用分位数的思想估计风险规避参数［12］。令vα表示第α个私有估价分布F（·）的百分位数，bα表示G（·）的第α个百分位数，则对任意不同的投标人数。于是，式（7）可表示成分位数的表达式：

上述两个方程做减法运算可以得到如下的表达式：

（二）估计量的选择

上式在的上标中，a代表第一种权重，b代表第二种权重。

风险规避参数最优估计量的选择受许多因素的影响，如拍卖次数、投标人数等。事实上，没有明显的证据显示某个估计量会优于另一个。本文利用模特卡罗模拟实验对不同集成估计量的性能进行验证。在此之前，总结风险规避情形下的非参数估计过程如下：

从悦读草堂到思源堂，可以让我们深刻地感受到学校对民族文化的传承，也许这与学校所处的位置有关系，但也折射出我国台湾地区教育在文化熏陶方面的共性。

第1步：在已知可观测投标价｛bit，i＝1，… ，n，t＝1，… ，T｝的基础上，使用非参数方法估计均衡投标价的概率分布函数G（·）和密度函数g（·），估计过程中用到经验分布和核密度估计量：

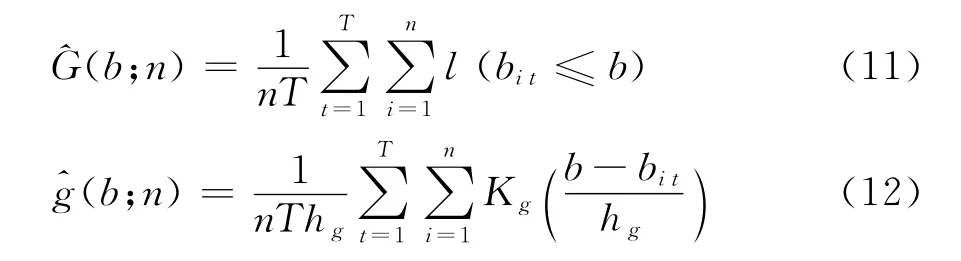
其中1（·）为示信函数，h g是带宽，K g（·）是核函数，详细内容参见Hardle W专著中的非参数估计方法和核估计量［13］43－80。

第2步：根据（10）式及选择的权重分别计算风险规避参数的四个集成估计量。

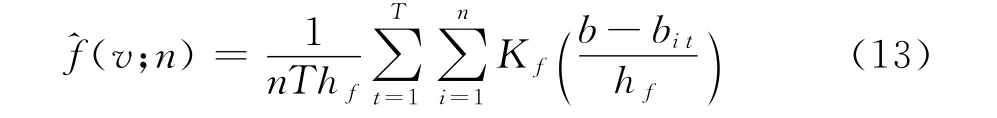
其中h f是带宽，K f（·）是核函数。

四、实验设计与讨论

（一）实验设计

在私有估值和风险规避参数的真值未知的情况下，蒙特卡罗模拟实验通常是评价其估计性能的理想方法，本文也采用这种方法［7］。在所有的模拟实验中，投标者的私有估值服从［0，1］上的均匀分布，其效用函数为U（x）＝xγ，γ∈ ［0，1］。为考虑风险规避的不同情形，实验取10个不同的风险规避参数值γi＝0.1×i（i＝1，2，…，10），其中γ10对应风险中性的情形。为最大程度地模拟真实拍卖数据，考虑三种不同的样本容量T：400、2 000和8 000，分别对应于小、中、大样本。每个样本中投标人数n∈S＝｛3，6，9，12｝，它们在不同样本容量T中所占的比例p（n）分别以平均、递增和递减的三种趋势进行分配（记为设计A、设计B和设计C），详见表1。

表1 三种实验设计方案

为得到模拟的拍卖数据，本文首先根据表1中三种不同的设计按均匀分布随机抽取相应的私有估值，然后根据方程（5）计算不同风险规避参数下的投标价①数据集的生成过程类似于文献［7］，不同之处在于后者只考虑风险中性的情形。。需要说明的是，本实验中的随机数是由乘同余方法（multiplicative congruential method）生成，其模为（231－1），乘子为397 204 094，初始种子为2 420 375。为了最小化噪声对实验结果的影响，实验过程重复1 000次。

另外，在非参数估计过程中，核函数K（·）的选取满足标准假设。具体来说，令核函数K（u）＝（35／32）（1 －u2）31（｜u｜≤ 1）， 带 宽h g＝分别为投标价和私有估值的标准差。然而核密度估计量（·）在边界处是渐近有偏的，这说明在投标价的边界和处对应于可观测投标价的私有估值的估计是有问题的。为了解决这个问题本文沿用Guerre E等人研究成果中的方法，在第2步关于私有估值的估计过程中对可观测的投标价进行了简单的修剪，剪掉近似10%的观测值。

（二）结果与讨论

根据方程（10）可知，分位数α的选择对风险规避参数γ的估计有一定的影响，而且由于利用非参数方法并不能十分准确地估计g（·），特别是在样本较小的情形下，这进一步加剧了分位数α对风险规避参数γ的影响。因此，为最小化这种影响程度，本文对分位数α进行了一定的优化。具体来说，本文令α∈ ｛0.9，0.91，…，0.99｝②我们也考虑了分位数α∈ ｛0.8，0.81，…，0.89｝，甚至更小的情形，但实验结果表明将α限定在0.9至0.99之间，绝大部分情形下可以得到更好的效果，而且不会由于α的候选值过多导致优化过程的计算量过大。，优化的目标是使得所有估计的风险规避参数的方差最小，本文给出的所有结果都是对分位数α优化后得到的。

限于篇幅，本文只给出γ2，γ5和γ10的估计结果，详见附表5～13③由于表5 13的篇幅较大，这里从略，请对此研究感兴趣的读者通过编辑部索要或与作者联系索取。。从这些表中容易看出，估计得到的四种风险规避参数γ的均值和中位数都比较接近真实值，特别是在样本容量T较大时。由此可知，使用本文给出的风险规避情形下的非参数估计过程得到的估计效果总的来说还是不错的，这说明本文给出的非参数估计过程是可行的，同时也验证了非参数估计对数据量的需求比较大的理论。对于样本容量较小的情形，设计A得到的估计效果要远好于其他两种设计。本文认为这与不同的投标人数在样本容量T中所占的比例有关，这个比例如果差别很大就会导致方程（8）与方程（9）中的vα不再相等，从而使方程（10）中的等号成立变得有些牵强。

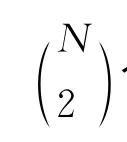
表2 选择集成估计量的指导性建议

另外，为评价本文提出的非参数估计过程对投标人私有价值的估计效果，定义估计私有估值和实际私有估值的距离为：

其中＾vit和v it分别表示第t次拍卖中投标人i的估计和实际私有估值。根据表2选择的风险规避参数估计量，计算得到的相关结果见表3。分析表3中估计的私有估值和实际的私有估值之间的距离，不论其均值、中位数还是标准差都比较小，这说明私有估值的估计效果也是不错的，特别是对大样本来说。

五、结 语

本文在投标者的私有估值服从均匀分布，效用函数为CRRA函数的基础上，总结了风险规避情形下第一价格拍卖的非参数结构估计过程。为验证估计过程的可行性，本文用模特卡罗模拟实验对其效果进行了分析和评价。为最大程度地模拟真实拍卖数据，实验取10个不同的风险规避参数值（包括风险中性的情形），考虑了小、中、大三种不同的样本容量，并对投标人数在样本容量中的比例做了平均、递增和递减三种设计。实验结果显示无论是风险规避参数还是私有估值，它们的估计效果总体来说都是不错的。针对估计过程中风险规避参数估计量不唯一的缺点，本文提供了估计量的多种选择。同时，为提高估计过程的实用性，通过对比模拟实验的效果给出了估计量选择的一些指导性建议。

表3 估计私有估值和实际私有估值的距离

［1］ Friedman L.A Competitive Bidding Strategy［J］.Operations Research，1956，4（1）.

［2］ Vickrey W.Counterspeculation，Auctions，and Competitive Sealed Tenders［J］.Journal of Finance，1991，16（1）.

［3］ Paarsch H.Deciding between the Common and Private Value Paradigms in Empirical Models of Auctions［J］.Journal of Econometrics，1992，51（1／2）.

［4］ Donald S G，Paarsch H J.Piecewise Pseudo－Maximum Likelihood Estimation in Empirical Models of Auctions［J］.In ternational Economic Review，1993，34（1）.

［5］ Donald S G，Paarsch H J.Identification，Estimation，and Testing in Parametric Empirical Models of Auctions Within the Independent Private Values Paradigm ［J］.Econometric Theory，1996，12（3）.

［6］ Laffont J J，Ossard H，Vuong Q.Econometrics of First－Price Auctions［J］.Econometrica，1995，63（4）.

［7］ Guerre E，Perrigne I，Vuong Q.Optimal Nonparametric Estimation of First－Price Auctions［J］.Econometrica，2000（3）.

［8］ Athey S，Haile P.Identification of Standard Auction Models［J］.Econometrica，2002，70（6）.

［9］ Brendstrup B，Paarsch H J.Non－Parametric Estimation of Dutch and First－Price，Sealed－Bid Auction Models with Asymmetric Bidders［R／OL］.［2009－05－8］.Working Paper，University of Iowa Department of Economics，2003.http：／／paarsch.ecom.unimelb.edu.au／download／dutch.pdf.

［10］Lu J F，Perrigne I.Estimating Risk Aversion from Ascending and Sealed－Bid Auctions：The Case of Timber Auction Data［J］.Journal of Applied Econometrics，2008，23（7）.

［11］Bajari P，Hortacsu A.Are Structural Estimates of Auction Models Reasonable？Evidence from Experimental Data［J］.Journal of Political Economy，2005，113（4）.

［12］Campo S，Guerre E，Perrigne I，Vuong Q.Semiparametric Estimation of First－Price Auctions with Risk Averse Bidders［R／OL］.［2010－08－10］.Working Paper，Pennsylvania State University，2006.http：／／econ.la.psu.edu／～iup2／forthcoming／CGPV4.pdf

［13］Hardle W.Smoothing Techniques with Implementations in S［M］.New York：Springer－Verlag，1991.

Nonparametric Estimation Method for Risk Aversion Case in First－price Auction

AN Xin1，2，LIU Shu-lin2

（1.School of Economics and Management，Beijing Forestry University，Beijing 100083；2.School of International Trade and Economics，University of International Business and Economics，Beijing 100029）

In many literatures on auction empirical studies，more and more clues show that the bidders indeed tend to risk averse.However，current many auction quantitative methods only consider the case of risk neutrality.In order to solve this problem，the nonparametric estimation method of the first－price auction is generalized to the risk aversion case，several estimators of risk aversion parameter are given，and then a simple estimation procedure is summarized.Finally，Monte Carlo simulation experiments are utilized to evaluate the estimation performance.The experimental results show that the proposed nonparametric estimation method can work well in estimating the risk aversion parameter as well as private valuations，thus verifying the effectiveness of the method.At the same time，some guidance on selecting the estimator of risk aversion parameter is given on the basis of the Monte Carlo simulation experiments.

first－price sealed－bid auction；risk aversion；nonparametric estimation；Monte Carlo simulation

（责任编辑：张治国）

O212.2

A

1007－3116（2011）11－0089－06

2011－03－25；修复日期：2011－06－22

对外经济贸易大学优秀博士学位论文培育基金项目《拍卖计量模型理论与实证研究》（73600002）

安欣，女，山东临沂人，经济学博士，讲师，研究方向：数量经济学。

【统计应用研究】