动臂式塔机变截面吊臂的整体稳定性分析

张宏生，陆念力

(哈尔滨工业大学机电工程学院，哈尔滨150001，hszhanghit@gmail.com)

塔式起重机(简称塔机)广泛应用于高层建筑施工、大型设备吊装等诸多领域，在建筑施工中是无可替代的.动臂式塔机的吊臂通过俯仰变化来实现变幅，吊臂在吊重和变幅绳的共同作用下，近似只承受轴向压力，因此吊臂的整体稳定性一直是设计人员关注的焦点.动臂式塔机吊臂的结构特点是由变截面的根部段、头部段以及等截面的中间段组成的非等截面混合结构，吊臂通过根部铰与塔身连接，变幅钢丝绳固定在吊臂头部.故在起升平面内，吊臂的支撑形式可简化为简支式，在起升平面外为悬臂式.

对于等截面柱和几种简单的变截面柱的稳定性，Timoshenko［1］给出精确解.为了准确地分析由变截面段和等截面段组成的非等截面混合结构稳定性，很多学者进行了研究.Rahai［2］使用修正的振动模态法和能量法研究了非等截面混合结构的稳定性.Bazeos［3］根据变截面不同变化率和不同边界条件得到无量纲化的欧拉临界力图表，然后利用插值法快速计算结构的欧拉临界力.楼梦麟［4］提出了基于Ritz展开的模态摄动法来求解变截面压杆稳定性问题的半解析方法.在使用有限元方法进行分析时，单元刚度阵的准确性直接影响计算结果.对于等截面梁，文献［5］从弯曲微分方程出发得到精确的Bernoulli-Euler梁单元的刚度阵.由于变截面梁的复杂性和多样性，很多学者提出了各种变截面梁单元［6-10］，一般来说，很难获得统一的精确刚度阵.对于阶梯柱模型，文献［11］使用等截面梁精确有限元法得到了阶梯柱的递推公式.在起重机设计规范GB/T 3811-1983中将变截面柱等效为修正计算长度的等截面柱，对于变截面段和等截面段组成的非等截面混合结构稳定性，只考虑了变截面段对称的这一特殊情形.

本文从多节阶梯柱的挠度微分方程出发，应用传递矩阵法，研究了简支梁模型和悬臂梁模型这两种支撑形式，得到多节阶梯柱模型欧拉临界力控制方程的表达式.使用各节长度相等的多节阶梯柱模型模拟变截面柱，对于由变截面柱和等截面柱组成的非等截面混合结构，可统一为多节阶梯柱模型.

1 多节阶梯柱的传递矩阵法

如图1所示的n节阶梯柱模型，其中Li为第i节柱顶端到根部的长度，Ii为第i节柱的截面惯性矩，L为多节阶梯柱总长，P为顶部轴力，E为弹性模量.

图1 多节阶梯柱模型

对于分段等截面梁模型，可列写第i节柱的挠度微分方程为

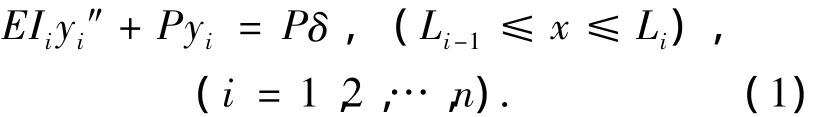
式中:L0=0，Ln=L，δ为顶部位移.

方程(1)的通解为

由边界条件x=Li时，yi=yi+1且y'i=y'i+1，得到

记

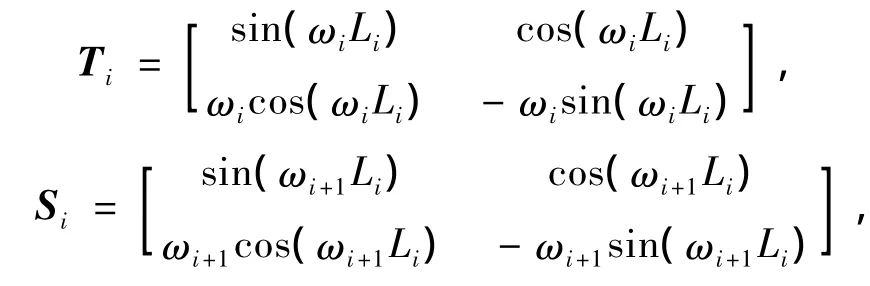
式(3)可表示为

记

式(4)可表示为

因此可得到传递矩阵关系为

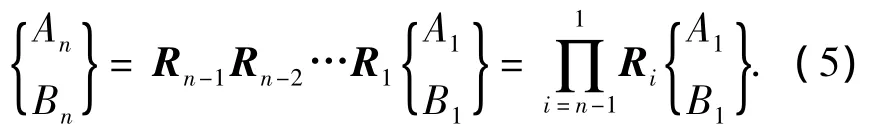
当δ=0时，式(1)和(2)即为简支梁模型的挠度微分方程及其通解，不难证明，对于简支梁模型的待定系数仍将满足式(9)传递矩阵关系.

悬臂梁模型的根部边界条件为y1(0)=0且y'0(0)=0，解出

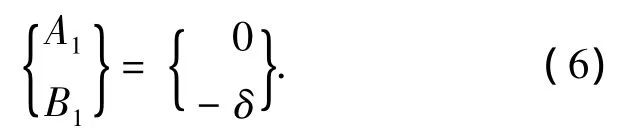
简支梁模型的根部边界条件为y1(0)=0，解出

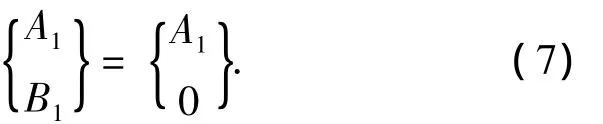
悬臂梁模型的顶部边界条件为yn(L)=δ，简支梁模型的顶部边界条件为yn(L)=0，可统一表示为

由式(8)和式(5)可获得临界失稳特征方程为

应用边界条件(6)或(7)可分别求出悬臂梁模型或简支梁模型的欧拉临界力.需要指出的是，本文推导的求解多节阶梯柱的欧拉临界力的传递矩阵法，既没有限制每节柱的长度，也没有限制每节柱的截面惯性矩，也未包含任何附加假定，对多节阶梯柱模型来说，本文方法得到的临界载荷P的控制方程式(9)是精确的.

2 计算结果与比较

本文将变截面梁柱以n节长度相等的非等截面阶梯柱来模拟，随着分节数目的增多，多节阶梯柱模型计算结果将趋近于精确解.对几个经典算例进行稳定性分析，来验证本文方法的准确性.为了便于比较，引入量纲为一的稳定系数m=PcrL2/EI2.

在计算过程中，为了简化计算，式(6)和式(7)中可以取δ=-1和A1=1.每节阶梯柱使用各节变截面两端惯性矩的中间值，计算结果较为精确，推荐使用

其中Ii和Ij分别为每小节变截面柱的两端惯性矩.

例1 图2所示为截面惯性矩为4次变化的变截面柱，a为反映截面锥度的常数，I1/I2=1/2，a/(a+L)=(1/2)1/4.图2(a)为悬臂梁模型，其精确的欧拉临界力［1］为Pcr=2.002EI2/L2;图2(b)为简支梁模型，其精确的欧拉临界力［1］为Pcr=6.979EI2/L2，使用本文多节阶梯柱的传递矩阵法，分成n节长度相等的非等截面阶梯柱来计算欧拉临界力，计算结果比较如表1，2所示.

图2 截面惯性矩按四次变化的变截面柱

表1 截面惯性矩四次变化悬臂梁模型稳定系数m值

表2 截面惯性矩四次变化简支梁模型稳定系数m值

例2 图3所示为截面惯性矩按2次变化的变截面柱，a为反映截面锥度的常数，I1/I2= 3/10，a/(a+L)=(3/10)1/2.图3(a)为悬臂梁模型，其精确的欧拉临界力［1］为Pcr=1.763EI2/L2;图3(b)为简支梁模型，其精确的欧拉临界力［1］为Pcr=5.622EI2/L2，使用本文多节阶梯柱的传递矩阵法，分成n节长度相等的非等截面阶梯柱来计算欧拉临界力，计算结果比较如表3、4所示.

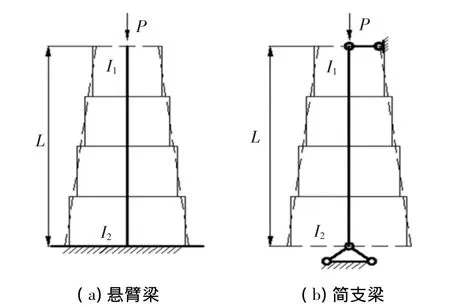
图3 截面惯性矩按二次变化的变截面柱

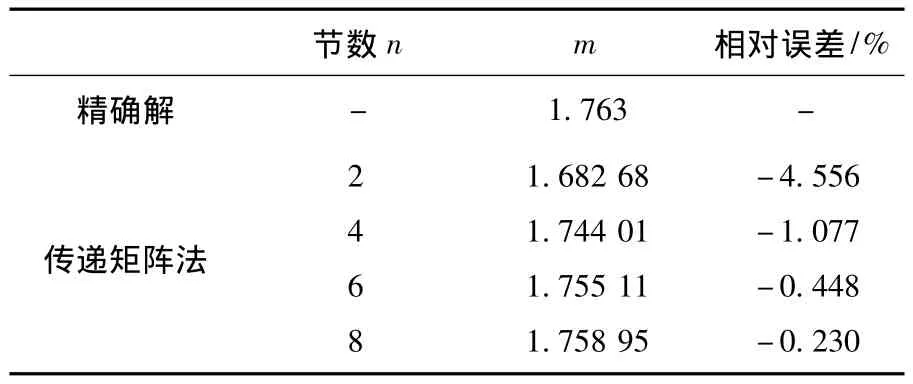
表3 截面惯性矩二次变化悬臂梁模型稳定系数m值

表4 截面惯性矩二次变化简支梁模型稳定系数m值

其中表1～4的精确值来自文献［1］，从表中可以看出，本文多节阶梯柱传递矩阵法的计算精度很高，用6节阶梯柱模拟变截面柱求解整体稳定性，将得到很好的计算结果，误差均小于0.5%.

例3 某动臂式塔机吊臂模型如图4所示，由a、c两段惯性矩按2次变化的变截面段和b段等截面段组成，图4(a)为平面内简支式整体稳定性计算模型;图4(b)为平面外悬臂式整体稳定性计算模型.La=0.2L，Lc=0.3L，Ia1/Ib1=0.3，Ic1/Ib1=0.4，Ib2/Ia2=0.9，Ic2/Ib2=0.4.引入无量纲稳定系数 m1= PcrL2/EIb1和 m2= PcrL2/EIa2，使用通用有限元软件 ANSYS中的Beam44变截面梁单元，并将各段分为10～80个单元，对于平面内和平面外两种模型，由ANSYS计算得到m值如表5所示.使用本文多节阶梯柱的传递矩阵法，等截面段只分为1节，变截面段分为2～6节，计算结果如表6所示，其中表6中相对误差比较的对象为使用ANSYS将每段分为80个单元得到的解.

图4 动臂式塔机吊臂模型

表5 动臂式塔机吊臂模型ANSYS计算稳定系数m值

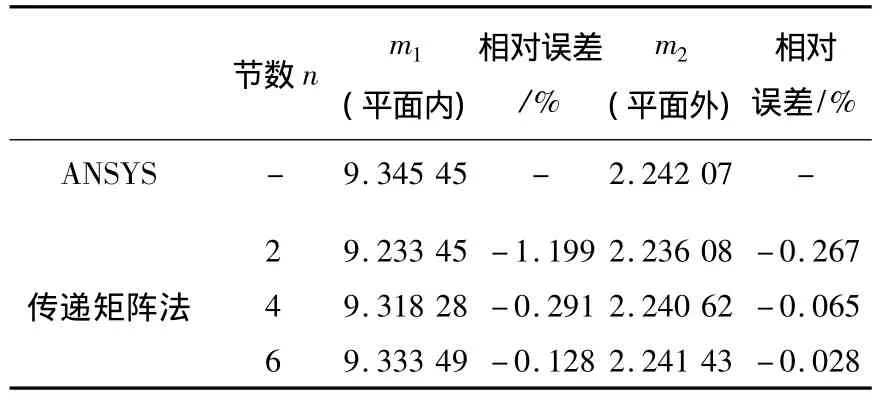
表6 动臂式塔机吊臂模型稳定系数m值

3 结论

1)本文推导的求解多节阶梯柱欧拉临界力的传递矩阵法，对多节阶梯柱模型，该方法是精确的.当使用该方法以多节长度相等的非等截面阶梯柱来模拟变截面柱，会产生误差，但是随着划分节数的增多，误差逐渐减小.

2)本文推荐将每段变截面柱划分为6节长度相等的非等截面阶梯柱，求解整体稳定性的欧拉临界力误差小于0.5%，精度很高.对于变截面和等截面组成的非等截面混合结构，其等截面段只需划分为1节，变截面段划分为6节将得到满意的结果.

［1］TIMOSHENKO S P，GERE J M.Theory of elastic stability［M］.New York:McGraw-Hill，1961:134-141.

［2］RAHAI A R，KAZEMI S.Buckling analysis of non-prismatic columns based on modified vibration modes［J］. Communications in Nonlinear Science and Numerical Simulation，2006，13(8):1721-1735.

［3］BAZEOS N，KARABALIS D L.Efficient computation of buckling loads for plane steel frames with tapered members［J］.Enineering Structures，2006，28(5):771-775.

［4］楼梦麟，李建元.变截面压杆稳定问题半解析解［J］.同济大学学报，2004，32(7):857-860.

［5］陆念力，兰朋，李良.二阶理论条件下的梁杆系统精确有限元方程及应用［J］.哈尔滨建筑大学学报，1998，31(4):67-74.

［6］LI Guo-qiang，LI Jin-jun.A tapered Timoshenko-Euler beam element for analysis of steel portal frames［J］. Journal of Constructional Steel Research，2002，58: 1531-1544.

［7］BAKER G.Exact deflections in nonprismatic members［J］.Computers＆Structures，1996，61(3):515-528.

［8］郭彦林，王文明，石永久.变截面门式刚架结构的非线性性能［J］.工程力学，2000，17(4):29-36.

［9］卞敬玲，王小岗.变截面压杆稳定计算的有限单元法［J］.武汉大学学报，2002，35(4):102-104.

［10］宋启根，徐梁，宋丹.变截面梁柱刚度方程的Bessel函数解［J］.计算力学学报，2001，18(3):355-357.

［11］陆念力，兰朋，白桦.起重机箱形伸缩臂稳定性分析的精确理论解［J］.哈尔滨建筑大学学报，2000，33(2):89-93.