具有多条最短路径的最短路问题
2010-03-14王志坚韩伟一李一军
王志坚,韩伟一,李一军
(哈尔滨工业大学管理学院,哈尔滨150001,wyhan@mails.gucas.ac.cn)
单源点正权最短路问题是最短路问题中最简单的、应用最为广泛的一类问题,在计算机科学、交通科学等工程技术领域具有非常重要的应用. Shimbel[1]提出了第一种算法——矩阵算法,但计算效率较低,计算复杂性为O(n3logn).长期以来,Dijkstra算法一直是解决正权单源点最短路问题的最好算法之一[2],该算法既可用于有向问题,又可用于无向问题,应用Fibonacci堆计算复杂性为O(m+nlogn)[3-7].然而,它只能求得从源点到其它点的一条最短路径,最终结果表现为一棵最短路径树.事实上,从源点到指定点可能存在多条最短路径,Dijkstra算法无法给出所有的最短路径.为了方便,本文把这类从源点到指定点存在多条最短路径的问题特称为具有多条最短路径的最短路问题.如果源点和指定点仅仅存在数量不多的最短路径,获得这些最短路径不存在实质性难度,可以通过枚举列出.如果源点和指定点间的最短路径数量庞大,则无法一一列出,只能从中选出若干条较满意的最短路径,如所选择的最短路径具有最少的边数等[8-10].为此,本文将对Dijkstra算法进行修正,修正后的算法得到的不再是最短路径树,而是最短路径图.在最短路径图中,从源点到指定点的任意两条路径都具有相同的距离.文中还将基于最短路图,应用Yen算法罗列出从源点到指定点的所有最短路径.
1 修正的Dijkstra算法
单源点正权最短路问题可描述为:给定一个具有n个点xi(1≤i≤n)、m条边的有向图或无向图G(V,E),令源点为v1,边(vi,vj)的权w(vi,vj)为正实数.若点v为图中任意一点,R是G(V,E)中从v1到v的一条路径,定义路径的权是所有边的权之和,记为w(R).单源点最短路问题就是在所有从v1到v的路R中,求一条权最小的路R0使得w(R0)= {w(R)}.
经典 Dijkstra算法是一种标号算法,其思想为:
1)引入了两种标号,即T和P.T为从源点v1到v的最短路权的上界,称为临时标号,记为T(v).P为从源点v1到这一点的最短路权,称为固定标号,记为P(v).之所以称为固定标号,是因为当点v拥有P后,其T的值就不再改变.同时,引入集合S,用以表示所有具有P的点的集合.
2)引入函数λ(v),用以记录路径R中点v的上一个点.
3)首先令源点v1的T(v1)=0,其它点v的T(v)=+∞,并令源点v1首先成为具有P的点,同时把点v1加入到集合S.算法的每一步总能使一个没有P的点转变为新的具有P的点,这样一来,经n-1步,所有点都将拥有P,算法终止.这时候,点v的P就是从源点v1到v的最短路权.
4)根据函数λ(v),反溯得到从源点v1到v的最短路径.
Dijkstra算法的具体步骤为:
Step.1 初始化.
T(v1)=0,λ(v1)=v1;T(v)=+∞,
λ(v)=M;S=φ.
Step.2 选取不拥有P但具有最小T的点y,同时令P(y)=T(y),S=S∪{y}.
Step.3 对所有未进入集合S的、点y的邻点x进行T更新过程.即:
如果T(y)+w(y,x)<T(x),那么T(x)= T(y)+w(y,x),同时令λ(x)=y.
Step.4 如果所有点都进入集合S,那么算法停止,根据函数λ(v)得到从源点v1到v的最短路径,否则转入Step.2.
应用Dijkstra算法可以求得最短路径树.在最短路径树中,从源点到任意点仅仅只有一条最短路径,这条路径在原图中则表现为相应两点之间的一条最短路径.下面给出修正的Dijkstra算法为:
Step.1 初始化.
T(v1)=0;μ(y,x)=0;R={v1};S=φ.
Step.2 在集合R中选取具有最小T标号的点y,则:
1)S=S∪{y},R=R-{y};
2)若边(y,x)∈E且x∉S,则R=R∪{x}.
Step.3 若边(y,x)∈E,则:
情形1 若T(y)+w(y,x)<T(x),则T(x)=T(y)+w(y,x),μ(y,x)=1;
同时若μ(z,x)=1且z≠y,则μ(z,x)=0.
情形2 若T(y)+w(y,x)=T(x),则μ(y,x)=1.
Step.4 如果所有点都进入集合S,那么算法停止,把所有μ(y,x)=0的边从图G(V,E)中删去,这样得到的新图就是最短路径图,记为G#,在G#中从源点v1到v的任意一条路径都是原图G(V,E)中从源点v1到v的最短路径,此时的T(v)就是从源点v1到v的最短路径的权;否则转入Step.2.
修正的Dijkstra算法相对于经典的Dijkstra算法得到的不再是最短路径树,而是最短路径图.在最短路径图中,从源点到指定点的任意一条路径在原图中均是最短路径.修正的Dijkstra算法具有:1)本改进算法仅保留了Dijkstra算法的T标号,简化了Dijkstra算法;2)在Dijkstra算法的初始化步骤中,令T(v)=+∞,这给计算机编程实现带来了困难,不得不选定一个足够大的数来代替+∞,本文的算法可避免这个麻烦.
下面给出算法正确性的证明:
引理1 在修正的 Dijkstra算法中,如果T(y)+w(y,x)=T(x),那么必有μ(y,x)=1.
证明 根据算法的Step.3,当T(y)+w(y,x)<T(x)或T(y)+w(y,x)=T(x)时,都将有μ(y,x)=1且T(y)+w(y,x)=T(x).而当T(y)+w(y,x)>T(x)时,由算法的Step.3,μ(y,x)的值不发生变化,由于每个点仅进行一次T更新过程且μ(y,x)的初始值为0,因而μ(y,x)的值仍然为0.另一方面,根据算法的Step.3,点y的T过程使得T(z)+w(z,x)=T(x)不再成立,情形1将令μ(z,x)=0,从而保证了只有当T(y)+w(y,x)=T(x)时,μ(y,x)的值才可能为1.
综合上述几种情形,当μ(y,x)=1时,T(y)+ w(y,x)=T(x)时,总有μ(y,x)=1.
定理1 修正的Dijkstra算法可获得从源点v1到点v的所有最短路径.
证明 假设P0=(v1,U1,…,Ui,…,Uh,v)是得到的从点v1到点v的任一条最短路径,而P1=(v1,Q1,…,Qi,…,Qr,v)是从点v1到点v的任意一条路径.
根据算法的步骤和引理1,对于路P0有

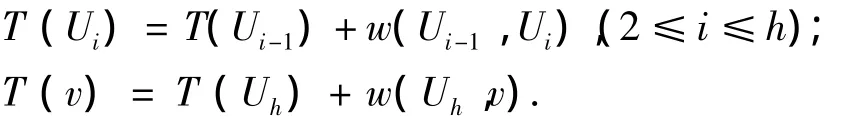
如果P1也是从点v1到点v的一条最短路径,那么必有
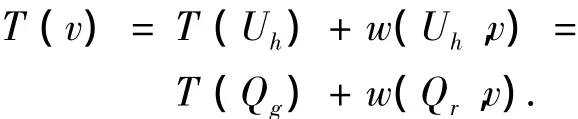
根据引理1,那么总有μ(Qr,v)=1.这样就保证了边(Qr,v)保留在最短路图中.同时,也必然有

否则P1就不是从点v1到点v的最短路径,这样也有μ(v1,Q1)=1且μ(Qi-1,Qi)=1(2≤i≤r),说明P1中的所有边都在最短路图中.
鉴于P1的任意性,因而修正的Dijkstra算法总可获得从源点v1到点v的所有最短路径,这些最短路径中的任意一边都保留在最短路图中.
定理1保证了算法的正确性.由引理1和定理1可直接得到:
推论1 在最短路图中,从点v1到点v的任一条路径都是原图中从点v1到点v的最短路径.
例1 求解下列最短路问题.
在例1中,显然从点1到点2~点8和点9都存在多条路径,应用经典的Dijkstra算法得到的最短路径树为:

而应用修正的Dijkstra算法,得到的最短路径图与原图相同.由最短路径图,从点1到点9将具有8条最短路径.例1的图规模较小,列出两点间的所有最短路径是容易的,而当图的规模庞大且两点间的最短路径的数目可观时,将不得不寻求专门的算法.
2 获得两点间的所有最短路径
应用修正的Dijkstra算法得到一个最短路径图.该算法基于最短路径图可以获得从源点到指定点的所有最短路径.该算法的思想是,根据各最短路径中边的数目对各最短路径进行排序,边数越少的最短路径对应的级别就越高,算法将按照级别由高到低的顺序依次列出所有的最短路径.
如果令最短路径图中的各边的权均为1,那么从源点到指定点的路径长度和路径中的边数相等.这样一来,从源点到指定点的路径长度越短,该路径的级别就越高.按照级别由高到低依次列出所有的最短路径,可以借助于求解第k条最短路径问题的Yen算法来解决[11].
设从源点到指定点有多条路径,这些路径具有不同的长度,如果按照长度由小到大进行排序,那么第k条最短路径是指排在第k个位置的路径.Yen算法是求解无圈第k条最短路径问题当前公认的最好算法.Yen算法的思想是,首先求得从源点到指定点的第1,2,…,k-1条最短路径,然后在这k-1条最短路径的基础上求得第k条最短路径.由于在最短路径图中,从源点到指定点的最短路径是有限的,因而当k足够大时,按照Yen算法总可以求得从源点到指定点的所有最短路径.
下面给出获得所有最短路径的算法为:
Step.1 应用修正的Dijkstra算法得到最短路径图G#.
Step.2 令最短路图G#中所有边的权均为1,得到新的图G*.
Step.3 应用经典的Dijkstra算法得到图G*的从源点到指定点的最短路径,也就是第1条最短路径.
Step.4 令k=2.
Step.5 应用Yen算法求得图G*的从源点到指定点的第k条最短路径.如果Yen算法无法得到第k条最短路径,则算法结束,否则转入Step.6.
Step.6 k=k+1,转入Step.5.
由于从源点到指定点的最短路径的数目是有限的,因而算法是收敛的.事实上,在算法的Step.3就得到了从源点到指定点的、边数最少的一条最短路径.
例2 求解下列最短路问题,求得从点1到点9的所有最短路径.

解:应用修正的Dijkstra算法得到最短路径图.

由最短路径图,可知从点1到点9具有多条最短路径,最短路径的长度为20.接下来,令最短路径图的各边的权均为1,得到:

在最短路径图上,应用Yen算法得到从点1到点9的所有最短路径为:
第1条最短路径:1→2→9;
第2条最短路径:1→4→2→9;
第3条最短路径:1→4→5→9;
第4条最短路径:1→3→4→5→9;
第5条最短路径:1→3→4→2→9;
第6条最短路径:1→4→6→7→8→9;
第7条最短路径:1→3→6→7→8→9;
第8条最短路径:1→3→4→6→7→8→9.
3 结论
1)对Dijkstra算法进行了修正,修正后的算法得到的不再是最短路径树,而是最短路径图.
2)对Dijkstra算法进行了简化,不再沿用P标号仅仅保留了T标号,在初始化步骤中也不再令各点的T标号的值为无穷大,客观上为算法的计算机实现提供了方便.
3)基于最短路径图,应用求解第k条最短路径的Yen算法,根据边数由少到多可依次给出从源点到指定点的所有最短路径.
[1]SHIMBEL A.Structure in communication nets[C]// Proceedings of the Symposium on Information Networks. New York:Polytechnic Press of the Polytechnic Institute of Brooklyn,1955:199-203.
[2]DIJKSTRA E W.A note on two problems in connexion with graphs[J].Numerische Mathematik,1959,1(1):269-271.
[3]FREDMAN M L,TARJAN R E.Fibonacci heaps and their uses in improved network optimization problems[J].Journal of the ACM,1987,34(3):596-615.
[4]NOSHITA K,MASUDA E,MACHIDA H.On the expected behaviors of the Dijkstra’s shortest paths algorithm for complete graph[J].Information Processing Letters,1978,7(5):237-243.
[5]NOSHITA K.A theorem on the expected complexity of Dijkstra’s shortest paths algorithm[J].Journal of Algorithms,1985,6(3):400-408.
[6]PETTIE S,RAMACHANDRAN V.Computing shortest paths with comparisons and additions[C]//Proceedings of the 13th Annual ACM-SIAM Symposium on Discrete Algorithms.Philadelphia:Society for Industrial and Applied Mathematics,2002:267-276.
[7]PETTIE S,RAMACHANDRAN V.A shortest path algorithm for real-weighted undirected graphs[J].SIAM Journal on Computing,2005,34(6):1398-1431.
[8]孙强,杨宗源.求受顶点数限制的最短路径问题的一个算法[J].计算机工程,2002,28(9):73-74.
[9]周经纶,吴焕群.受顶点数限制的最短路径问题及其算法[J].系统工程,l996,l4(5):37-44.
[10]MARFINS V E Q.On a multicriteria shortest path problem[J].European Journal of Operational Research,1984,l6(2):236-245.
[11]YEN J Y.Finding the K shortest loopless paths in a network[J].Management Science,1971,17(11):712-716.
