空间飞网捕获机器人交会轨迹规划研究

翟 光，梁 斌，李 成

(1.哈尔滨工业大学控制科学与工程系，哈尔滨150001，gzhai@robotsat.com;2.北京理工大学飞行器设计，北京100081)

与一般的交会对接任务不同，由于飞网捕获装置弹射迅速，有效捕获距离远，近距离接近轨迹末端不需要进行相对停靠和位置保持，因此只要接近轨迹飞掠过目标，且轨迹中存在满足小于捕获距离的点，同时能够避免进入禁飞区域内即可.正是基于这种相对运动中捕获目标的思想，本文提出一种基于多脉冲机动的飞掠型安全轨迹方案，使空间飞网捕获机器人在近距离接近过程中逐渐进入有效捕获范围并在相对运动过程中捕获目标，考虑安全接近轨迹的基本约束条件，飞掠型多脉冲安全轨迹设计方案如图2所示.

空间飞网捕获机器人系统是一种基于飞网的新型在轨目标捕获系统，可广泛地应用于空间碎片清理、失效航天器辅助变轨等领域［1-2］.空间飞网捕获机器人在接近待捕获目标的交会过程中，如何规划设计接近轨迹并保证系统自身安全，是交会轨迹规划中重点解决的问题.对于交会轨迹规划问题，Pressing J.E［3-4］和Jezewski D.J［5-6］研究了一般交会条件下的交会轨迹规划方法，文献［7-10］研究了多目标约束条件下交会轨迹规划问题.本文将采用线性规划的方法，以燃料消耗最少和防碰撞安全条件作为规划约束设计一种多脉冲被动安全接近轨迹，一方面使规划得到的标称轨迹能够避免与目标发生碰撞，另一方面当轨控发动机失效或者测量设备发生故障时，从标称轨迹上任意点开始的自由漂移轨迹能够使空间飞网捕获机器人漂离目标并自主退出任务，并且其自由漂移轨迹同样是安全的，本文最后将对轨迹规划结果进行仿真，验证标称轨迹和自由漂移轨迹的安全特性.

1 航天器相对动力学模型

如图1所示，首先建立目标航天器的轨道坐标系，坐标系原点位于目标航天器的质心，XT轴指向航天器飞行方向，ZT轴指向地心与航天器质心连线方向，YT轴与其他两轴构成右手坐标系垂直于轨道平面方向.rt和rc分别表示由目标航天器和追踪航天器质心指向地心的矢量，ρ表示由追踪航天器质心指向目标航天器质心的矢量.目前航天器相对动力学模型应用较为广泛的为CW方程，它是一种航天器相对运动的线性化方程表示形式.由于这个方程与G.W.Hill在1878年研究月球相对地球运动时得到的方程类似，因此也有很多人将此方程称为Hill方程.根据开普勒方程，追踪航天器和目标航天器分别运行在近圆轨道上，忽略空间环境当中的各种摄动作用，并假定地球引力场为中心引力场，则追踪航天器和目标航天器的轨道运动方程分别为

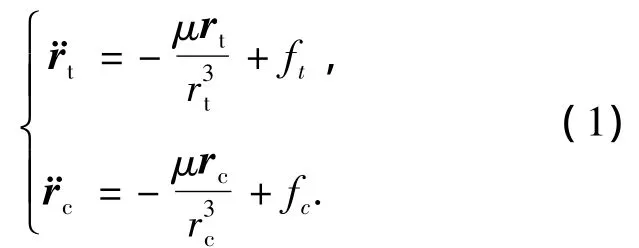
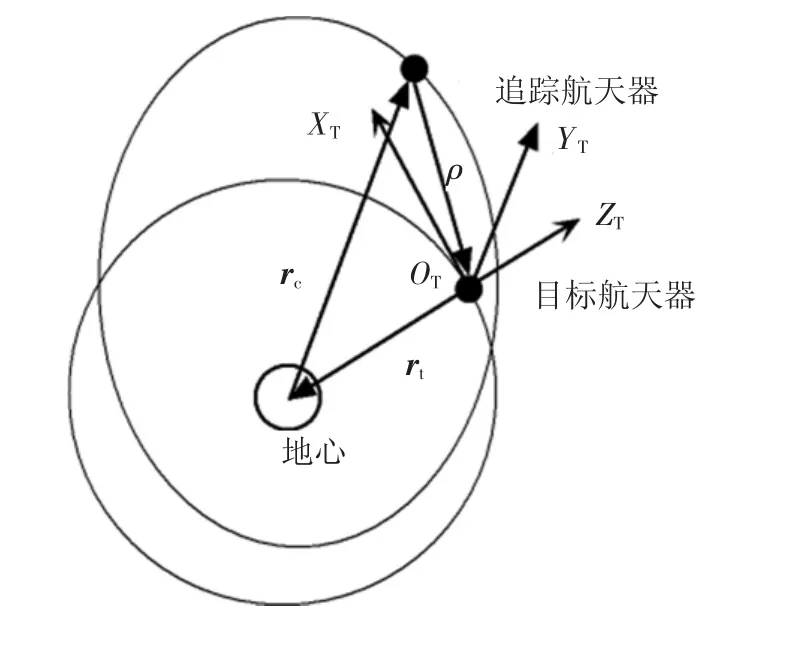
图1 航天器相对运动示意图

式中，rt表示目标航天器的位置矢量，rc表示追踪航天器位置矢量，μ为地球引力常数，ft和fc分别为目标航天器与追踪航天器的控制力.在目标航天器轨道坐标系中根据矢量对时间求导法则有

式中右侧第一项为追踪航天器在动坐标系当中的相对径向加速度，第二项为动坐标系转动相关的向心加速度，第三项为动坐标系转动角速度变化相关的加速度，第四项为哥式加速度.由式(1)有

在目标星轨道坐标系下有 ρ=［x，y，z］T，rt=［0，0，rt］T，ω =［0，-ω，0］T，当两航天器相对距离远小于目标航天器轨道半径时，两者之比的二阶项可以略去，将式中括号内的幂函数进行泰勒展开，只保留一阶小量，式(2)可以简化为

设a=［ax，ay，az］T为各项加速度分量，联合式(2)和式(3)有

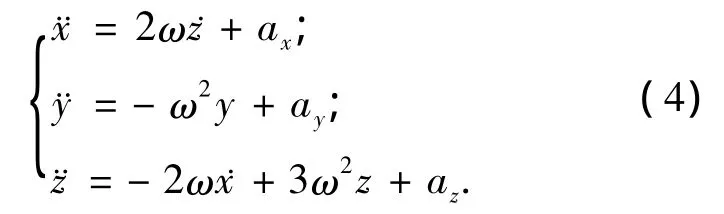
式(4)便是C-W方程的线性模型，简称Hill方程.工程应用证明在两航天器相对距离小于50 km的情况下，该线性化模型具有足够的精度.本文的轨迹规划将基于上述动力学模型进行.

2 被动安全轨迹规划

近距接近轨迹的安全是指在发动机和目标测量故障的情况下，空间机器人在接近过程中不会与目标飞行器发生碰撞.安全轨迹设计的关键是定义安全区域，即在目标飞行器外围定义一个禁止进入的区域.安全区域的定义可以根据误差因素、目标飞行器尺寸、安全系数等因素确定.安全轨迹即指不进入安全区域的接近轨迹，安全轨迹规划就是通过给定机动起始时刻两航天器的相对状态、接近过程的时间约束、机动脉冲次数等参数，确定接近轨迹的机动策略.

目前安全轨迹设计模式一般分为两种，包括主动安全模式和被动安全模式.如果追踪航天器在接近过程中需要执行碰撞机动操作则为主动安全模式;如果追踪航天器的无控条件下自由漂移轨迹不进入安全区域则为被动安全模式.相对而言被动安全模式能够最大限度的保证轨迹的安全特性，同时也能够减少控制操作，因此本节将采用被动安全模式来设计多脉冲接近轨迹.

2.1 安全轨迹的基本约束

空间飞网捕获机器人安全接近轨迹设计要综合考虑接近轨迹起始点相对状态、目标跟踪测量、飞网弹射捕获位置等因素.接近轨迹的起始点相对状态是指实施近距接近机动初始时刻的相对位置和相对速度，考虑到机器人系统在实施近距接近机动之前需经历相对停靠状态以对目标实施跟踪伴飞，结合轨道相对动力学的特点，选取v-bar作为跟踪方向最为合理;在近距离接近过程当中，空间飞网捕获机器人的相对测量设备应保持对目标连续跟踪测量，为保证可见光相机和激光测距仪能够正常工作，就应该避免地影出现在测量设备的视场之内，使目标测量设备视场背景保持“干净”;此外根据后继章节的分析，受重力梯度力矩的影响，空间机器人在完成目标捕获后成为一空间绳系系统，其姿态只有在r-bar方向才能保持稳定，且由轨道动力学扰动造成的捕获偏差最小，因此飞网弹射捕获点应尽量设计在r-bar方向.假设接近轨迹的起始点相对状态为［x0，y0，z0，˙x0，˙y0，˙z0］T，轨迹终点的相对状态为［xT，yT，zT，˙xT，˙yT，˙zT］T，接近过程中的任意点状态为［xt，yt，zt，˙xt，˙yt，˙zt］T，则安全接近轨迹的基本约束可以表示为

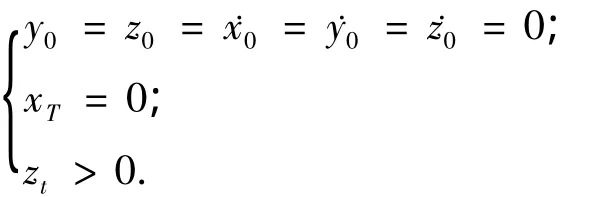
2.2 多脉冲飞掠型安全轨迹的设计

与一般的交会对接任务不同，由于飞网捕获装置弹射迅速，有效捕获距离远，近距离接近轨迹末端不需要进行相对停靠和位置保持，因此只要接近轨迹飞掠过目标，且轨迹中存在满足小于捕获距离的点，同时能够避免进入禁飞区域内即可.正是基于这种相对运动中捕获目标的思想，本文提出一种基于多脉冲机动的飞掠型安全轨迹方案，使空间飞网捕获机器人在近距离接近过程中逐渐进入有效捕获范围并在相对运动过程中捕获目标，考虑安全接近轨迹的基本约束条件，飞掠型多脉冲安全轨迹设计方案如图2所示.

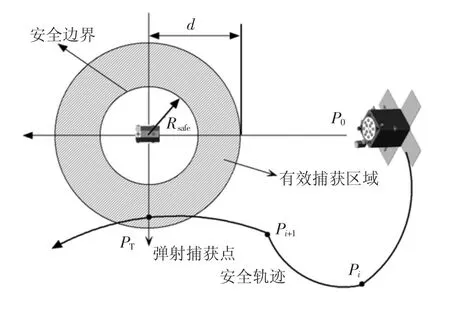
图2 飞掠型多脉冲安全接近轨迹

图2中P0为安全轨迹的起始位置，PT为飞网弹射捕获位置，Pi和Pi+1表示相邻的两个机动脉冲施加位置，d为最大有效捕获距离，Rsafe为圆形安全区域边界的半径，空间机器人在经过多个脉冲机动后由P0点到达PT点，适当的选择PT点在r-bar方向的位置，可以达到调整安全轨迹有效捕获段的时间长度的目的.

为同时满足目标捕获约束和轨迹安全约束，飞掠型多脉冲安全接近轨迹首先须保证通过脉冲机动，接近轨迹能够进入有效的捕获范围;其次接近轨迹任意点能够避免进入禁飞区域;最后接近轨迹必须能够保证在任意机动脉冲施加之后，空间飞网捕获机器人长时间自由漂移轨迹不进入禁飞区域;此外在近距接近时间约束和脉冲个数确定的条件下，轨迹规划的结果应尽量减少机动过程中的燃料消耗.

安全轨迹规划是一项较为复杂的工作，在进行安全轨迹设计之前，必须首先明确安全轨迹规划约束条件的数学描述形式，建立安全轨迹规划的数学模型并求解.本文接下来将采用线性规划的方法，首先以速度增量最优为目标函数，然后建立飞掠型多脉冲安全接近轨迹的线性规划数学模型，最后通过数学仿真验证安全轨迹设计的合理性.

2.3 多脉冲速度增量最优机动

由于本文考虑的捕获过程定义在轨道平面内，且平面外运动与平面内运动解耦，因此可忽略y项运动.忽略各种外力扰动，由式(4)可得面内相对运动具有以下形式:

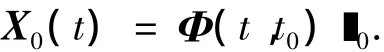
其中状态转移矩阵各部分与整体转移状态矩阵各部分相对应，整体转移矩阵可以表示为

X0=［x0，z0，˙x0，˙z0］T为系统的初始状态，τ=ω(t-t0).从近距接近机动开始点P0到飞网弹射捕获点 PT，系统的状态将由［x0，z0，˙x0，˙z0］T变为［xe，ze，˙xe，˙ze］T.采用N脉冲机动方式，假定由P0至Pe耗时T，则有

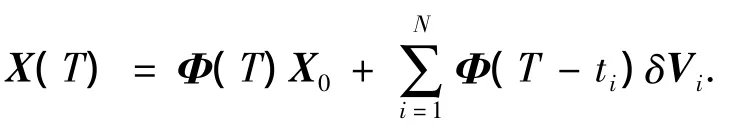
式中:ti为第i个脉冲施加时刻的时间，δVi=［0，0，δ˙xi，δ˙zi］T为施加的第i个速度脉冲.为便于给出安全捕获轨迹规划的约束条件，将式写成分量的形式有

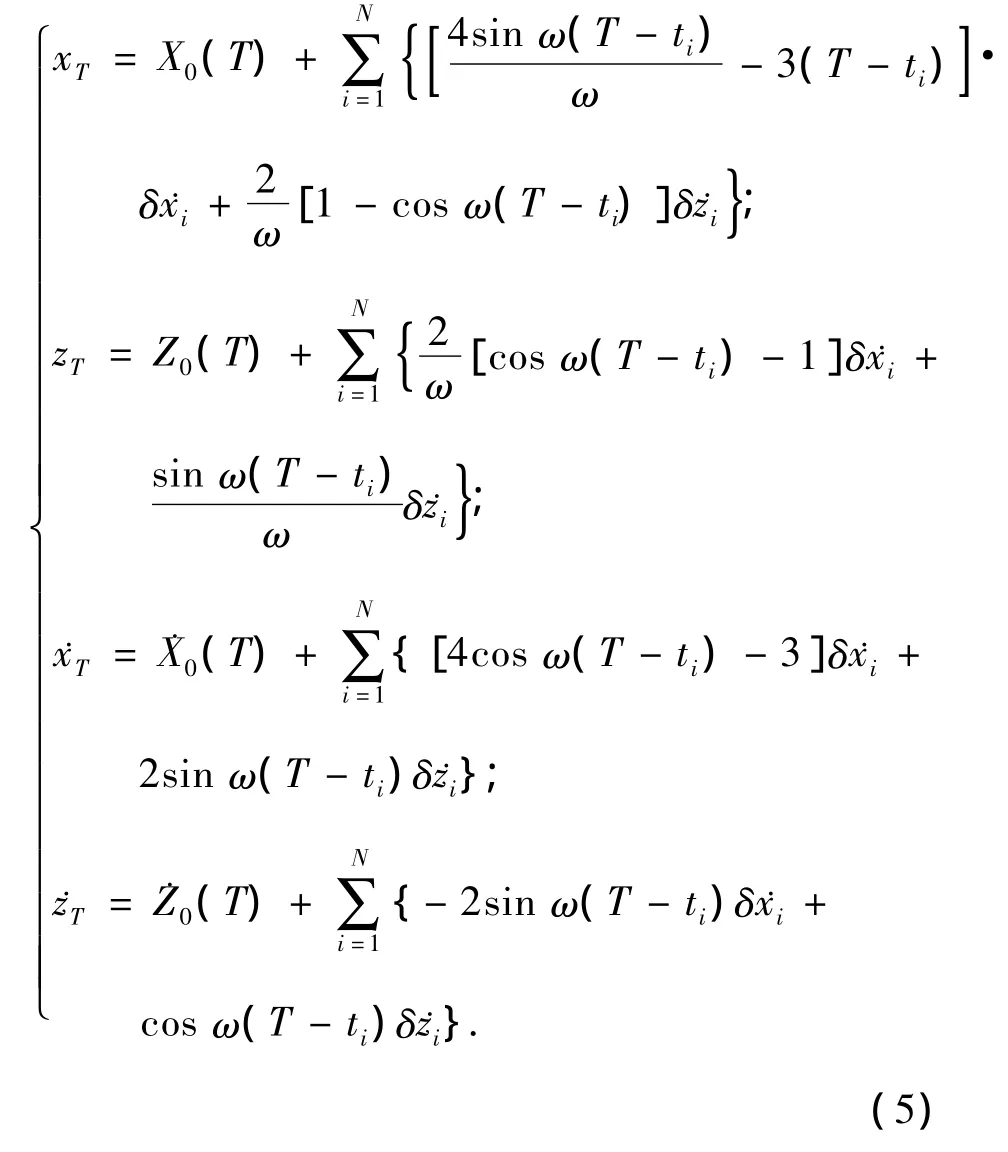
式中:X0(T)、Z0(T)、˙X0(T)、˙Z0(T)可由下式求得

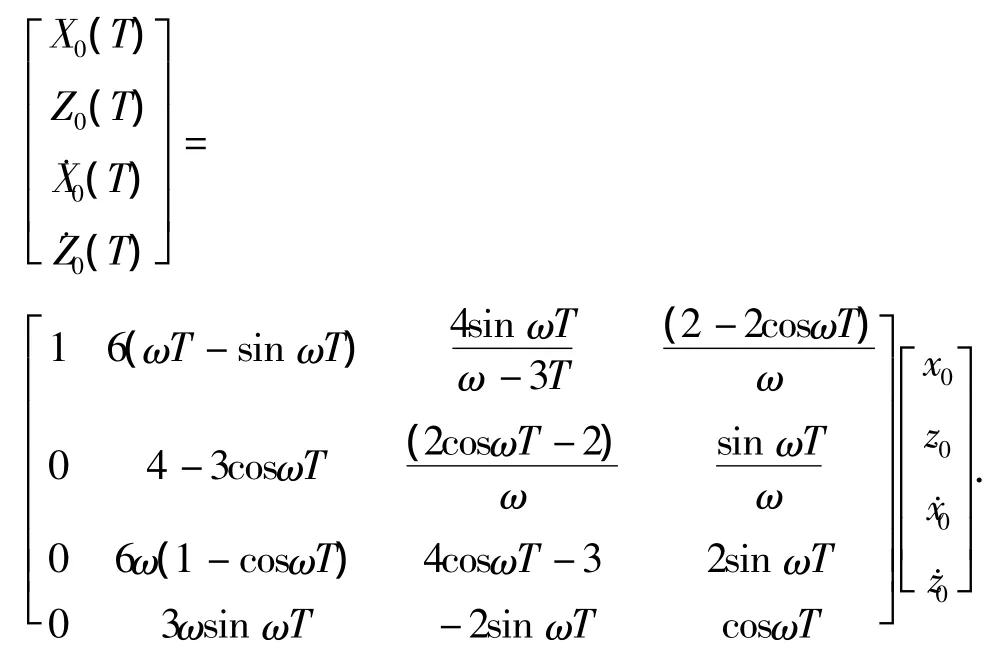
上式便是系统的N脉冲相对运动方程，从式中可以看到系统的状态变化和系统的初始状态及所施加的速度脉冲增量有关，所施加的速度脉冲和各个状态分量的运动形式呈线性关系.

在近距接近过程中，空间机器人目标测量设备的视线轴方向应该连续指向目标航天器，系统本体坐标系与轨道坐标系将呈一定的夹角，因此在轨道坐标系内的x和z向速度脉冲增量可通过六自由度轨控发动机脉冲合成得到.设速度脉冲增量的合成形式如图3所示，即总速度脉冲增量可以分解为4个脉冲速度分量，并且4个脉冲速度分量均非负.此时为了求最小速度脉冲增量安全轨迹，则首先定义安全轨迹规划的速度脉冲增量优化目标函数，即

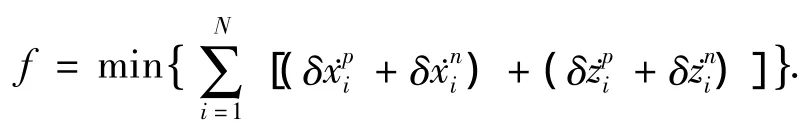
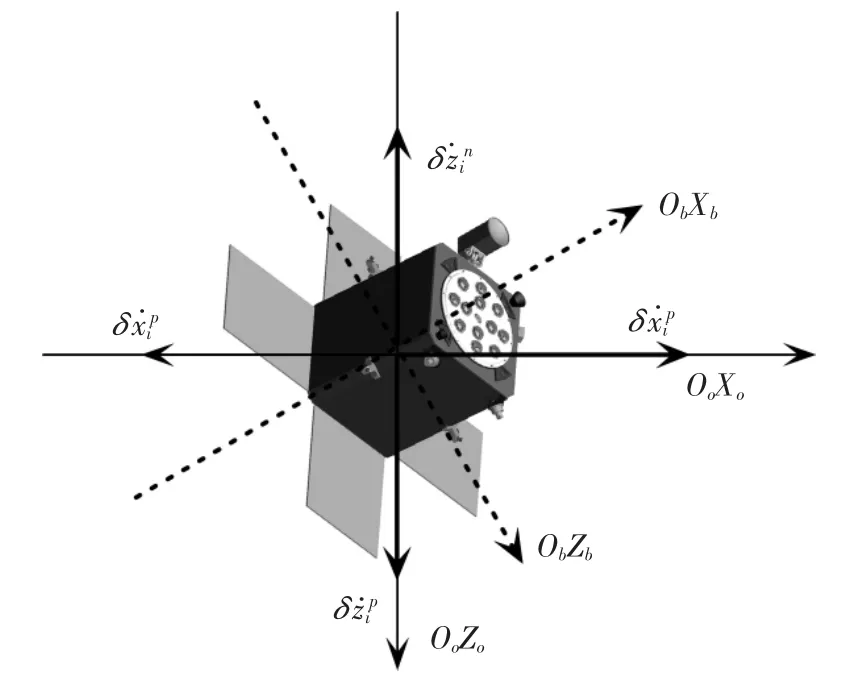
图3 速度脉冲分解图

2.4 飞掠型轨迹的安全约束条件

设系统的初始位置为P0点，弹射捕获点为PT点，系统在经过N次脉冲机动后在T时刻到达弹射捕获点.下面分段考虑交会轨迹的安全约束条件.首先考虑从第2个脉冲至第N个脉冲段，显然只要在执行任意脉冲后其短期和长期漂移轨迹位于‖z(t)‖≥Rsafe平面区域内即可保证整个轨迹的安全性，本文的长期漂移考察时长定义为一个轨道周期.进一步根据式(5)考察z向相对运动的特性，由于z向相对运动不含长期发散项，因此根据z向相对运动的周期性，其长期漂移安全约束可以转化为一个轨道周期内的安全约束，具体的做法可在执行脉冲机动后一个轨道周期内选择足够大的M个等间隔时间点，使任意时刻有‖z(t)‖≥Rsafe，显然M越大轨迹的安全性保障就越充分.若捕获点PT位于z＞0平面内，则有

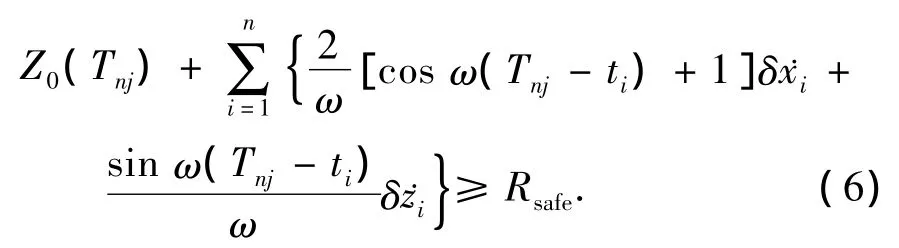
其中:n=1，2，…，N;j=1，2，…，M×(N-1).

在施加第N个脉冲后安全轨迹需在T时刻经过PT点，设PT点的位置矢量为［x(T)，z(T)］T，则弹射捕获点对轨迹的约束条件可表示为

进一步考虑第一个脉冲和第二个脉冲之间的轨迹段约束条件.为了保证交会轨迹满足式(6)的约束，第一个脉冲施加后指定时刻T1必须使系统进入到z(t)≥Rsafe平面区域，且其长期漂移轨迹满足安全性要求.为避免长期发散项使问题复杂化，可根据式(5)使第一个脉冲施加后系统相对运动轨迹为一封闭椭圆，此时δ˙x1=0，δ˙z1≠0，则约束条件可写为

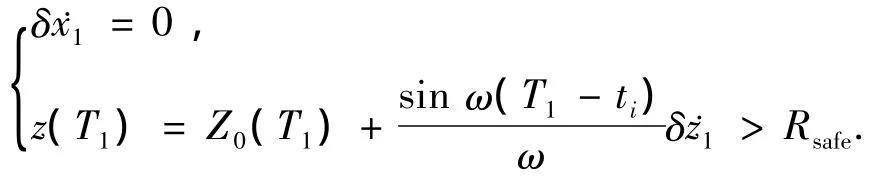
称上式为第一脉冲约束.由于施加第一个脉冲后系统的相对运动轨迹为一封闭椭圆，根据椭圆轨迹的特性，其在x向最大的位移可由椭圆的长半轴确定，当椭圆的长半轴与安全轨迹边界无交点时，第一个脉冲的长期漂移轨迹为安全轨迹，因此第一脉冲约束可分为以下两种约束条件:

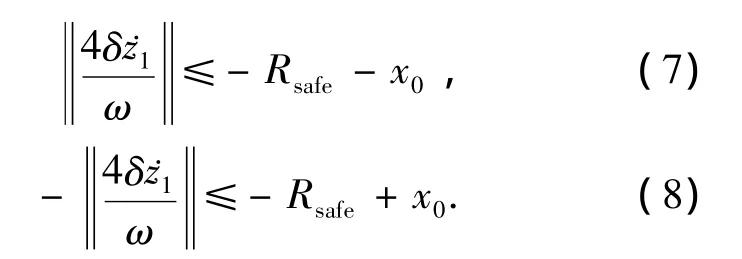
2.5 安全轨迹线形规划标准型

通过上述推导可以看出，所有含速度脉冲的约束条件都是线性等式或者不等式，因此安全轨迹规划问题可以转换为线性规划问题求最优解，线性规划算法求解快速，非常适合于航天器在轨实时自主规划.经整理，捕获任务中的轨迹规划问题可表示为如下形式:

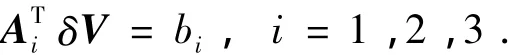
其余为不等式约束，通过不等式变换可以记为

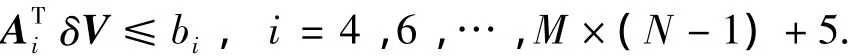
因此上述线性规划当中共有M×(N-1)+5个约束条件，线性规划中的最优解求取关键在于首先找到初始基本可行解，然后通过进一步迭代寻优.

3 安全轨迹规划算例仿真

假定初始时刻目标航天器和飞网空间机器人同运行于轨道高度为593.5 km的圆轨道上，初始时刻两航天器在目标轨道坐标系中处于停靠状态.取Rsafe=50 m，d=100 m，弹射捕获点位置为［0 m，70 m］，由起始位置到达目标点的规划时间分别定为T=3 600 s和T=4 200 s，取中间点数M=36;脉冲施加时刻为规划时间的等分点.分别取施加脉冲次数为3，4，5三种情况进行仿真，仿真结果表明在施加脉冲次数为3时无规划结果，施加脉冲次数为5时脉冲速度增量明显变大，而取施加脉冲次数为4时仿真结果较为合理.取相对初始状态为［-1 000 m，0 m，0 m/s，0 m/s］，图4，5是在规划时间T=3 600 s和T=4 200 s，第一脉冲约束条件取不同值时4脉冲安全轨迹规划的结果，图中两个虚线大圆和小圆分别表示有效捕获范围边界和安全区域边界，星号表示脉冲施加的位置.

在规划时间取不同值和第一脉冲约束取不同条件的情况下，接近过程当中各次施加的脉冲大小也不同，在整个接近过程当中，相对运动速度的变化情况如图6，7所示.

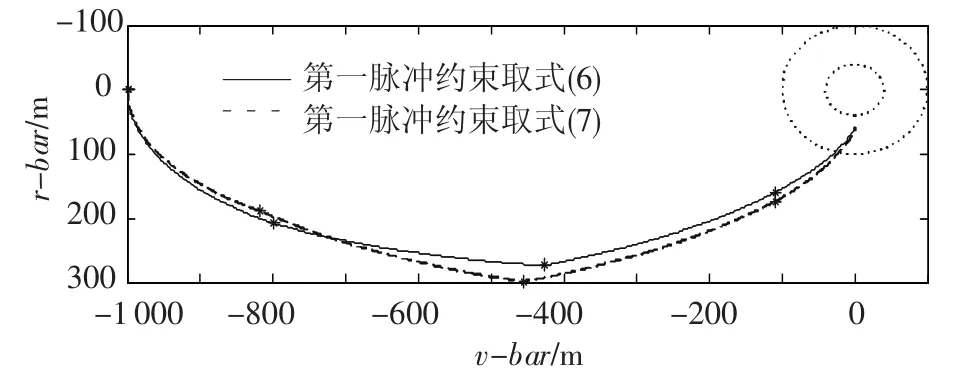
图4 T=3 600 s时的安全接近轨迹

图5 T=4 200 s时的安全接近轨迹

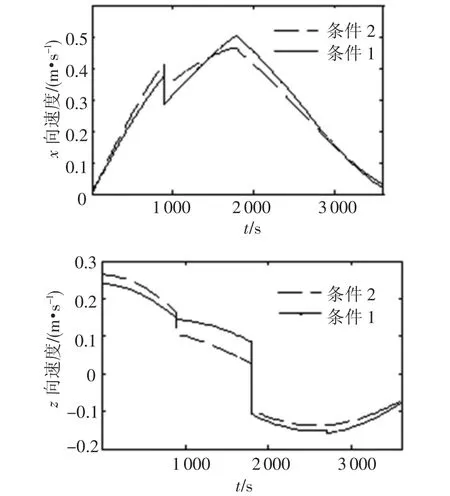
图6 T=3 600 s时x向和z向相对运动速度

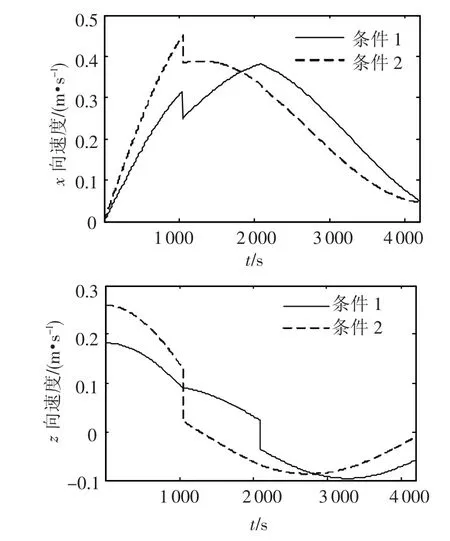
图7 T=4 200 s时x向和z向相对运动速度

为了对比在不同条件进行路径规划得到各次速度增量，分别取初始相对状态［-1 000 m，0 m，0 m/s，0 m/s］和［-2 000 m，0 m，0 m/s，0 m/s］两种情况，在不同规划约束条件下进行4脉冲规划并得到各次速度增量的大小，各次脉冲取代数和，其大小分别对应表1，2.

表1 初始距离1 km安全轨迹规划结果

表2 初始距离2 km安全轨迹规划结果

从表1，2的各次脉冲统计可以看出，在相同距离相同规划时间的约束条件下，第一脉冲约束取条件1的总速度增量要大于取条件2的情况;在第一脉冲约束条件相同时，规划时间T=3 600 s的总速度增量要大于T=4 200 s时的速度增量;而当初始相对距离增大时，总速度增量也随之增大.为进一步考察发动机故障情况接近轨迹的被动安全特性，以初始相对状态为［-1 000 m，0 m，0 m/s，0 m/s］为例，取规划时间T=3 600 s和 T= 4 200 s，第一脉冲约束取条件1，发动机在不同脉冲施加时刻失效后一个轨道周期的自由漂移轨迹.

为了进一步说明轨迹的被动安全特性，以T=3 600 s的安全轨迹规划为例，分别检验各脉冲施加后系统的自由漂移轨迹的安全特性，图中虚线给出了脉冲施加后一个轨道周期内的系统自由漂浮轨迹.图8，9为发动机在不同的脉冲施加处失效后系统的自由漂移轨迹，其中在第二个脉冲施加处发动机失效后的自由漂移轨迹为一周期性椭圆，T=3 600 s的情况下自由漂移轨迹离安全边界最近距离大约为272 m，T=4 200 s的情况下自由漂移轨迹与安全边界相切;第三和第四脉冲施加处发动机失效后自由漂移轨迹逐渐接近安全边界并最终漂离目标，显然上述规划得到的接近轨迹具有较好的被动安全特性.

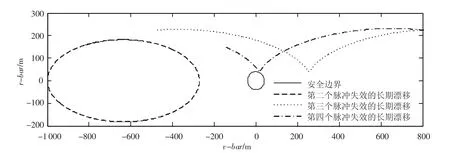
图8 T=3 600 s时四脉冲自由飘移轨迹

4 结论

本文首先推导了航天器相对运动的线性化模型，在考虑空间飞网捕获机器人自身安全和机动过程燃料消耗最优的条件下，提出了空间飞网捕获机器人安全捕获轨迹设计的概念和约束条件;设计了一种飞掠型近距离接近轨迹方案，推导了安全轨迹的不等式约束，以最小速度脉冲增量为目标函数，采用线性规划的方法建立了飞掠型安全轨迹的线性规划模型，该种设计方法在给定接近时间、脉冲机动次数、捕获位置等约束条件之后，能够快速给出各次机动脉冲大小，十分适合在轨捕获轨迹的实时规划;本文最后通过算例仿真，验证了在不同规划条件下轨迹规划方法的正确性和接近轨迹的安全性.

［1］ZHAI Guang，QIU Yue，LIANG Bin，LI Cheng.On-orbit capture with flexible tether-net system［J］.Acta Astronautica，2009，65:613-623.

［2］ZHAI Guang，QIU Yue，LIANG Bin，et al.System dynamics and feedforward control for tether-net space robot system［J］.International Journal of Advanced Robotic Systems，2009，65(2)，137-144.

［3］PRUSSING J E.Optimal four-impulsive fixed-time rendezvous in the vicinity of a circular orbit［J］.Journal of Spacecraft and Rockets，2003，40(6):952-959.

［4］PRUSSING J E.Optimal impulsive linear system:sufficient conditions and maximum number of impulses［J］. The Journal of the Astronautical Sciences，1995，43 (2):195-206.

［5］JEZEWSKI D J，DONALDSON J D.An analytic approach to optimal rendezvous using Clohessy-Wiltshire equations［J］.The Journal of the Astronautical Sciences，1979，27(3):293-310.

［6］JEZEWSKI D J，BRAZZELl J P.Survey of rendezvous trajectory planning［J］.Advances in the Astronautical Sciences，1992，76:1373-1396.

［7］WILLIAMS P.Prolonged payload rendezvous using a tether actuator mass［J］.Journal of spacecraft，2006，41:889-893.

［8］LUO Yazhong，TANG Guojin，LEI Yongjun.Optimal multi-objective linearized rendezous［J］.Journal of Guidance，Control and Dynamics，2007，30(2):383-389.

［9］FEHSE W.Automated Rendezvous and Docking of Spacecraft［M］.London:Cambridge University Press. 2003.

［10］YU Shaohua.On the dynamics and control of the relative motion between two spacecraft［J］.Acta Astronautics，1995，35(6):403-409.