数学概念生成性教学研究

摘要：概念教学是数学教学的重点和难点。重视数学概念生成性的教学有助于学生理解概念的本源和内涵。本文提出了数学概念生成性教学的三个策略：“问题链”式教学策略、追溯数学概念的本源性策略、教师主导学生主体互动策略。并以初中“函数”概念的教学为例，从概念引入环节、概念形成环节、概念剖析环节和概念扩展延伸环节阐述三个策略的应用，为数学概念生成性教学提供参考。

关键词：数学概念" 生成性教学" 初中数学" 函数

随着新课程改革的不断推进，培养学生的核心素养成为教育的一个重要目标。概念教学是数学教学的重点，也是难点，在学生数学素养培养方面具有重要意义。函数概念是初中数学基本的、重要的概念，同时也是高中数学的基础。函数概念具有高度的抽象性，教学过程中，如果只以教师为教学的主体，而学生的学习方式主要是题海战术，那么教学枯燥无趣，学生只能以被动的方式进行学习，不仅学到的知识有限，而且能力的提升也较为缓慢，制约了学生素养的发展。因此，教学中需要改变学生学习方法和教师教学方法，让每一位学生主动参与学习的过程，体验函数概念的产生过程，理论与实践有机结合，这样有助于学生更加深入地理解函数概念的本质。本文以初中“函数”概念的教学为例，探讨数学概念生成性教学。

一、概念生成性教学的内涵

学术界从不同角度对概念生成性教学的内涵进行了界定。从生成性教学的过程来看，教师通过向学生提供新的知识信息，可以给他们带来一定的刺激，促使学生将新的知识信息与原有的认知结构进行联系，在这个过程中，学生形成了关于新的知识信息的意义。从生成性教学的形态来看，它是一种在合适时机摒弃传统教学规则并进行灵活调整的教学形式。教师可以根据上课时师生互动情况，了解学生的学习行为并引导学生更好地消化和吸收课堂知识，让课堂教学始终充满活力。从生成性教学的角度来看，由于生成能力属于人类认知结构的基本功能，因此任何学生都有可能产生生成效果，这些效果体现为为学生提供发展机会，以及生成新的知识和意义。

综上所述，生成性教学是指，教师根据教学情况，在弹性预设的前提下，灵活且合理地设计教学活动，并在不断变化的动态教学形态中，推动学习者不断发展。

二、初中数学概念生成性教学的策略

（一）“问题链”式教学策略

在数学知识体系中，学生对概念性知识的掌握程度是后续学习的基础，有些概念贴近生活，很容易理解，有些概念离生活较远，难以理解，相对来说不易掌握，教师应采用生成性的教学方法，为抽象的数学概念提供生成条件，使学生以更能接受的方式理解和掌握所学的数学概念。“问题链”式教学法能够为此提供帮助，“问题链”式教学法指在教学过程中，教师按照教学目标将教学内容设置成以问题为纽带、以形成和发展学生思维能力为主线、以师生合作互动为基本形式的教学模式。

1.“问题链”式教学在数学概念生成中的作用

“问题链”式教学可以引导学生的思维层层递进，帮助学生从生活经验中抽象出数学概念，具体有多方面的作用。

第一，通过教师与学生的互动，生成性教学模式能够提升学生的参与度，从而增强学生的自觉性和主动性。与传统单向灌输的教学模式不同，生成性教学模式通过引导学生从抽象走向具体、从概念走向事实，让学生成为课堂的主体，深刻感受数学概念的形成过程。

第二，生成性教学模式能够增强教学的针对性。由于不同学生的基础知识和思维方式存在差异，设计问题链可以根据不同层次、不同思维水平的学生进行针对性的调整。这样能够让数学概念更贴近生活，贴近学生的原有认知水平，帮助学生更好地理解和生成数学概念。

第三，保证教学连贯性。设计问题链不是简单地将问题进行组合，问题是具有连续性的，能够起到承上启下的作用。初中阶段数学概念基本是从某个情境中生成的，情境作用的发挥离不开问题链的环环相扣，而且部分数学概念之间存在一定的联系。通过对数学概念进行细化、分解而形成问题体系，能够保证教学的连贯有序、层层递进，确保了数学概念生成过程中，形成严密的逻辑闭环。

2.“问题链”式教学数学概念生成的设计策略

“问题链”式教学要注重问题之间形成逻辑链条，通过设置学生感兴趣的问题激发学生的内驱力，并让问题环环相扣。教师围绕问题，引导学生积极探索数学概念的形成过程，营造良好的互动氛围，接下来笔者浅谈“问题链”式教学模式下数学概念生成的基本策略。

第一，“问题链”式教学可以提升学生对数学概念的感知能力。学生对数学概念的准确性、清晰性和完整性的把握，对于他们掌握基础知识、法则和公式等各种数学技能至关重要。“问题链”式教学通过设计一系列有机衔接的问题，引导学生从抽象走向具体、从概念走向事实，使学生深入感受数学概念的形成过程，从而提高他们对数学概念的感知能力。

第二，采用加强学生比较思维的策略，有助于提高数学概念形成过程中的理解能力。利用比较思维进行知识迁移，是常用的教学方法之一，在利用比较思维生成数学概念的过程中，也可以利用“问题链”式教学法实现教学目标。

（二）追溯数学概念的本源性策略

1.追溯数学概念本源性策略的作用

本源性问题往往隐藏在知识的背后，它具有一定的隐蔽性，所以数学概念的学习应围绕本源性问题展开，充分挖掘概念产生的背景，让学生理解学习数学概念的必要性和重要性，激发学生的好奇心和学习兴趣。数学学科中存在许多有着丰富历史背景与起源的概念，教师在具体的教学过程中，如果能够将这些历史背景与起源、数学故事进行巧妙的设计，必然激发学生学习数学概念的兴趣，学生通过追根溯源和探知前人的认知过程，自然也会对数学概念的本质产生更加深入的理解。

2.追溯数学概念本源性的设计策略

数学概念的生成离不开充分挖掘概念的产生背景，这就要求教师一方面在课堂上透过数学概念的表象，把握知识的本质，进而构建知识体系，使学生更好地掌握知识的本质，让学生明白概念产生的缘由；另一方面教师设身处地地从学生的角度思考问题。处于初中阶段的学生尚不具备充足的知识储备和一定的理解能力，教师要有前瞻性地将学生不理解的问题设计为本源性问题，引发学生思考。

（三）教师主导学生主体互动策略

1.教师主导学生主体互动策略的作用

在数学概念生成性教学中，为体现学生的主体地位，需要突出教学活动是在教师的引导下，学生充分参与课堂并自主探究，对教授的内容进行理解和感受，从而在学习中获得新的体验，达到数学概念的自主生成。

2.教师主导学生主体互动策略的设计

教师主导学生主体的互动策略需要教师创设问题情境，激发学生的创新思维，营造活跃的课堂氛围，适时开展合作交流，对学生的学习过程作出合理引导，从而取得教师主导学生主体的教学效果。

三、初中数学“函数”概念生成性教学设计

（一）概念引入环节

关于函数概念的引入，可以通过以下几个问题帮助学生进入课堂学习状态，引出本节课的重点。

问题一：老师去超市买苹果，发现苹果的单价是12元每千克，那么苹果净重和苹果总价有什么关系呢？

问题二：在期末考试中，成绩排行榜中有两个量：学号和成绩，那么一个学号能否有确定的成绩和它相对应？如果有，是一个还是多个？

问题三：同学们有看过《名侦探柯南》吗？其中有一个场景是警察根据案发现场的脚印长度和宽度，推断出犯罪嫌疑人的身高，这是什么原理呢？

通过这三个日常生活中大部分学生都见过，但并未对其中的道理进行深入思考的问题，引入本节课所讲解的函数概念。虽然这个时候学生并不能真正生成函数概念，但能在这三个问题中感受到我们日常生活中很多事情是存在一定规律的，如问题二中学号和成绩是一一对应的关系，一个学号对应着唯一的成绩，从而激发学生学习的主动性，并为后续概念生成打下良好的基础。

（二）概念生成环节

概念生成是教师提供丰富案例，让学生进行自主探究的过程。函数概念的生成，是基于学生对常量和变量概念的理解，此处主要采用教师主导学生主体的策略，使学生通过对实际问题的操作，体会数学在生活中的应用，帮助学生生成数学概念。

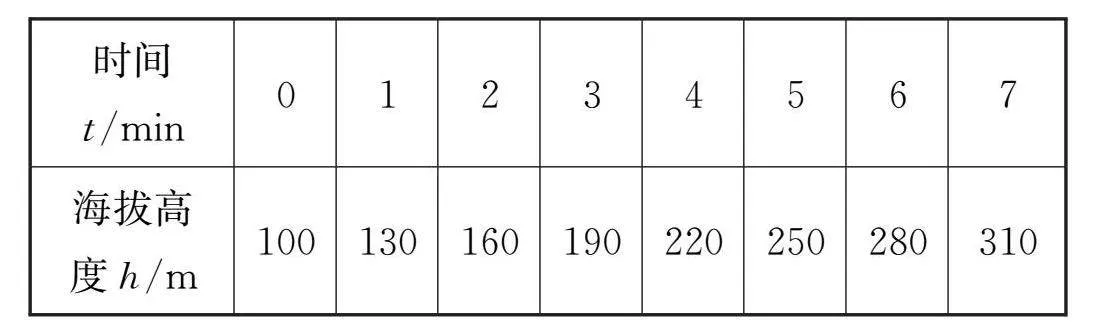
活动：播放热气球升空视频，并假设热气球从海拔100 m处的某地升空，在它逐渐上升的过程中，海拔高度h（m）与上升时间t（min）的关系记录如下：

（1）这次活动涉及哪几个量？

（2）观察表格中的数据，热气球升空的过程中速度为多少？

（3）哪些量发生变化？哪些量没发生变化？

（4）热气球高度随时间推移有什么变化规律吗？

（5）你能总结出h和t的关系吗？

（6）在上升时间为9 min和22 min时，热气球所处位置的海拔高度为多少米？

教师活动：组织学生集体交流，并寻找合适契机对表格中的数据进行分析。

该活动的（1）、（2）、（3）问通过学生对表格信息的讨论，容易得出热气球原来所在的高度、热气球上升的速度是不变的，热气球升空的时间和热气球海拔高度是发生变化的，这时教师可以引导学生总结常量和变量的定义，并掌握判断一个量是常量还是变量的方法。而（4）、（5）、（6）问帮助学生生成自变量和因变量的概念，从而得出函数的定义。

通过六个问题组成的“问题链”，让学生在自主探究与合作交流活动中，充分经历新知识的发生与发展过程，使学生有效地理解并掌握常量与变量、自变量与因变量及函数的定义。

（三）概念剖析环节

通过对教材的研读不难发现，函数单元的教学设计中情景教学居多，大部分是由实际问题抽象出相对应的函数问题，由此研究函数的概念，这有利于培养学生综合应用数学知识的能力和实践意识。然而在学习函数概念的过程中，教师或学生将侧重点经常放在后续研究函数的应用上，因此容易忽略函数自身内涵和外延的剖析。根据初中函数概念的定义：一般地，在一个变化过程中，如果有两个变量x和y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，我们就把x称为自变量，把y称为因变量，y是x的函数。教师可以引导学生剖析以下两个问题，帮助学生了解函数概念的内涵和外延。

问题一：在函数的概念中有“在某个变化过程中，有两个变量x、y”这一前提条件，请同学们根据这个条件，判断圆的面积公式S=πr2中，π和r是否可以构成函数关系。

问题二：为什么函数的定义是“在某个变化的过程中”？

以上两个问题，问题一帮助学生理解函数概念的外延，概念的外延是指具有概念所反映的特有属性的事物，通过让学生判断圆的面积公式中π和r是否可以构成函数关系，来考查学生对函数概念的外延是否充分掌握。问题二帮助学生理解函数概念的内涵，概念的内涵是指概念所反映的事物的特有属性，是概念必须具有的内容，那么可以通过一个具体的例子来解释问题二。在物理公式s=vt中，当时间是固定的一个值，那么速度与路程就构成了一个函数，速度越大则路程越长，在这个函数中，速度是自变量，路程是因变量，时间是常量；当速度是固定的一个值，那么时间和路程构成了一个函数，时间越长则路程越长，在这个函数中，时间是自变量，路程是因变量，速度是常量。综上所述，变量和常量都是相对于一个变化的过程而言的，没有绝对的变量和常量。

（四）课后拓展延伸环节（追溯概念本源）

学完函数概念，在教师布置的课后作业中，可以让学生查阅资料，了解人类为什么要创造函数。学生可以发现在16世纪和17世纪，欧洲资本主义国家为占领更多资源，不断发起战争，大力发展航运、武器等工业体系。而发展航运工业体系，就需要确定船只在海洋中的位置以及地球上的经纬度。同时在战争中想要取得胜利，也需知道如何向正确位置发射炮弹等一系列问题，这就促使人们需要对不同“运动”中的数量关系进行深入研究，这种历史背景为函数概念的产生提供了客观条件。

了解这些背景能够让学生更清楚地认识到数学概念不是凭空产生的，而是通过发现问题并经过仔细研究而提出的，具有重要的意义。其实在解决生活中的困难时，难免遇到问题，而遇到问题则是数学家们展开研究的动机，这样的问题同样也可以成为学生研究和学习的动机。

与此同时，教师也可以布置一项让学生观察日常生活中的函数关系的作业，如家里的水费和电费是按照什么样的规则计算的，是否可以写成函数关系？坐出租车时，司机是按照什么样的规则计价收费的，是否也可以写成函数关系？下次上课时，教师可以组织学生对生活中的函数关系进行交流讨论，说明自己得出函数关系的过程，应用了哪些知识，让数学概念回归于生活，同时培养学生举一反三的能力。

结语

生成性教学已逐渐成为现代教育研究的一个热门话题。数学概念作为数学的细胞，如何进行数学概念的生成性教学，如何更好地捕捉课堂上的生成性资源，如何促进数学概念的有效生成，已成为一线数学教师关注的焦点。因此，生成性教学无论是在数学概念的教学中，抑或是在其他方面的教学中，都值得推广和应用，促进学生有效学习，提高教学质量。

参考文献：

[1]余国良.生成性教学：概念、特征与路向[J].教育实践与研究，2019（4）：49.

[2]吕荣平.高一物理概念生成性教学设计策略研究[D].兰州：西北师范大学，2017.

[3]顾晓莉.利用数学史开展生成性教学——以复数概念的教学为例[J].中学数学，2019（15）：2425.

[4]任建文.高中数学概念生成过程“问题链”式教学设计研究[J].数学教学通讯，2017（21）：1516.

责任编辑：唐丹丹