基于学习路径分析的小学数学单元整体教学策略研究

摘要：理解数学原理与掌握运算方法是提升运算能力的两个关键，其目的是实现两者间的有效结合。在学习多位数乘法时，“两位数乘以两位数”成为核心学习环节，其教学的重点在于加深对此算数原理的理解和掌握相关的算法。基于此，通过文献分析法与案例分析法，分析小学数学单元整体教学路径。研究发现，系统的学习路径规划能够显著提升学生的数学学习兴趣，优化学习环境，从而有效提高学生的学习成绩与自我效能感。

关键词：学习路径；小学数学；单元整体教学；两位数乘两位数

中图分类号：G623.5""文献标识码：A""文章编号：1673-8918（2024）48-0066-04

《义务教育数学课程标准（2022年版）》中指出：“运算能力主要是指根据法则和运算律进行正确运算的能力。”运算能力是学生数学核心素养的重要组成部分，其也是数学教师开展人才培养工作的主要目标。小学数学教师要认识到以单元整体教学为基础培养学生运算能力的重要性和必要性，并结合小学生的个性特点和认知基础，针对性采用符合小学生兴趣偏好的多元化教学手段，辅助学生在兴趣驱动下形成完整的知识架构和突出的运算能力。文章以人教版《两位数乘两位数》这一单元为例，深度分析了小学数学教师开展单元教学活动的策略，明确教师在单元教学中要构建可达成的教学目标，并深度分析单元内容，确保所设计的教学计划能够促进学生核心素养的发展和提高。

一、理解单元学习目标

（一）单元教学内容概述

人教版《数学》教材作为广泛使用的教学资源，其内容的编排和学习目标的设定均经过精心设计，旨在促进学生全面而深入地理解和应用数学知识。在此背景下，三年级上册第四单元“两位数乘两位数”单元的学习目标，不仅涵盖具体的计算技能，更强调理解和解决问题的能力。掌握基础的计算方法是学习的基石。学生需学习多种类型的乘法计算，其中包括两位数乘一位数（涉及进位）、两位数乘整十数和整百数（不涉及进位），以及整十数乘几百几十数（不涉及进位）。计算方法的掌握不仅是为能够解决具体的数学题目，更重要的是通过具体的计算练习。学生可理解乘法的本质，掌握乘法的基本规律，从而为更复杂的数学运算打下基础。

两位数乘两位数的计算和理解算理对深化数学理解具有突出意义。通过具体的计算实践，学生不仅可体验到解决问题的过程，更能在实践中探索和理解乘法的算理，如乘法的分配律、结合律等。对算理的理解，不仅能帮助学生更加准确无误地完成计算任务，还能在学生的心智中构建数学概念的框架，促进数学思维的发展。

（二）确定核心目标

本单元作为“数与代数”领域中“数与运算”主题的一部分，着重强调对学生运算能力的系统培养。在数学教育中，算理理解与算法掌握被视为运算教学的“双翼”，二者紧密相连，构成教学的有机整体。良好的运算能力不仅体现在对算法原理的深刻理解上，更体现在能够熟练运用算法解决问题的能力上。学习“两位数乘两位数”，作为整数笔算乘法教学的关键环节，标志着学生在数学学习路径上的重要跃进。该单元的教学，让学生首次面对较为复杂的分层次记录方式，不仅是技能上的挑战，更是对学生逻辑思维和理解能力的考验。在此过程中，学生需学会如何按顺序进行乘法操作，并且能够理解并运用分层记录的原理。同时，准确地标记各个部分的乘积位置，对习惯更直接简单运算方式的学生来说，无疑是全新的挑战。

教师在本单元的教学中应当把握两个教学重点：一是深化学生对两位数乘两位数算法理解的广度和深度，二是精确教授并练习竖式运算的标记方法。通过精细化的教学设计，使学生在理解算法的基础上、能够灵活运用算法，进而提升其解决复杂问题的能力。因此，在本单元的教学中，教师需着眼于对“两位数乘两位数”的算理理解和竖式运算记录的教学，旨在通过算理的深刻理解来促进算法的熟练掌握。在本教学单元的设计中，教师应将重点放在深化学生对“两位数乘以两位数”数学概念的透彻理解上，并强化其使用竖式计算法的技能掌握。这一教学策略的关键在于深度剖析乘法运算的内在逻辑与基本规则，可以为学生搭建一个稳固的知识框架，从而能够灵活且精确地运用竖式方法解决两位数相乘的实际问题。

（三）核心目标具体化

基于上述核心目标的确立，将核心目标具体化为理解算理和掌握竖式记录方法的两个关键点，教师可更精确地指导教学活动的设计和实施，确保教学内容既有深度又有广度。理解两位数乘两位数的算理，不仅局限于掌握计算过程，而且要求学生深入理解乘法的数学本质，其中涵盖数的分解与重组、乘法的分配律等基础数学原理。该目标的实现分为四个层次，即从理解两位数结构和乘法算式的基本意义出发，到能够独立运用计算方法并说明其合理性；进一步能够理解并比较不同的计算方法，最终能够在对不同方法的理解和比较基础上，从而提炼并掌握更为通用的计算法则。此过程涉及的不仅是算法技能的提升，更重要的是通过对算理的深入理解，促进学生的逻辑思维和数学抽象能力的发展。

掌握两位数乘两位数竖式记录方法是学习路径中的另一核心目标，不仅要求学生能够准确无误地进行计算，更要求其理解竖式计算的每一步骤所代表的数学意义，包括每一位数字的位置价值以及乘法和加法运算的嵌套关系。学生需通过具体的计算实践，感受竖式记录与实际计算过程的紧密联系，理解每一个运算步骤的逻辑基础，从而建立完整的算法模型。在此过程中，教师需通过设计具有挑战性和趣味性的问题情境，引导学生主动探索、比较不同的解题策略，最终形成对竖式算法深刻的理解和熟练的应用能力。

二、确定学习起点

（一）学生的算理理解水平分析

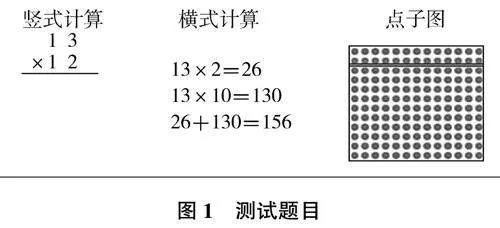
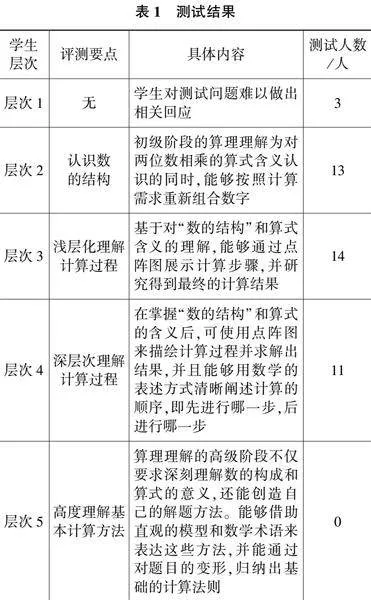
为准确把握学生对算理的理解程度，文章研究依托算理理解的四个层次，设计评估“两位数乘两位数”笔算理解的表现性评价框架，并进行初步测试。测试题目要求学生思考“13×12”的含义及其计算方法，同时用横式记录自己的解题过程，并尝试使用点阵图来展现解题步骤。测试结果如表1所示。

初步测试结果显示，大部分学生可理解乘法算式的本质并重新排列数字。超过半数的学生能通过绘制分点阵图和采用个人解题策略正确求解13×12的结果。然而，部分学生在使用数学语言描述计算步骤时遇到困难，难以明确指出计算的先后顺序，也未能自主地从复杂的解题方法中简化并抽象出基础算法。

（二）学生的竖式记录情况分析

为准确掌握学生在竖式记录方面的实际表现，同样也进行预测试。测试题目如图1所示。

从预测试的数据分析中得知，共有19名学生未能正确完成乘法竖式的书写，表明竖式记录对其而言具有一定难度。另外，对成功书写出正确竖式的22名学生，通过进一步访谈发现，其中有6名学生难以将竖式、横式和点阵图相互关联，对竖式的理解主要依赖于记忆和模仿。因此，为加深学生对竖式的理解，教师需要指导学生体验从横式到竖式的转变过程，并明确横式、竖式与图示之间的内在联系，实现算理与算法的有效融合，进而帮助学生构建完整的算法理解模型。

三、单元整体设计分析

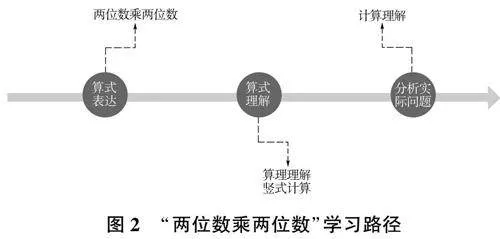
依据人教版《数学》的知识结构，“两位数乘两位数”的学习内容被划分为三个主要阶段：学生接触与掌握基础的口算乘法；学生进入两位数相乘的笔算学习，从不涉及进位的笔算开始，逐步过渡到涉及进位的复杂笔算；学生学习通过连续乘法和除法的两步计算方法来解决实际问题。对学生学习情况进行分析后发现，学生在理解“两位数乘两位数”的笔算原理及竖式记录方面遇到不同程度的挑战。因此，在笔算的教学过程中，教师应根据学生对算理的理解程度，引导其深化对算理的理解。同时，教师需有效链接实际情境、计算过程以及竖式记录的学习路径，以构建算法模型的深度理解，如图2所示。

基于上述分析，对“两位数乘两位数”单元的教学内容进行以下调整：

首先，针对“6×10”这一知识点的处理方式，建议避免直接将其作为新课讲授，鉴于学生已扎实掌握“六十即六个十”的快速计算基础，可以探索如“6×9后加6”的算法介绍。尽管该方法有其实际应用背景，但易与学生既有认知发生冲突，影响知识体系的稳定性。建议仅在复习阶段提及6×10，通过强化训练巩固这一简便算法，同时凸显一位数乘以10的效率优势；进一步地，采用“12×10”为切入点，引入并深化两位数乘以整十数的概念，作为教学核心。

其次，将“两位数乘两位数的笔算”设定为深化理解多位数乘法原理与技巧的核心教学环节。鉴于算理理解对算法掌握的根本性作用，教学中应强化算理教育的重要性。建议将此教学内容分散至连续两课时，第一课时聚焦算理的透彻剖析，帮助学生构建坚实的理论基础；第二课时则侧重竖式计算的实践操作，确保学生能够准确地将理论转化为技能。此教学设计跳出了传统教材中“无进位”与“有进位”的机械划分，转而从算理领悟与竖式规范书写的角度出发，更加契合学生的认知成长轨迹。通过连续的课程设置，不仅促进了学生对算理与算法的综合掌握，还维护了思维活动的连贯性和系统性。

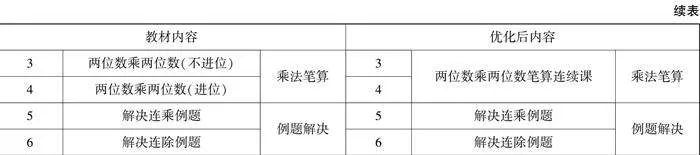
在教学策略上，对整个“两位数乘两位数”单元，教师可灵活调整教学序列，如表2所示，以更加符合学生认知发展规律的方式组织教学活动，促进学生由浅入深、循序渐进地掌握乘法运算的核心知识与技能。

本调整方案将教学内容主要分为乘法口算、乘法笔算和例题解决三部分，其中乘法笔算的学习阶段接受显著的调整，以更好符合学生的认知发展需求。

乘法口算阶段，教学的目标是使学生熟悉并掌握基础的乘法口算技巧，包括对简单乘法算式的快速计算能力。通过各种教学活动和练习，学生可加深对乘法运算规则的理解，为后续更复杂的笔算乘法打下坚实的基础。此阶段的教学，虽然看似简单，但对培养学生的计算速度和准确性至关重要，也有助于提升学生对乘法运算的直觉理解。

乘法笔算阶段是本单元的核心，调整更为明显。原本教材中按照是否进位将两位数乘两位数的笔算分为两部分教学。此方法虽然在逻辑上有其合理性，但在实际教学中很难完全符合学生的认知规律。调整后，该阶段被设计为连续的两节课，更加注重算理的理解和竖式计算技能的培养。在第一节课中，教师没有立即引入竖式的具体计算方法，而是通过实际例子和情景模拟，帮助学生理解乘法算理的不同层次。此教学方法旨在使学生能够在没有形式化算法的情况下，通过逻辑推理和现实情境的联系，理解乘法运算的本质；而第二节课则专注于竖式计算方法的教学。在此环节中，教师引导学生逐步理解并练习两位数乘两位数的竖式计算过程，强调竖式记录的逻辑性和系统性。通过将竖式计算与具体的生活情境相联系，教师帮助学生理解竖式计算每一步骤的意义，让学生总结数学运算不是孤立的技巧，而是与现实世界紧密相关的逻辑过程。

例题解决阶段是将之前学习的知识应用于实际问题中，通过解决具体的数学题目，学生可以巩固和深化对乘法口算和笔算的理解。在此阶段，教师通过引入多样化的题型，旨在训练学生的问题解决能力和创新思维。通过挑战不同难度的题目，学生能够在实践中掌握如何灵活运用乘法算法解决问题，进一步提高自己的数学思维能力。

四、结论

综上所述，在“两位数乘两位数”的教学中，学习路径分析不仅为教师提供有效的工具来识别和解决学生学习过程中的具体问题，也为学生提供更加个性化和高效的学习方案。此方法的应用，无疑将促进小学数学教学由传统的“一刀切”模式转向更加灵活、多元和精准的方向发展，进而实现教与学的高度匹配和深度融合。未来，小学数学教学需更加重视学习路径的多样性和灵活性，以适应每个学生独特的学习需求和能力。

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022.

［2］刘小兵.基于“学习路径”的单元整体教学探索［J］.数学教学通讯，2023（1）：27-28.

［3］苏国冬.基于学习能力提升的小学数学单元整体教学路径研究［J］.教师，2024（3）：39-41.

［4］汪东兴.基于学习路径视角的小学数学单元整体教学研究——以“多边形的面积”一课为例［J］.甘肃教育，2022（11）：108-114.

［5］黄朝鹏，黄山，潘婉婷.基于学习路径分析的“厘米和米”单元整体教学［J］.教师博览，2023（6）：92-94.

［6］章勤琼，陈锡成.基于学习路径分析的小学数学单元整体教学思考框架［J］.小学教学，2021（6）：13-16.

［7］阳海林，陈怡璇，章勤琼.基于学习路径分析的项目式学习单元整体教学［J］.教学月刊（小学版），2024（2）：83-86.

［8］滕艳艳，章勤琼，厉梦妮.基于学习路径分析的“混合运算”单元整体教学——明确学生基础顺学而教［J］.教学月刊（小学版）数学，2022（4）：55-58.

课题项目：文章系广东省中山市重点课题“基于学习路径分析的小学‘数与运算’主题单元整体教学研究”（课题编号：A2022018）研究成果。

作者简介：黄慧霞（1983～），女，汉族，广东江门人，广东省中山市阜沙镇丰联小学，研究方向：小学数学单元整体教学。