高中数学建模素养培养案例分析

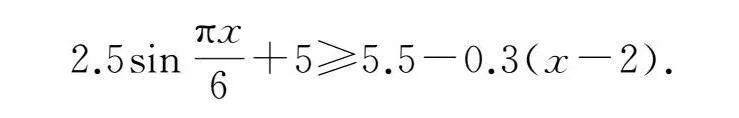
摘要：通过建模将实际问题转化为数学问题，进而利用数学知识解决问题，用模型解释现实生活中与数学知识有关的现象与规律.本文中以“三角函数的应用”为例，详细分析了数学建模的过程，旨在促进学生数学建模素养的培养.

关键词：新课标；高中数学；建模素养；培养案例

新课标背景下高中数学建模素养的培养越来越受到重视.本文中以“三角函数模型简单应用”的一个实际教学案例为例，展示如何引导学生在分析问题、解决问题的过程中培养学生的数学建模素养.

1 呈现实际情境，激发建模意识

在“三角函数的应用”这一课教学中，课程目标要求学生能够运用已知的三角函数模型解决实际问题，可以将具体周期变化规律的实际问题抽象为三角函数模型，并使用三角函数模型解决一些实际问题[1].学生通过选择问题、构建及求解数学模型，再到实际问题的解决，经历了数学建模全过程，综合考虑了实际问题特点和函数模型间存在的内在关联性，充分感受到三角函数在日常生活中普遍存在，更加深刻地认识到三角函数在生活中的功能性，促进数学知识应用意识的提升.整堂课涉及到的知识点较多，如果仅仅依赖课堂枯燥乏味的讲解，学生很难掌握重难点，建模意识的激发更是无从谈起.针对此种情况，笔者认为可以通过问题情境的创设、三角函数知识点清晰呈现，以及一系列问题的提出，引导学生思考，逐渐形成建模意识.通过精心设计“三角函数的应用”教学各个环节，笔者结合学情给出了以下问题：

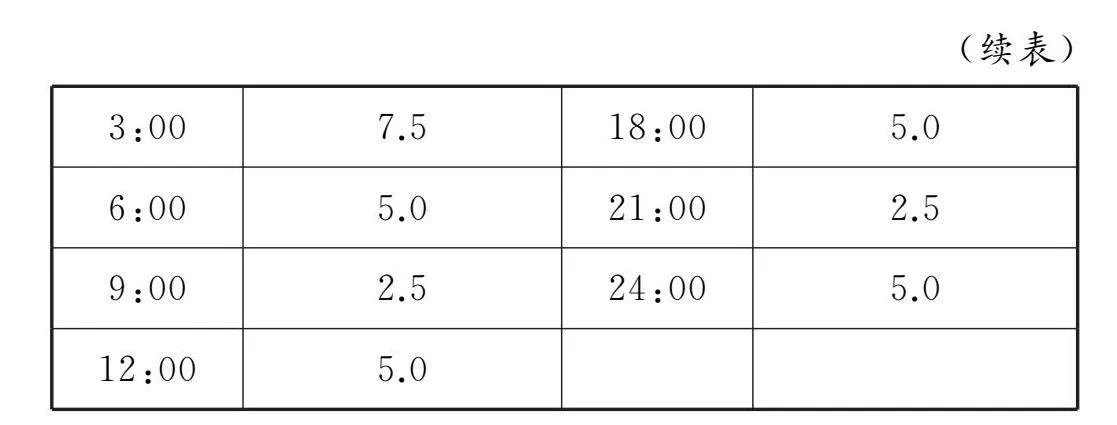
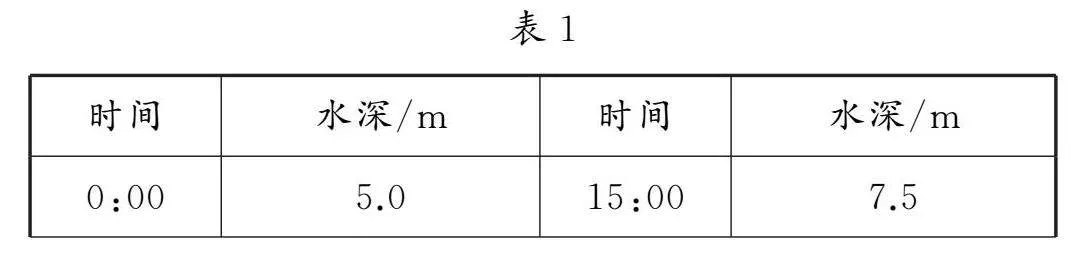
在日月引力的影响下，海水会出现涨落现象，这一现象被称之为潮，早潮叫作潮，而晚潮则称为汐.通常情况下船只会在涨潮的时候驶入航道，向码头靠近；将货物卸完以后，又会在落潮的时候快速返回海洋.某港口某季节每天几个时刻的水深见表1.

根据表1分析以下问题：

（1）选择一个函数近似描述此港口水深和时间函数间的关联性，同时求出整点时间水深近似值（精确到0.1 m）.

（2）如果某船吃水深度是4 m，安间间隙是1.5 m，2：00卸货，吃水深度减少的速度是0.3 m/h，此时船何时能进入港口？何时必须要停止卸货，驶向深水域？

通过以上问题情境的呈现，以此为主线进行探究，层层递进，其中问题（1）引导学生初步感受现实生活中呈周期变化的三角函数问题，运用三角函数模型求解实际问题；问题（2）则鼓励学生在自主分析实际问题的同时，构建三角函数模型，并解决实际问题，加深对三角函数与实际生活的关联体验，掌握数学建模的完整步骤与方法.学生在体会数学思想的过程中，建模意识逐渐增强，数学素养有所提升.

2 正确理解实际问题，建立数学模型

2.1 小组合作，获得水深与时间关系函数模型

在探讨问题（1）时，笔者认为可以先要求学生仔细观察表1中数据的变化，从中获取相应信息，鼓励小组间进行合作探讨，然后由代表发言.在各小组深入讨论以后，有的小组得出以下结果：水深最大值7.5 m，最小值2.5 m.也有的小组得出结果：水的深度由5.0 m增加至7.5 m以后慢慢开始减少，直至减少到2.5 m，又开始变深，增加至7.5 m以后，开始减少.最后教师总结，水深变化呈现一种周期性规律.为了能够使学生更加清晰地看到数据变化的规律，笔者认为可以给予学生更多主动权，积极开展动手活动，鼓励学生通过作图的形式将这种变化呈现出来，以更加直观明了地看到周期性变化规律.在此基础之上，还可进一步总结作图结果，提出更加深入的问题：“与之前学过的哪个函数类型类似？”紧接着提问：“为什么与正弦型函数y=Asin（ωx+φ）类似（采用的是排除法，关注的是周期性）.新旧知识相结合，让学生求解.学生选用函数y=Asin（ωx+φ）+h（A＞0，ω＞0）描述水深与时间的关联性，结合表1的信息求出A=2.5，h=5，T=12，φ=0，ω=π6，所以

y=2.5sinπx6+5.

得出刻画水深与时间关系的三角函数模型后，为保证选择的函数更加精准，笔者认为鼓励学生进行检验也是非常有必要的.此时可提出建模过程——选模、求模、验模、应用，在此模型基础之上，让学生以小组为单位探讨：“通过此模型大致可以知道水深与时间关系的哪些情况？”学生思考与探讨以后做出如下回答：如周期、单调性、每时每刻的水深.在学生将几个值计算出来后，教师展示水深与整点时间数值表.整个过程突出小组间的合作与探讨，利于帮助学生获取更多的知识点，准确获取水深与时间关系函数模型[2].

2.2 强化跨学科建模思想，培养创造迁移能力

新课标要求重视学生数学核心素养的培养，促进思维品质以及数学能力的提升.在数学教学环节中渗透建模思想，对于学生实践能力的培养非常有利[3].

笔者认为在讲解货船安全深度未变这一知识点时，可以进一步呈现货船载满货物进入港口这一内容，并与物理学科知识点有效结合提出问题：卸货时船身逐渐减轻，船身上浮，同时吃水深度均发生变化，此时如何选择进出港时间？此问题提出以后，引导学生探究问题（2）.学生在经过讨论后得出：实际水深≥安全水深，即

2.5sinπx6+5≥5.5－0.3（x－2）.

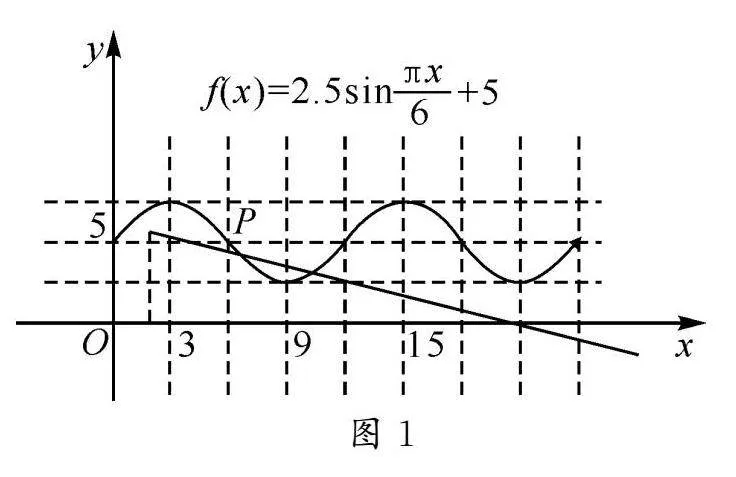
在探讨以后选择运用几何法求解，并利用几何画板作图进行呈现，如图1所示.学生借助图象便可直观看到：即将到达p时刻时，货船需要停止卸货，向深水区驶去，如何求解点P的坐标呢？学生思考、讨论求出点P的横坐标.

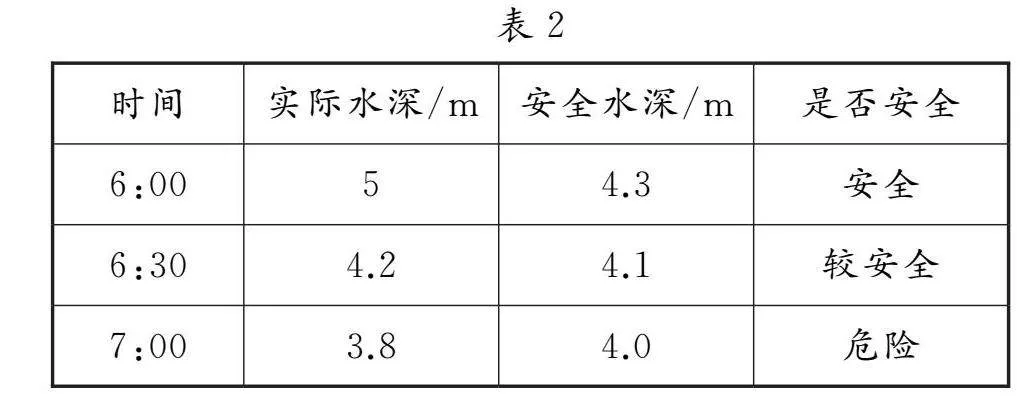
或采用数形结合法、二分法求得近似解.根据图形可获得点P的横坐标在区间［6，7］内，因此仅需将6：00，6：30，7：00这3个时间点安全水深和实际水深值（见表2）计算出来，就可以解答问题.

结合以上分析，为了进一步培养学生的创造力，笔者提出问题“若时间控制不合理，货船便会发生未卸完货就要暂时离港，待水位上涨以后方能驶回继续卸货的情况，无形之中浪费了人力、财力”，鼓励学生探讨如何解决此问题.学生得出结论：卸货时间加快，换言之加快安全深度降低的速度.建模的时候通过数学语言构建了数学与其他学科间的关系，突破了三角函数的重难点，使学生站在物理视角解决数学问题，同时基于数学视角了解物理知识，促进了创新迁移能力的提升.而拓展性问题的提出，给予了学生更多想象的空间，基于现有数学模型，结合所学三角函数知识，根据生活经验解决现实生活中的实际问题，实现了数学知识的再创造与迁移.

高中数学教学过程中涉及到的各知识点具有较强的逻辑性、实践性[4]，要想使学生全面且系统化地掌握这些知识点，笔者认为这就需要在讲解基础知识的同时，借助数学建模活动的开展，给予学生正确引导，通过数学建模思想快速解决问题，在促进学生建模意识形成的过程中，便可以系统化梳理知识结构，促进建模素养的培养.这样，数学学习效果会更加理想.

参考文献：

[1]李佳香.新课程新教材对高中数学教学中数学建模的启发[J].数理天地：高中版，2023（17）：59-61.

[2]马利雅.谈新课标下高中生数学建模能力的培养策略[J].中文科技期刊数据库（引文版）教育科学，2023（5）：185-189.

[3]彭介顾.新课程标准下的高中数学建模教学实践研究[J].数学学习与研究，2022（17）：125-127.

[4]袁慧春.新课标背景下高中数学教学中培育学生建模意识的方法[J].天津教育，2023（11）：104-106.