基于核心素养的高三数学复习课单元教学设计策略

摘要：高三作为高中数学学习的特殊阶段，为学生核心素养、思维能力的培养提供了难得的机会.怎样在高三数学复习课中改变相对固化的试题形式、减少死记硬背和机械刷题，以适应高考改革中重视学科知识本质与通性通法的要求呢？本文认为应居高临下，采用单元教学，从整体上把握教学内容，优化整合知识点.由此提出了基于核心素养的高三数学复习课单元教学设计的四条策略，即站在学科高度、聚焦核心知识、思考知识本质、感悟解题思想，并结合“向量”单元予以实施.

关键词：核心素养；高三数学复习课；单元教学设计；策略；向量

高考是高中数学教学的“指挥棒”，高考数学命题新趋势以“突出数学本质，重视理性思维，坚持素养导向”为原则[1].面对高考数学命题新趋势，新授课教学方式的改变固然重要，那么作为知识学习的高级阶段的高三数学复习课的教学同样起着至关重要的作用，因此探究高三数学复习课教学是非常有必要的.

在传统高三数学复习课中，教师更多关注的是知识的梳理与解题的技巧，而忽略了知识间的内在联系、数学思想方法的总结与思维的培养.笔者在研读文献[2][3]的基础上，结合自己的实践与思考，提出了基于核心素养的高三数学复习课单元教学设计的四条策略，即站在学科高度、聚焦核心知识、思考知识本质、感悟解题思想，并以高中“向量”单元为例，对这些策略予以实施.

1 站在学科高度

经过高一、高二的数学学习，学生已经完成了知识量的积累，因此高三应站在数学学科高度，整体把握教学内容，居高临下，从横向与纵向上建立知识间的内在联系，实现高中数学知识的深度融合.站在学科高度，符合单元教学设计的理念，有利于实现教学内容的整体化设计和结构化思考，避免了“只见树木不见森林”学习现象.现以高中向量单元为例，站在数学学科高度进行分析.

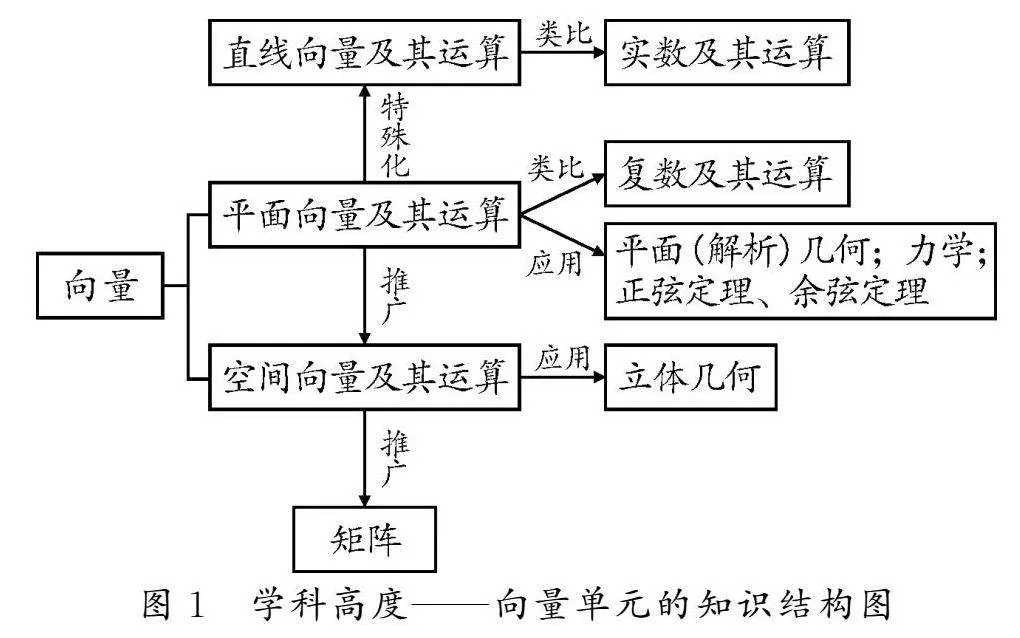
高中向量的学习主要包括平面向量与空间向量.其中平面向量的学习是基础与核心，空间向量是平面向量的推广，即从二维空间到三维空间.有了二维与三维向量，那么有没有其他维度的向量呢？很容易想到共线向量就是一维向量的运算，即直线上的向量，那么多维向量就可以看作是矩阵，这样多维度向量的知识结构就建构完成.

向量是既有大小又有方向的量，大小决定其具有代数意义，方向决定其具有几何意义，所以向量是沟通代数与几何的桥梁.直线上向量的运算及运

算律类比于实数；复数及其运算类比于平面向量的坐标运算；平面向量的线性运算与数量积运算的几何意义应用于解决平面（解析）几何的平行、垂直、长度、夹角等问题；空间向量中借助直线的方向向量与平面的法向量，利用空间向量的坐标运算解决立体几何中线面平行、垂直的证明及线面的距离、夹角等问题，简化了复杂立体几何的证明、计算等问题.这样站在数学学科高度的向量单元的知识结构就建构完成，如图1所示.

几何与代数主线在必修课程中的内容包括：平面向量及其应用、复数、立体几何初步；在选择性必修课程中的内容包括：空间向量、平面解析几何.站在数学学科高度，通过向量单元知识网络的建构，整个“几何与代数”主线的内容就实现了深度融合，建立了知识间的内在联系.因此，站在学科高度是提高学生核心素养的前提.

2 聚焦核心知识

站在数学学科的高度，构建了相关的高中数学知识体系，接下来的复习课单元教学设计不是进行知识点的逐一罗列，而是应突出重点，寻找核心知识点.现以高中“向量”单元为例，聚焦单元核心知识进行分析.

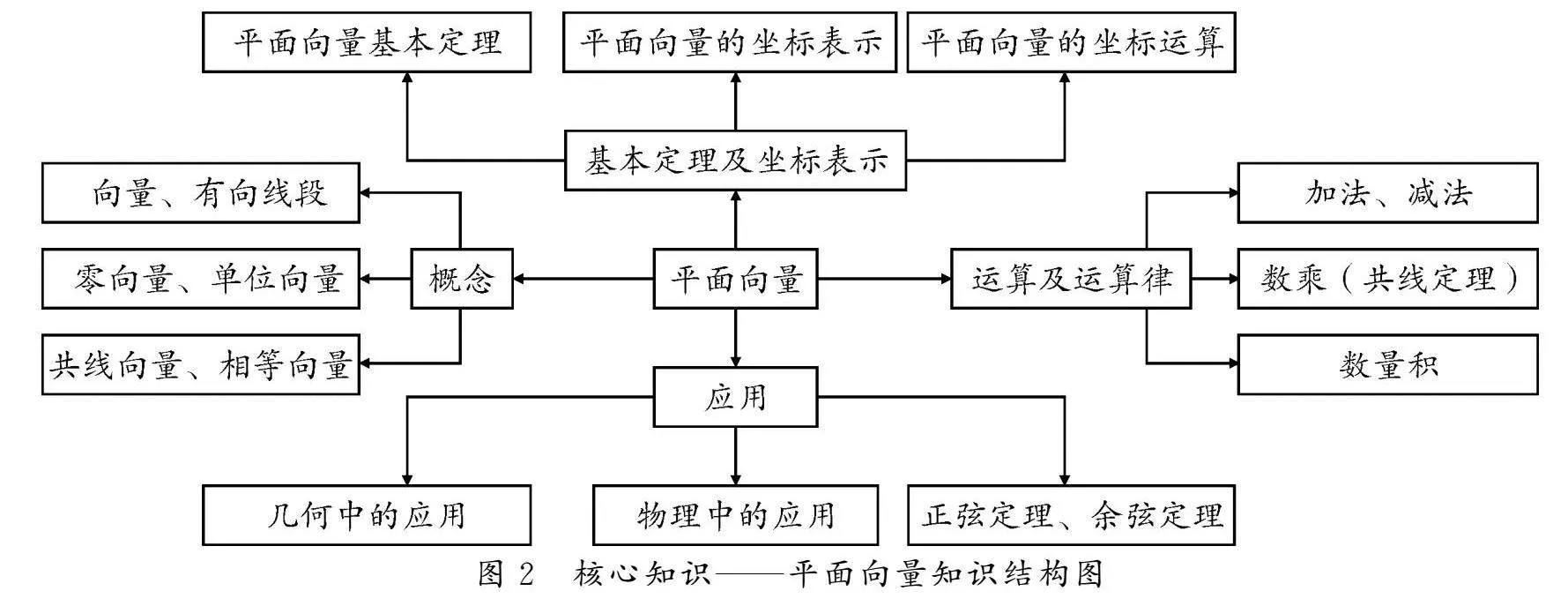
在向量单元的学习中，从内容与数学思想方法上看，平面向量具有基础与核心的地位，主要体现在以下四点：一是类比平面向量，对复数几何意义的理解与复数的运算起到了决定性作用；二是平面向量的推广，从二维的平面向量推广到三维的空间向量，使空间向量的学习易于接受与理解；三是平面向量的特殊化，从二维的平面向量特殊化到一维直线上的向量，直线上的向量及其运算究其本质是实数及其运算；四是利用平面向量的坐标化与数量积运算，沟通了平面解析几何中的平行、垂直、距离、角度等问题.因此，理解与掌握平面向量的内容对向量单元知识的学习起着基础与支撑作用.平面向量单元的具体内容包括：平面向量的概念、运算、基本定理及坐标表示、应用.如图2所示：

2.1 平面向量的概念

首先借助位移、力、速度等物理背景，类比数的概念，得到了向量的概念；类比有向线段，获得了向量的几何表示，帮助学生直观感知与理解“方向”问题.

2.2 平面向量的运算

向量是既有大小又有方向的量，因此向量的运算自然要考虑其大小与方向.类比物理背景中位移的合成，学习了向量加法的三角形法则；类比力的合成，学习了向量加法的的平行四边形法则.类比数的减法“减去一个数等于加上这个数的相反数”，引入了相反向量完成了减法运算.在数的运算中，存在几个相同数相加的情况引入了数的乘法，类比向量中若是几个相同向量相加而引入了向量的数乘运算；从数乘运算的结果发现了向量之间的位置关系，给出了共线定理.学习了向量的加法、减法、数乘运算后，类比数的运算提出问题：向量是否可以相乘？借助物理背景中功的定义，学习了向量的数量积运算，给出了投影向量的含义.在每种运算给出后，进而研究了向量的运算律.这样类比数的运算，向量的运算形成了完整的运算体系.

2.3 平面向量基本定理及坐标表示

结合物理背景中力的分解，由平行四边形法则与向量共线定理的运算，得到了重要的平面向量基本定量.根据平面向量基本定理中两基底位置的特殊化，即两基底互相垂直，建立了平面直角坐标系，完成了向量表示的坐标化，这样向量的运算就化归为实数运算.向量的坐标表示实现后，结合运算体系，完成了向量坐标下的加、减、数乘、数量积的运算.

2.4 平面向量的应用

向量的引入借助了物理知识，因而利用向量可以解决物理中的问题；又因向量具有很强的几何意义，因此在平面几何中有广泛应用；向量的数量积运算涉及到长度与角度，因而可利用向量探索三角形的边角关系，使向量成为证明正弦定理、余弦定理强有力的工具，同时沟通了向量与三角函数的联系.

平面向量作为向量单元的核心知识，理解与掌握其几何意义及其运算，然后通过知识的类比、推广与特殊化等，有利于实现整个向量单元知识的迁移与融合，成为向量单元知识的固着点与生长点.因此，聚焦核心知识是发展核心素养的基础.

3 思考知识本质

俗话说：“透过现象看本质.”数学题是怎么都做不完的，有的学生整日埋头在题海中，机械刷题，焦急疲惫地去记各种结论与技巧.如今高考数学命题新趋势正通过改变相对固化的试题形式，突出数学本质与理性思维，这样高三复习课不应把重点放在刷题上，而应把重点放在对知识的理解上，进行数学知识本质的思考，以不变应万变.现以高中“向量”单元为例，进行知识本质的思考.

例如图3所示，已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等，A1在底面ABC内的射影为△ABC的中心D，求AB1与底面ABC所成角的正弦值.

分析：本题求直线与平面所成的角，有两种方法，即几何法与空间向量法.

几何法：如图4所示，由线面角的定义，直线AP与平面α所成的角为∠PAO.对于本题，首先在几何图形中找到AB1与底面ABC所成角.如图5所示，过点B1作底面ABC的垂线与AD的延长线交于点E（△ABC为正三角形，D为△ABC的中心），则∠B1AE即为AB1与底面ABC所成的角，问题转化为sin∠B1AE=B1EAB1，然后利用几何知识计算线段B1E与AB1的长度.

空间向量法：因为A1D⊥底面ABC，又D为正△ABC的中心，所以AD⊥BC.以D为原点，以CB方向为x轴正方向，AD方向为y轴正方向，DA1方向为z轴正方向，建立如图6所示的空间直角坐标系.写出点B1，A，B，C的坐标，分别求出向量AB1与平面ABC的一个法向量n的坐标，则sin∠B1AE=AB1＼5n|AB1||n|.

思考1比较与分析这两种方法的共性与差异，你有什么发现？

揭示知识本质：无论是几何法还是空间向量法，解题的关键都是要根据定义找到与底面ABC垂直的量，以构造出线面角.几何法需要从点B1出发真实地作出B1E⊥平面ABC；而利用空间向量法只需求出平面ABC的一个法向量n（与底面ABC垂直的向量），由于向量与起点无关，即向量是可以任意平移的，所以不用在乎所求法向量的具体位置，这为解决问题带来了很大的便利.

思考2怎样求解两个平面所成的角？几何法与空间向量法有什么共性与差异？

揭示知识本质：无论是几何法还是空间向量法，解题的关键如图7所示，都是要根据定义，分别找到平面α与平面β的垂直量.几何法要先找到两个平面的交线，从交线上的一点真实地分别在平面α，β内作出l的垂线m与垂线n，即作出二面角的平面角；而利用空间向量法只需分别求出平面α与平面β的一个法向量就可以，由于向量与起点无关，所以不用关心所求法向量的具体位置，这与几何法达到了同样的目的.

思考3怎样求解异面直线所成的角？几何法与空间向量法又有什么共性与差异？

揭示知识本质：几何法是将两条异面直线平移到同一个平面内，构成所求的角；空间向量法由于向量是可以任意平移的，直接利用两条异面直线的方向向量求解就可以.

总结：对于直线与平面所成角、两个平面所成角、异面直线所成角的求解，几何法与空间向量法解决问题的本质是相通的.由于向量与起点无关，即向量是可以任意平移的，所以不用关注空间向量法中所求法向量或方向向量的具体位置，这为解决问题带来了很大的便利.通过思考，我们把握了知识本质，找到了解决线面所成角、面面所成角、异面直线所成角问题的通性通法（空间向量法）.思考知识的本质，可以把知识看穿、看透，一针见血，使数学知识变得深刻起来，提升学生的思维力与核心素养.因此，思考知识本质是发展核心素养的关键.

4 感悟解题思想

弗赖登塔尔曾说过：“没有一种数学思考如当初刚被发现时那样发表出来.一旦问题解决了，思考的程序便会颠倒过来，把火热的思考变成冰冷的美丽.”这就需要教师研读课标、教材，借助数学史等，理清知识的发生与发展过程，挖掘具体知识背后蕴含的数学思想方法，变冰冷的美丽为火热的思考.现以高中“向量”单元为例，进行解题思想的感悟.

平面向量作为向量单元的基础与核心知识，那么对于平面向量的知识我们应具备怎样的思维去解决问题呢？这里需揭开具体知识的表层进行深入的剖析.

首先，对于平面向量的“方向”，教材从向量的几何表示，每一种运算中渗透的几何意义出发，诠释了对向量方向的处理.例如：向量加法的三角形法则、平行四边形法则；向量数乘的共线定理；向量数量积的投影向量；向量的模对应着线段的长度等.因此，在解题时要有向量的几何化解题思想.

其次，平面向量基本定理，即平面内的任一向量都可以由平面内的两个不共线的向量（基底）来表示，渗透了向量基底化解题思想.

再次，平面向量数量积的运算结果为数量，实现了向量运算的数量化，还沟通了与三角函数、长度等的关系.这里体现了向量数量积运算下的数量化解题思想.

最后，向量表示的坐标化，实现了把向量的运算化归为实数运算的伟大跨越，以“数”的运算处理“形”的问题，体现了向量坐标化解题思想.

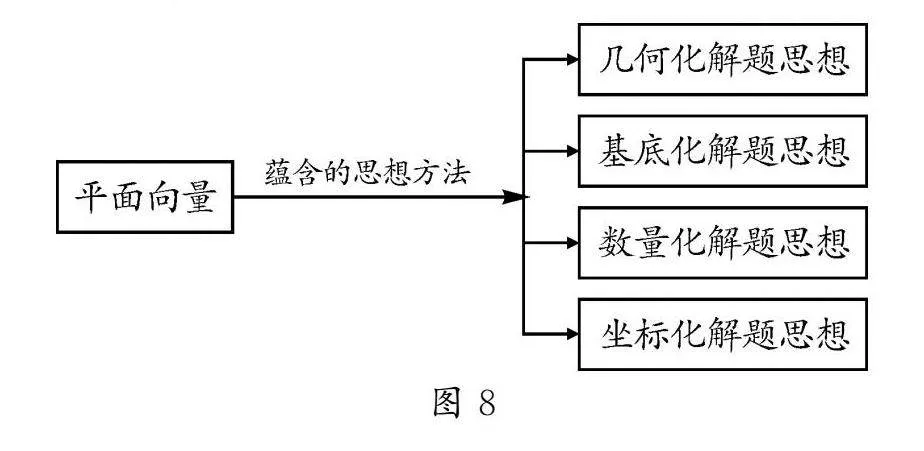
由此可见，平面向量单元蕴含了几何化、数量化、基底化、坐标化解题思想，如图8所示.

通过对平面向量章节具体知识点背后蕴含的解题思想的揭示与感悟，学生在解决平面向量的相关题目时，头脑中将会有解题思想的指导，面对不同问题，将会进行有思想的思考，从而有效地解决问题.因此，感悟解题思想是发展核心素养的核心.

为适应高考数学命题新趋势以及改变传统高三数学复习课教学模式，高三数学复习课应采取单元教学，优化整合知识点，形成系统化与结构化的知识体系，发展学生的思维力，促使数学核心素养落地.高三数学复习课单元教学设计应采取“站在学科高度、聚焦核心知识、思考知识本质、感悟解题思想”的策略，只有这样才能更好地实现高三数学复习课的育人价值.

参考文献：

[1]教育部考试中心.聚焦核心素养 考查关键能力——2021年高考数学全国卷试题评析[J].中国考试，2021（7）：70-76.

[2]李柏青.复习课单元整体教学设计的实践与思考[J].数学通报，2013，52（3）：31-36.

[3]杨林军.宏观 本质 思维——基于能力的高三数学复习策略[J].数学通报，2015，54（12）：24-29.