多角度 拓思维 研一题 通一类

摘要：本文中针对2023年全国甲卷理科第16题，在研究其若干解法的基础上，溯源人教A版新教材，总结求解“爪型”三角形的通法，探究问题的本质以及变式题的编制.

关键词：“爪型”三角形;一题多解;全国甲卷理科第16题

1 真题呈现

（2023年全国甲卷理科第16题）在△ABC中，AB=2，∠BAC=60°，BC=6，D为BC上一点，AD为∠BAC的平分线，则AD=.

2 解法探究

数学家波利亚［1］在《怎样解题》中将解法的思维过程分解为弄清题意、制定计划、执行计划、检验回顾四个步骤，使我们对解题的思维过程看得见，摸得着.针对本题，便可以按照这四个步骤解决问题：

（1）弄清题意：已知三角形的两边及其中一个对角，求已知角的角平分线长.

（2）制定计划：对于解“爪型”三角形的问题，考虑解两个三角形或添加辅助线来求解.

（3）执行计划：实行解决方案，核对每个步骤.

（4）检验回顾：核验答案，总结建模.

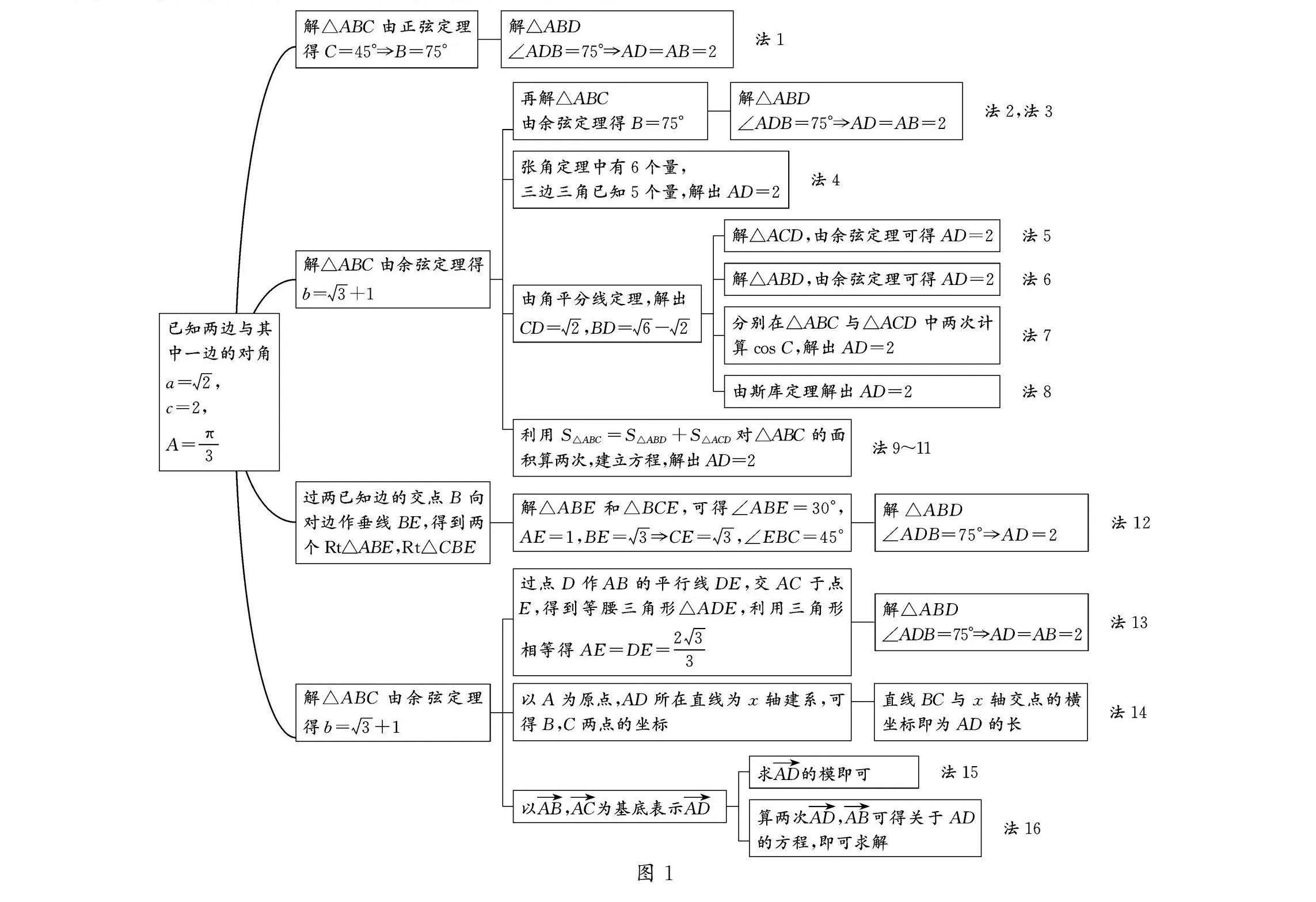
上海市特级教师文卫星［2］老师主张以思维导图的形式对解题思路进行形象总结，此题解法思维导图如图1所示.

已知两边与其中一边的对角a=6，c=2，A=π3

进一步，解△ABC由正弦定理得：C=45°B=75°

第二步，解△ABD，∠ADB=75°AD=AB=2

第一步，解△ABD，∠ADB=75°AD=AB=2

3 试题解析

思路1：角度关系.

解法1：正弦定理.

第①步：在△ABC中，因为AB=2，∠BAC=60°，BC=6，所以

由正弦定理得csin C=asin A，

即2sin C=632=22，

则sin C=22.

又AB<BC，所以C为锐角，因此C=45°，B=75°.

第②步：在△ABD中，∠BAD=30°，∠B=75°，所以∠ADB=75°，即△ABD是等腰三角形.

因此AD=AB=2.

解法2：余弦定理1.

在△ABC中，AB=2，∠BAC=60°，BC=6，由余弦定理有cos ∠BAC=AB2+AC2－BC22AB·AC，

代入可得AC2－2AC－2=0，解得AC=1+3（舍负）.

第①步：在△ABC中，已知AB=2，BC=6，AC=1+3，

所以cos ∠ABC=AB2+BC2－AC22AB·BC=6－24，解得B=75°.

第②步：在△ABD中同解法1，有AD=AB=2.

解法3：余弦定理2.

同解法2，有AC=1+3.

第①步：在△ABC中，已知AB=2，BC=6，AC=1+3，

由cos ∠ACB=AC2+BC2－AB22AC·BC=22，得C=45°，所以B=75°.

第②步：在△ABD中同解法1，有AD=AB=2.

解法4：张角定理.

同解法2，有AC=1+3.

由张角定理可以得到sin ∠BADAC+sin ∠CADAB=sin ∠BACAD，即12AC+12AB=32AD，

所以AD=2.

附张角定理及其证明：

定理内容：如图2所示，在三角形ABC中，D是边BC上一点，∠CAD=α，∠BAD=β，则sin （α+β）AD=sin αAB+sin βAC.

简证：由S△ABC=S△ACD+S△ABD=

12AC·AB＼5sin （α+β）=12AB·ADsin β+12AC·ADsin α，整理即得sin（α+β）AD=sin αAB+sin βAC.

点评：

（1）解法1～3都是通过计算三角形中的不同角度，再利用内角和定理求解三角形.可见，通法之下也有很多变化.解法4的张角定理是初中补充的一个平面几何知识，若知道这个定理可实现秒杀.

（2）解两个三角形是“爪形”三角形问题求解的典型方法.

思路2：长度关系.

解法5：角平分线定理1.

同解法2，有AC=1+3.由角平分线定理可得BDCD=ABAC=23+1，

所以BD+CDCD=3+33+1=3.整理得6CD=3，所以CD=2.

在△CAD中，根据余弦定理可得cos ∠CAD=AC2+AD2－CD22×AC×AD=32，解得AD=2.

解法6：角平分线定理2.

第①步：同解法5，有CD=2，则BD=6－2.

第②步：在△ABD中，由余弦定理得cos ∠BAD=AB2+AD2－BD22×AB×AD=32，解得

AD=2.

解法7：角平分线定理3.

第①步：同解法5，有CD=2.

第②步：在△ACD和△ABC中，由余弦定理有cos C=AC2+CD2－AD22×AC×CD=AC2+BC2－AB22×AC×BC.

解得AD=2.

解法8：斯库顿定理.

第①步：同解法6，有CD=2，BD=6－2.

第②步：由斯库顿定理，得AD2=AB·AC－BD·CD=2（3+1）－2（6－2）=4.

所以AD=2.

附斯库顿定理及其证明：

定理内容：在△ABC中，AD是∠BAC的平分线，则AD2=AB·AC－BD·CD.

证明：如图3所示，作△ABC的外接圆，延长AD交圆于点E，连接CE，

则∠ABD=∠AEC.由角平分线，得∠BAD=∠EAC.

所以△ABD∽△AEC，有ABAD=AEAC.

所以AB·AC=AD·AE=AD·（AD+DE）=AD2+AD·DE.

由相交弦定理有AD·DE=BD·CD，所以AB·AC=AD2+AD·DE=AD2+BD·CD，

所以AD2=AB·AC－BD·CD.得证.

点评：解法5～8都是通过角平分线定理得到两条线段的长度，再使用余弦定理或斯库顿定理，从三角形中的长度关系寻找到目标边长.解题过程中由于选择的三角形不同，运算难度也有所不同，解题时要学会筛选出运算量更小的几何图形.

思路3：面积关系.

解法9：面积法1.

同解法2，有AC=1+3.

第①步：S△ABC=12AB·ACsin 60°=3+32.

第②步：S△ABC=S△ABD+S△ACD=12AB·AD＼5sin 30°+12AC·ADsin 30°=3+34AD.

所以AD=2.

解法10：面积法2.

同解法2，有AC=1+3.

第①步：如图4，过点D作DE⊥AB于点E，过D点作DF⊥AC于点F，设DE=DF=h.

第②步：S△ABC=12AB·AC＼5sin 60°=3+32.

又S△ABC=12（AB+AC）h=3+32h，

所以h=1，则AD=2h=2.

解法11：面积法3.

同解法2，有AC=1+3.

第①步：由角平分线的性质有S△ACDS△ABD=ACAB=3+12，所以S△ACD=3+12S△ABD.

因此S△ABC=S△ABD+S△ACD=3+32S△ABD.

第②步：又因为S△ABC=12AB·ACsin 60°=3+32，所以S△ABD=1.

所以S△ABD=12AB·ADsin 30°=12AD=1.

所以AD=2.

点评：解法9～11都是从面积来入手，由于三角形角平分线模型中蕴含“同高”“等高”的特点，巧用三角形的面积公式，可以直观、快速地建立起边角关系，突破难点.面积法的核心原理是“算两次”，即通过两个不同切入点，依据等面积或面积之比来建立方程求解，这与立体几何中的等体积法的原理相同.计算△ABC面积的不同方法就形成不同的解法.

思路4：平面几何法.

解法12：作垂线.

如图5所示，过点B作AC的垂线交AC于点E.

第①步：在△ABE中，因为∠BAE=60°，∠AEB=90°，所以∠ABE=30°.

又AB=2，所以在直角三角形△ABE中，可得AE=1，BE=3.

第②步：在直角三角形BEC中，BC=6，BE=3，所以EC=3，则

∠CBE=∠ECB=45°.

因此∠ABD=∠ABE+∠EBC=75°，

∠ADB=∠DAC+∠ACD=75°.

所以AD=AB=2.

解法13：作平行线.

如图6所示，过点D作AB的平行线交AC于点E，则∠ADE=∠BAD=∠DAE=30°.

设AE=DE=x.

同解法2，有AC=1+3，则EC=3+1－x.

又△ABC∽△EDC，所以ECED=ACAB，即3+1－xx=3+12，解得x=233.

在△ADE中，DE=233，∠DAE=30°，∠AED=120°，所以

由正弦定理得ADsin 120°=233sin 30°.

所以AD=2.

点评：在平面几何中，作垂线或平行线是常用的添加辅助线的方法.解法12是作垂线，对于已知两边与其中一边对角的解三角形问题，都可以从已知的两边交点出发作高，构造两个直角三角形，再从已知角的直角三角形开始求解，两个直角三角形的边角均可解出.解法13则是添加平行线利用相似三角形求解.

思路5：向量工具.

解法14：坐标法.

同解法2，有AC=1+3.

第①步：如图7所示，以A为坐标原点，AD所在的直线为x轴，建立平面直角坐标系.

由|AB|=2，|AC|=3+1，∠BAD=∠CAD=30°，且点C，B分别在第一、四象限，可得B（3，－1），C3+32，3+12.

第②步：设D（x，0），由BC，BD共线可得1x－3=3+13－1，

解得x=2.

所以AD=2.

解法15：基底法1.

同解法2，有AC=1+3.

第①步：因为AD平分∠BAC交BC于点D，所以

由三角形内角平分线定理有BDCD=ABAC=21+3，

所以BD=23+3BC.

所以AD=AB+BD=AB+23+3BC=AB+23+3（AC-AB）=

23+3AC+1+33+3AB.

第②步：上式两边平方得|AD|2=1（3+3）2＼5［4（1+3）2+4（1+3）2+4（1+3）2］=4.

所以AD=2.

解法16：基底法2.

第①步：同解法15，有BD=23+3BC，所以AD=AB+BD=23+3AC+1+33+3AB.

第②步：又AB·AD=2|AD|cos 30°=3|AD|，

所以AB·AD=AB·23+3AC+1+33+3AB=63=3|AD|，解得|AD|=2.

所以AD=2.

点评：解法14～16通过将几何问题代数化的思路，利用向量作为工具将形和数结合在一起.利用平面向量解决几何问题的两种常用解法为坐标法和基底法.用坐标法解决，关键在于建立恰当的坐标系.用基底法解决，关键在于选择合适的基底向量.

本题的解题思路如图8所示.

4 题目溯源

解“爪型”三角形在近几年的高考试题中曾多次出现，在教材中也存在以中线和角平分线为背景的“爪型”三角形.

溯源1（人教A版标准实验教科书必修5第20页，习题1.2A组第13题）

△ABC的三边分别为a，b，c，边BC，CA，AB上的中线分别记为ma，mb，mc，应用余弦定理证明：

ma=122（b2+c2）－a2，

mb=122（a2+c2）－b2，

mc=122（a2+b2）－c2.

溯源2（人教A版标准实验教科书必修5第19页，习题1.2A组第3题）

如图9，已知一艘船以30 n mile/h的速度往北偏东10°的A岛行驶，计划到达A岛后停留10 min后继续驶往B岛，B岛在A岛的北偏西60°的方向上.船到达C处时是上午10时整，此时测得B岛在北偏西30°的方向，经过20 min到达D处，测得B岛在北偏西45°的方向，如果一切正常的话，此船何时能到达B岛？

5 变式练习

（1）△ABC中，∠BAC=60°，∠BCA=45°，AB=2，∠BAC的角平分线交BC于点D，则BA·BD=.

（2）在△ABC中，∠BAC=120°，AB=2，BC=27，∠BAC的角平分线交BC于点D，则AD=.

参考答案：（1）4－23；（2）43.

参考文献：

［１］波利亚.怎样解题［Ｍ］.徐泓，冯承天，译.上海：上海科技教育出版社，2007.

［2］文卫星.用思维导图解答压轴题——从通法到“秒杀”——以解析几何为例［Ｊ］.中学数学，2021（9）：54-55，63.