2023年新高考全国Ⅱ卷第22题探究

题目

（1）证明：当0<x<1时，x－x2<sin x<x；

（2）已知函数f（x）=cos ax－ln（1－x2），若x=0是f（x）的极大值点，求a的取值范围.

1 试题目标

命题考查点：利用导数证明不等式，已知极值点求参数范围，与三角函数相关的导数.

思想方法：函数与方程思想、数形结合思想、分类与整合思想、化归与转化思想.

能力要求：抽象概括、推理论证.

2 试题来源

本题第（1）问源于新教材选择性必修第二册第97页练习的第1题：

利用函数的单调性，证明下列不等式，并通过函数图象直观验证：sin x<x，x∈（0，π）.

此不等式非常重要，建议学生积累不等式链“sin x<x<tan x，x∈0，π2”，会证明该不等式，并能应用该不等式进行简单放缩.

3 试题分析

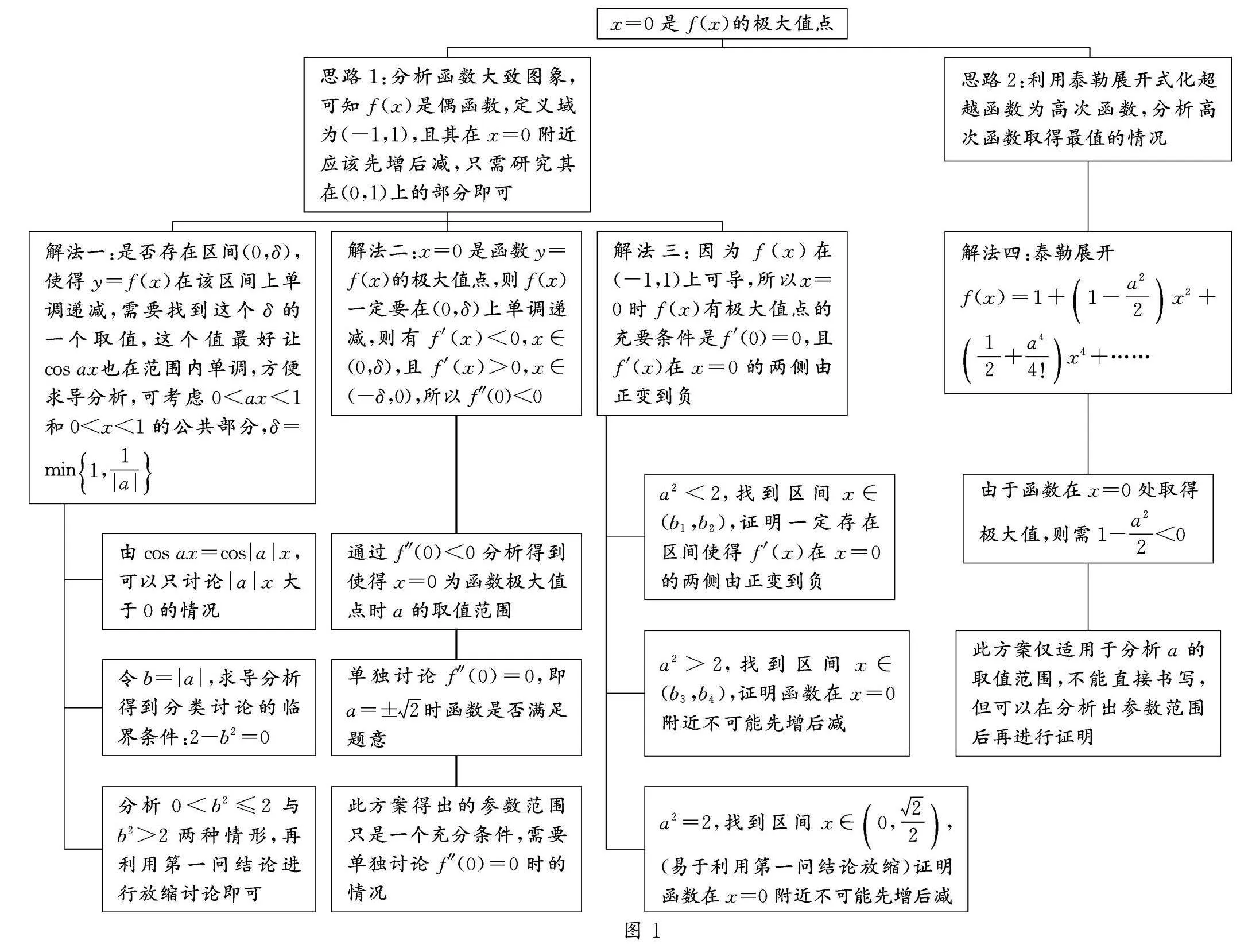
本题的思维导图如图1所示.

x=0是f（x）的极大值点

思路1：分析函数大致图象，可知f（x）是偶函数，定义域为（-1，1），且其在x=0附近应该先增后减，只需研究其在（0，1）上的部分即可

思路2：利用泰勒展开式化超越函数为高次函数，分析高次函数取得最值的情况

解法一：是否存在区间（0，δ），使得y=f（x）在该区间上单调递减，需要找到这个δ的一个取值，这个值最好让cos ax也在范围内单调，方便求导分析，可考虑0＜ax＜1和0＜x＜1的公共部分，δ=min1，1|a|

解法二：x=0是函数y=f（x）的极大值点，则f（x）一定要在（0，δ）上单调递减，则有f′（x）＜0，x∈（0，δ），且f′（x）＞0，x∈（-δ，0），所以f″（0）＜0

解法三：因为f（x）在（-1，1）上可导，所以x=0时f（x）有极大值点的充要条件是f′（0）=0，且f′（x）在x=0的两侧由正变到负

解法四：泰勒展开

f（x）=1+1-a22x2+12+a44！x4+……

由cos ax=cos|a|x，可以只讨论|a|x大于0的情况

通过f″（0）＜0分析得到使得x=0为函数极大值点时a的取值范围

a2＜2，找到区间x∈（b1，b2），证明一定存在区间使得f′（x）在x=0的两侧由正变到负

由于函数在x=0处取得极大值，则需1-a22＜0

令b=|a|，求导分析得到分类讨论的临界条件：2-b2=0

单独讨论f″（0）=0，即a=±2时函数是否满足题意

a2＞2，找到区间x∈（b3，b4），证明函数在x=0附近不可能先增后减

此方案仅适用于分析a的取值范围，不能直接书写，但可以在分析出参数范围后再进行证明

分析0＜b2≤2与b2＞2两种情形，再利用第一问结论进行放缩讨论即可

此方案得出的参数范围只是一个充分条件，需要单独讨论f″（0）=0时的情况

a2=2，找到区间x∈0，22，（易于利用第一问结论放缩）证明函数在x=0附近不可能先增后减

4 解题过程

（1）解析：构建F（x）=x－sin x，x∈（0，1），则F′（x）=1－cos x>0对x∈（0，1）恒成立，则F（x）在（0，1）上单调递增，可得F（x）>F（0）=0，所以可得x>sin x，x∈（0，1）.

构建G（x）=sin x－（x－x2）=x2－x+sin x，x∈（0，1），则G′（x）=2x－1+cos x，x∈（0，1）.

构建g（x）=G′（x），x∈（0，1），则g′（x）=2－sin x>0对x∈（0，1）恒成立，于是g（x）在（0，1）上单调递增，得g（x）>g（0）=0，即G′（x）>0对x∈（0，1）恒成立.于是G（x）在（0，1）上单调递增，可得G（x）>G（0）=0，所以sin x>x－x2，x∈（0，1）.

综上所述：x－x2<sin x<x.

（2）解法一：常规解法.

根据题意结合偶函数的性质可知，只需要研究f（x）在（0，1）上的单调性，求导，分类讨论0<a2<2和a2≥2，结合（1）中的结论放缩，根据极大值的定义分析求解.令1－x2>0，得－1<x<1，即函数f（x）的定义域为（－1，1）.若a=0，则f（x）=1－ln（1－x2），x∈（－1，1）.因为y=－ln u在定义域内单调递减，u=1－x2在（－1，0）上单调递增，在（0，1）上单调递减，则f（x）=1－ln（1－x2）在（－1，0）上单调递减，在（0，1）上单调递增，所以x=0是f（x）的极小值点，不合题意.故a≠0.

当a≠0时，令b=|a|>0，可以缩小讨论范围，且方便利用第（1）问结论进行放缩.

因为f（x）=cos ax－ln（1－x2）=cos（|a|x）－ln（1－x2）=cos bx－ln（1－x2），且

f（－x）=cos（－bx）－ln ［1－（－x）2］=cos bx－ln（1－x2）=f（x）.

所以函数f（x）在定义域内为偶函数，换元后函数仍是偶函数，此处给出简单证明.

由题意，可得f′（x）=－bsin bx－2xx2－1，x∈（－1，1）.

由f′（x）=－bsin bx－2xx2－1>－b2x－2xx2－1=x（b2x2+2－b2）1－x2，发现2－b2≥0时导函数恒大于零，所以可以以此为分析依据对参数进行讨论，之后就顺理成章了.

（ⅰ）当0<b2≤2时，取m=min1b，1，x∈（0，m），则bx∈（0，1），由（1）可得f′（x）=－bsin bx－2xx2－1>－b2x－2xx2－1=x（b2x2+2－b2）1－x2.

又b2x2>0，2－b2≥0，1－x2>0，所以f′（x）>x（b2x2+2－b2）1－x2>0，即当x∈（0，m）（0，1）时，f′（x）>0，则f（x）在（0，m）上单调递增.结合偶函数的对称性可知，f（x）在（－m，0）上单调递减.故x=0是f（x）的极小值点，不合题意.

（ⅱ）当b2>2时，取x∈0，1b（0，1），则bx∈（0，1）.

结合（1），可得f′（x）=－bsin bx－2xx2－1<－b（bx－b2x2）－2xx2－1=x1－x2（－b3x3+b2x2+b3x+2－b2）.

构建h（x）=－b3x3+b2x2+b3x+2－b2，x∈0，1b，则有h′（x）=－3b3x2+2b2x+b3，x∈0，1b，且h′（0）=b3>0，h′1b=b3－b>0，可知h′（x）>0对x∈0，1b恒成立，所以h（x）在0，1b上单调递增.又h（0）=2－b2<0，h1b=2>0，所以h（x）在0，1b内存在唯一的零点n∈0，1b.当x∈（0，n）时，则h（x）<0，且x>0，1－x2>0，则f′（x）<x1－x2（－b3x3+b2x2+b3x+2－b2）<0，即当x∈（0，n）（0，1）时，f′（x）<0，则f（x）在（0，n）上单调递减.结合偶函数的对称性可知，f（x）在（－n，0）上单调递增.所以x=0是f（x）的极大值点，符合题意.

综上，当b2>2，即a2>2，亦即a>2或a<－2时，符合题意.

故a的取值范围为（－∞，－2）∪（2，+∞）.

解法二：极值的第二充分条件.

由f′（x）=－asin ax+11－x－11+x，

f″（x）=－a2cos ax+1（1－x）2+1（1+x）2，

可得f′（0）=0，f″（0）=－a2+2.所以当a2<2时，f″（0）>0，此时x=0不是f（x）的极大值点；当a2>2，即a>2或a<－2时，f″（0）<0，此时x=0是f（x）的极大值点.这里令f″（0）=－a2+2<0，解出参数的范围，此仅为充分条件，仍需讨论f″（0）=0时的参数取值是否成立.

若a=±2，则f′（x）=－2sin 2x+2x1－x2.当0<x<22时，f′（x）>－2·2x+2x=0，注意到f′（x）是奇函数，所以－22<x<0时f′（x）<0.所以a=±2时，x=0是f（x）的极小值点.

此处利用第（1）问的结论“x>sin x，x∈（0，1）”进行放缩，容易发现不合题意.

综上，a的取值范围为（－∞，－2）∪（2，+∞）.

极值的第二充分条件：若x0∈［a，b］，f′（x0）=0，且f″（x0）≠0，则f″（x0）<0时，y=f（x）在x0处取得极大值，f″（x0）>0时，y=f（x）在x0处取得极小值.

证明：

若f″（x0）<0，则有

limx→x0f′（x）－f′（x0）x－x0=limx→x0f′（x）x－x0<0，

即δ>0，当x∈（x0－δ，x0+δ）时，f′（x）x－x0<0.

因此当x<x0时，f′（x）>0，当x>x0时，f′（x）<0.

故f（x）在x=x0取得极大值.

同理可证f″（x0）>0的情形.证毕.

解法三：分析导函数在极值点两侧的正负变化情况.

因为f（x）在（－1，1）上可导，所以x=0是f（x）有极大值点的充要条件是f′（0）=0，且f′（x）在x=0的两侧由正变到负.由f′（x）=－asin ax+11－x－11+x，f″（x）=－a2cos ax+1（1－x）2+1（1+x）2，

可得f′（0）=0，f″（0）=－a2+2.

当a2<2时，f″（0）>0，所以存在区间（b1，b2）（－1，1）（b1<0<b2），有f″（x）>0，x∈（b1，b2）.

所以在区间（b1，b2）上f′（x）单调递增.又因为f′（0）=0，所以f′（x）在（b1，b2）上由负变到正，故a2<2不符合题意.

当a2>2时，f″（0）<0，所以存在区间（b3，b4）（－1，1）（b3<0<b4），有f″（x）<0，x∈（b3，b4）.

所以在区间（b3，b4）上f′（x）单调递减.又因为f′（0）=0，所以f′（x）在（b3，b4）上由正变到负，故a2>2满足题意.

当a2=2时，取区间D=0，22（0，1），由第（1）问可知，当x∈D时，sin2x<2x，所以－2×sin2x>－2x，故f′（x）>－2x+2x1－x2=2x31－x2>0，x∈D，即f′（x）在x=0的右侧为正，不符合题意，所以a2=2不符合题意.

综上，a的取值范围为（－∞，－2）∪（2，+∞）.

解法四：泰勒展开式.

由泰勒展开式，可得

cos ax=1－（ax）22！+（ax）44！-……，

ln（1－x2）=－x2－x42+……，

则f（x）=cos ax－ln（1－x2）=1+1－a22x2+12+a44！x4+…….由于x=0为极大值且f（0）=1，则需1－a22<0，解得a<－2或a>2.

泰勒展开式在局部分析时功效显著，而极值恰好就是一个局部特征.

此方案仅适用于分析a的取值范围，不能直接书写，可以用此方法推断出参数范围后再进行证明.

若学生具备凹凸函数、泰勒展开式等高等数学的知识，解答此类题目会较为容易.这也给我们今后的中学数学教学带来了一些启示，教学中可以适当补充一些《数学分析》的知识，以应对难度日益增加的高考.

5 试题拓展

（Ⅰ）（2018全国卷Ⅲ第21题）已知函数f（x）=（2+x+ax2）ln（1+x）-2x.

（1）若a=0，证明：当-1＜x＜0时，f（x）＜0；当x＞0时，f（x）＞0.

（2）若x=0是f（x）的极大值点，求a.

分析：本题两问都可以用常规解法解答.对于第（1）问，

求导，利用函数单调性证明即可；对于第（2）问，

分a≥0和a<0进行讨论，构造函数h（x）=f（x）2+x+ax2，讨论h（x）的性质即可得到a的范围.其中第（2）问还可以利用极值的第三充分条件和泰勒展开求解.

（Ⅱ）（2021年乙卷第10题）

设a≠0，若x=a为函数f（x）=a（x－a）2（x－b）的极大值点，则（）.

A.a<b

B.a>b

C.ab<a2

D.ab>a2

6 试题价值

新课程标准中对导数在函数中的应用提出的要求是：“借助函数图象，了解函数在某点取得极值的必要条件和充分条件.”本题深入贯彻了课标要求，考查了极值点的充分条件，此部分的内容新教材涉及不多，且解答此类问题需要部分高等数学知识，这也提醒了教师在之后的教学中需要渗透部分必要的高等数学思想，利用这些思想可以帮助我们解出题目中要求的参数范围，进而再用高中数学的基本方法证明此范围的充要性，这也对今后学生的数学抽象和逻辑推理核心素养提出了更高的要求.