2023年数学新高考Ⅰ卷第12题的探究

高考是学生人生中的第一次大考，关乎着人生的走向，所以高考试题的变化牵动着亿万学生及家长的心.2023年数学新高考Ⅰ卷的第12题对正方体、球、棱锥、圆柱进行了综合考查.其中D选项难度较大，而且在网上给出的答案中，对D选项的说明是：圆柱高度可以忽略不计.这种解释在以往的解答中没有遇到过，它给课堂教学提出了新的问题.其实利用图形软件和高中数学知识，还是可以通过计算解决问题的.

1 试题呈现

（2023年数学新高考Ⅰ卷·第12题）（多选题）下列物体中，能够被整体放入棱长为1（单位：m）的正方体容器（容器壁厚度忽略不计）内的有（ ）.

A.直径为0.99 m的球体

B.所有棱长均为1.4 m的四面体

C.底面直径为0.01 m，高为1.8 m的圆柱体

D.底面直径为1.2 m，高为0.01 m的圆柱体

2 试题解析

对于A选项的考查非常简单，由于球的直径小于

正方体的棱长，故球体可以放入正方体容器内，如图1所示.

对于选项B，可以理解为从棱长为1 m的正

方体中，截出的最大正四面体（如图2）的棱长为2m，大于1.4 m，故可以放进正方体容器内.

在C选项中，圆柱的高度为1.8 m，而棱长为

1 m的正方体的体对角线的长度为3 m，由于1.8大于

3，故选项C不正确.

对D选项的判断是本题的难点.首先，我们要解决的问题是，直径为1.2 m的圆是否可以放进正方体内;其次，再解决圆柱的高度问题.在正方体的所有截面中，面积最大的是哪个？其实这个问题在2018年的高考中已经出现过了.

（2018全国Ⅰ卷·理科数学第12题）已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得的截面面积的最大值为（ ）.

A.334

B.233

C.324

D.32

分析：如图3，当截面过正方体中心，且与体对角线垂直的时候，截面面积最大，此时截面与正方体各个棱的交点M，L，K，J，I，N为所在边的中点，多边形MLKJIN为正六边形（如图4），边长为22，其面积可以利用六个边长为22的正三角形来计算，结果为334，故选择A选项.

由于圆柱的高为0.01 m，比较小，可以忽略不计，因此只要考虑直径为1.2 m的圆是否可以放入正方体内即可，也就是正六边形MLKJIN的内切圆（如图5）直径是否大于1.2 m.

易得内切圆圆心O到边IJ的距离为64.

同理，圆心O到边ML的距离也为64，则正六边形内切圆的直径为62.

因为62=1.5>1.2=1.44，所以

直径为1.2 m的圆可以放入正六边形MLKJIN中.由于圆柱的高度忽略不计，因此可得，圆柱可以放入正方体内.

圆柱的高度忽略不计这种情况在平时没有遇到过，学生很难想到，即使在看到答案后，也不是完全接受这种作答方法.那么，是否能够计算出正方体内部可以放入底面直径为1.2 m的圆柱的最大高度呢？

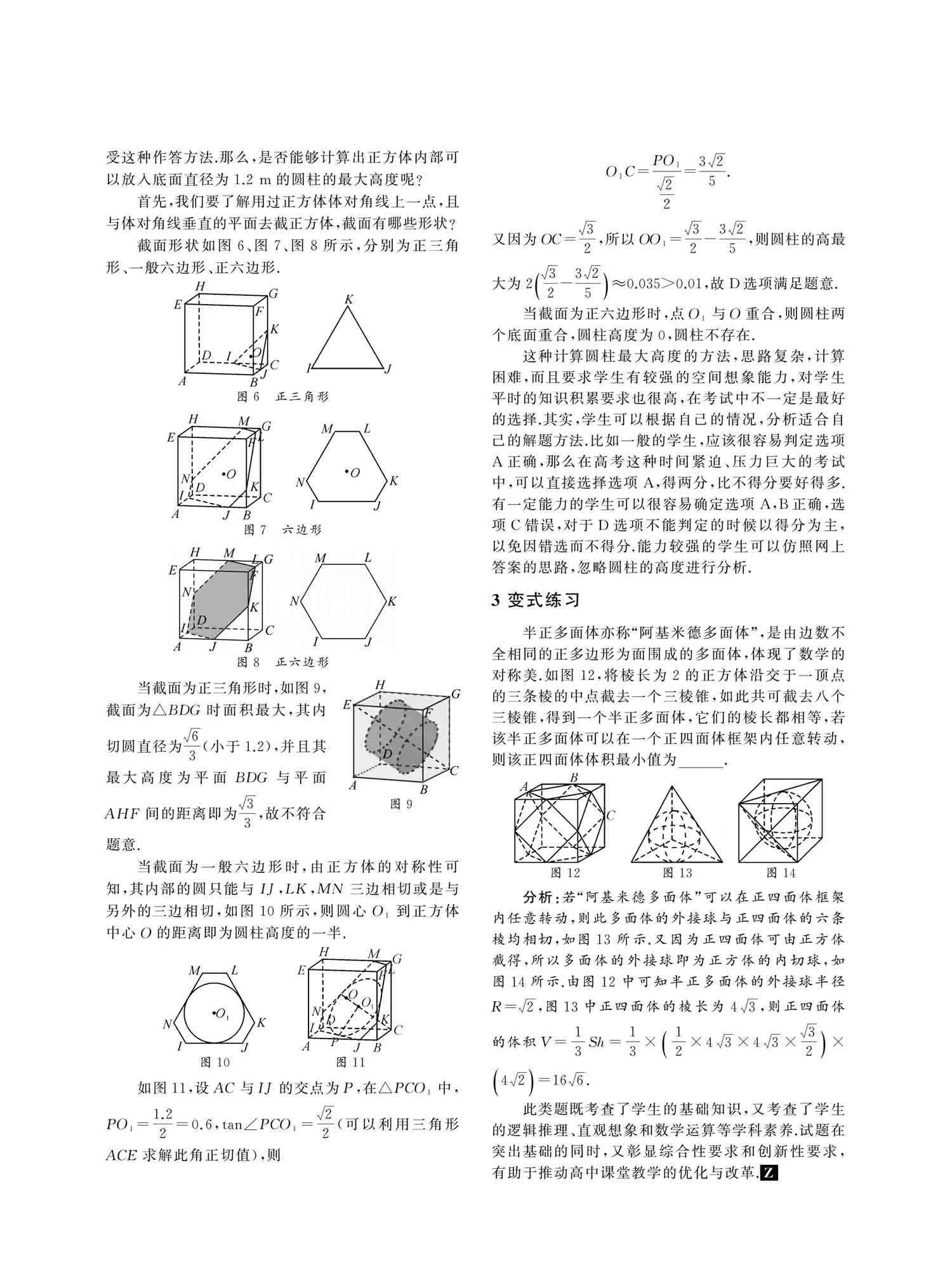
首先，我们要了解用过正方体体对角线上一点，且与体对角线垂直的平面去截正方体，截面有哪些形状？

截面形状如图6、图7、图8所示，分别为正三角形、一般六边形、正六边形.

当截面为正三角形时，如图9，截面为△BDG时面积最大，其内切圆直径为63（小于1.2），并且其最大高度为平面BDG与平面AHF间的距离即为33，故不符合题意.

当截面为一般六边形时，由正方体的对称性可知，其内部的圆只能与IJ，LK，MN三边相切或是与另外的三边相切，如图10所示，则圆心O1到正方体中心O的距离即为圆柱高度的一半.

如图11，设AC与IJ的交点为P，在△PCO1中，PO1=1.22=0.6，tan∠PCO1=22（可以利用三角形ACE求解此角正切值），则

O1C=PO122=325.

又因为OC=32，

所以OO1=32-325，则圆柱的高最大为232-325≈0.035>0.01，故D选项满足题意.

当截面为正六边形时，点O1与O重合，则圆柱两个底面重合，圆柱高度为0，圆柱不存在.

这种计算圆柱最大高度的方法，思路复杂，计算困难，而且要求学生有较强的空间想象能力，对学生平时的知识积累要求也很高，在考试中不一定是最好的选择.其实，学生可以根据自己的情况，分析适合自己的解题方法.比如一般的学生，应该很容易判定选项A正确，那么在高考这种时间紧迫、压力巨大的考试中，可以直接选择选项A，得两分，比不得分要好得多.有一定能力的学生可以很容易确定选项A，B正确，选项C错误，对于D选项不能判定的时候以得分为主，以免因错选而不得分.能力较强的学生可以仿照网上答案的思路，忽略圆柱的高度进行分析.

3 变式练习

半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形为面围成的多面体，体现了数学的对称美．如图12，将棱长为2的正方体沿交于一顶点的三条棱的中点截去一个三棱锥，如此共可截去八个三棱锥，得到一个半正多面体，它们的棱长都相等，若该半正多面体可以在一个正四面体框架内任意转动，则该正四面体体积最小值为______.

分析：若“阿基米德多面体”可以在正四面体框架内任意转动，则此多面体的外接球与正四面体的六条棱均相切，如图13所示.又因为正四面体可由正方体截得，所以多面体的外接球即为正方体的内切球，如图14所示.由图12中可知半正多面体的外接球半径R=2，图13中正四面体的棱长为43，则正四面体的体积V=13Sh=13×12×43×43×32×42=166.

此类题既考查了学生的基础知识，又考查了学生的逻辑推理、直观想象和数学运算等学科素养.试题在突出基础的同时，又彰显综合性要求和创新性要求，有助于推动高中课堂教学的优化与改革.