指向核心素养的高中数学作业分层指标体系研究

摘要：本文旨在优化数学分层作业设计研究中作业分层依据，注重学生核心素养的发展.采用德尔菲法确定作业分层指标体系为数学核心素养、问题情境、知识含量、推理能力、运算水平、阅读量等6大因素，并确定18项二级指标.利用层次分析法获得各级指标的权重，构建作业分层指标体系，为高中数学教师进行分层作业设计提供作业分层的参考依据.

关键词：数学核心素养；作业分层；综合难度系数

《普通高中数学课程标准（2017年版2020年修订）》明确指出，数学核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用的过程中逐步形成和发展的［1］.培养学生数学核心素养是高中数学教学的基本要求，要深入到教学的各个环节.武丽莎等［2］教授表明，数学核心素养生成的本源是数学知识，本旨是问题解决，本质是数学思维.课堂教学是数学知识生成的主要环节，作业是数学问题解决和数学思维发展的主要环节.因此，如何将数学核心素养融入作业设计是一个重要的研究问题.而分层作业设计基于因材施教原则，从学生实际情况出发，促进学生的个性化发展.到目前为止，有许多学者对数学分层作业设计进行研究和实践，但研究中的重点作业分层还有待优化.基于此，本文探究在指向核心素养的高中数学分层作业设计中如何进行作业分层.

1 作业分层指标选取

指向核心素养的高中数学分层作业设计中作业分层需要综合考虑数学核心素养和影响数学作业难度的因素.喻平［3］教授根据布卢姆模型、PISA模型和SOLO模型，将数学核心素养分成知识理解、知识迁移和知识创新三种水平.所以，本文中将数学核心素养作为作业分层的其中一个一级指标，并将知识理解、知识迁移和知识创新作为其二级指标.

关于影响作业难度的因素，鲍建生［4］教授根据Nahara的总体难度概念提出了综合难度系数模型，认为影响数学题难度的主要因素有探究、背景、运算、推理和知识含量；卢建川、武小鹏、薛欢等提出影响数学试题难度的还有数学认知、是否含参、思维方向、条件含量和阅读量等因素.由文献分析可知，背景、知识含量、推理、运算和阅读量等是影响数学作业难度的主要因素.

背景实际上是数学核心素养中的情境，主要是指现实情境、数学情境、科学情境［1］.因此，本文中将问题情境纳入作业分层的一级指标，并将数学情境、现实情境和科学情境作为其二级指标.

对于知识含量，在核心素养的研究中，喻平［5］提出学习的结果是形成个体知识，个体知识是学科关键能力生成的基础.不同的知识对应不同的数学核心素养，在一个知识的学习中无法发展六种数学核心素养，而知识的综合应用体现着核心素养的综合发展.本文中将知识含量纳入作业分层的一级指标，并将单个知识、两个知识和多个知识作为其二级指标.

周雪兵［6］提出逻辑推理是得到数学结论、构建数学体系的重要方式，是人们在数学活动中进行交流的基本思维品质.史宁中教授将“数学的思维”归结为逻辑推理和数学运算.逻辑推理是从一些前提或事实出发，依据一定规则得到或验证命题的思维过程［7］.逻辑推理形成了数学的严谨性这一基本特征.本文中将推理能力纳入作业分层的一级指标，并将简单推理和复杂推理作为其二级指标.

作业难度因素中的运算，史宁中表明数学运算属于逻辑推理，但数学运算非常重要，因此将其作为核心素养的一个要素提出.本文中将运算水平纳入作业分层的一级指标，并将简单数值运算、复杂数值运算、简单符号运算和复杂符号运算作为其二级指标.

阅读量强调学生阅读能力，由于数学符号语言的抽象性特点，学生在数学阅读中需要进行思维转换，从而使客观知识转化为个人知识.王旭勤［8］提出阅读能力能够提高学生自主学习和探究能力，逐步发展学生数学核心素养.本文中将阅读量纳入作业分层的一级指标，并将阅读量的少量、中等和大量作为其二级指标.

2 作业分层指标确定

根据上述分析，初步设定指向核心素养的高中数学作业分层一级指标为数学核心素养、问题情境、知识含量、推理能力、运算水平和阅读量6项，以及相应的18项二级指标.

本文中采用德尔菲法，选取高校相关研究领域专家7名，资深高中数学教师8名，总共15名，展开问卷调查.根据问卷数据，计算每一项指标的均值、标准差和变异系数，根据专家提出的修改意见，对指标进行进一步检验和修改，最后确定作业分层指标体系，具体如表1所示.

3 作业分层指标权重

指标体系中各项指标的权重，反映其在指标体系中的地位、作用和重要程度.在上述确定的作业分层指标体系的基础上，借助层次分析法获取作业分层指标体系中各项指标的权重.具体步骤如下：

（1）建立指向核心素养的高中数学作业分层指标体系递阶层次结构模型，设定目标层为指向核心素养的高中数学作业分层，准则层为6项一级指标，方案层为18项二级指标.

（2）采用9点法，设置指标评分标度，专家根据指标重要程度标度值对指标进行打分，取15位专家评分均值作为指标评分值，构建两两比较判断矩阵.

（3）将判断矩阵进行层次归一化，计算各判断矩阵的权重向量.

①判断矩阵每一列归一化：bij=aij∑ni=1aij，其中aij表示判断矩阵的第i行，第j列的值；

②归一化后的矩阵按行求和：Vi=∑nj=1bij，其中bij表示判断矩阵第i行，第j列归一化后所得值；

③求和后的矩阵归一化，得到权重向量：Wi=Vi∑ni=1Vi，其中Vi表示归一化的矩阵第i行求和后的值，Wi表示权重向量第i行的值.

（4）计算出各指标权重向量值后，对归一化的矩阵进行一致性检验.

①计算矩阵特征根λmax，λmax=∑ni=1（AW）inWi，其中n是指标数，A是判断矩阵，W是权重向量，（AW）i是向量AW第i个元素.

②计算随机一致性比值CR，CI=λmax－nn－1，CR=CIRI，n是指标数，λmax是矩阵特征根.根据随机一致性比例系数取值参考表，对所有一级指标和二级指标矩阵进行检验，若得到构建的指标权重矩阵CR<0.1，则说明具有一致性，指标权重可用.

最后得到作业分层指标体系中各一级指标和二级指标的权重值，具体如表2所示.

对于给定的一道作业题，利用本表即可查得该题的难度系数，具体计算公式如下：本题的难度系数等于各一级指标对应本题某个二级指标的组合权重之和.

4 案例分析

根据上述确定的作业分层指标体系表2及计算公式，教师或教研组对数学课后作业进行分题型分层设计，根据学生实际情况，设定层次综合难度.下面以2019人教A版高中数学教材必修一第4章“函数模型的应用”的习题中指数函数模型的应用题为例，具体说明指标体系的使用方法.

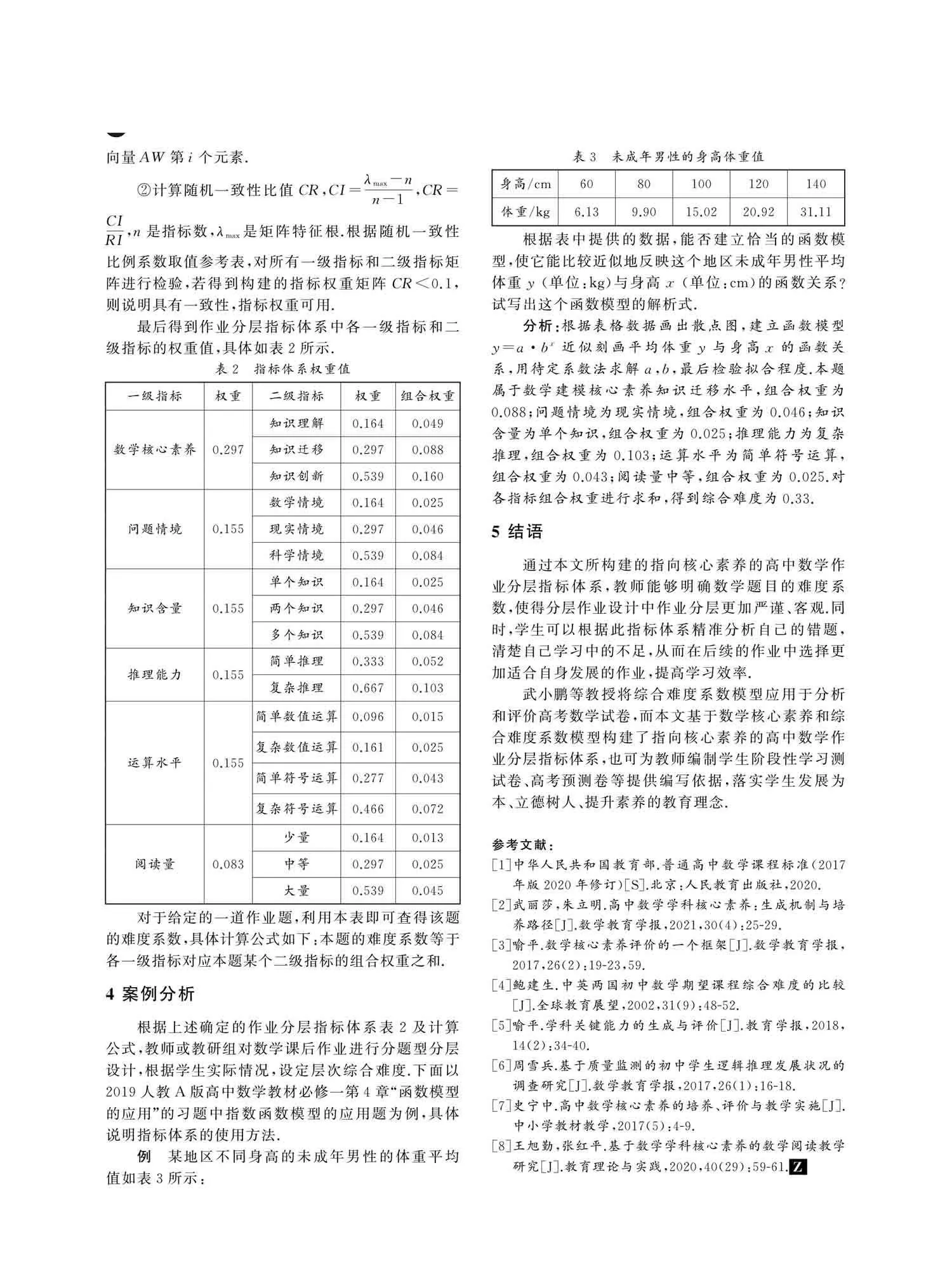
例 某地区不同身高的未成年男性的体重平均值如表3所示：

根据表中提供的数据，能否建立恰当的函数模型，使它能比较近似地反映这个地区未成年男性平均体重y （单位：kg）与身高x （单位：cm）的函数关系？试写出这个函数模型的解析式.

分析：根据表格数据画出散点图，建立函数模型y=a·bx近似刻画平均体重y与身高x的函数关系，用待定系数法求解a，b，最后检验拟合程度.本题属于数学建模核心素养知识迁移水平，组合权重为0.088；问题情境为现实情境，组合权重为0.046；知识含量为单个知识，组合权重为0.025；推理能力为复杂推理，组合权重为0.103；运算水平为简单符号运算，组合权重为0.043；阅读量中等，组合权重为0.025.对各指标组合权重进行求和，得到综合难度为0.33.

5 结语

通过本文所构建的指向核心素养的高中数学作业分层指标体系，教师能够明确数学题目的难度系数，使得分层作业设计中作业分层更加严谨、客观.同时，学生可以根据此指标体系精准分析自己的错题，清楚自己学习中的不足，从而在后续的作业中选择更加适合自身发展的作业，提高学习效率.

武小鹏等教授将综合难度系数模型应用于分析和评价高考数学试卷，而本文基于数学核心素养和综合难度系数模型构建了指向核心素养的高中数学作业分层指标体系，也可为教师编制学生阶段性学习测试卷、高考预测卷等提供编写依据，落实学生发展为本、立德树人、提升素养的教育理念.

参考文献：

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［S］.北京：人民教育出版社，2020.

［2］武丽莎，朱立明.高中数学学科核心素养：生成机制与培养路径［J］.数学教育学报，2021，30（4）：25-29.

［3］喻平.数学核心素养评价的一个框架［J］.数学教育学报，2017，26（2）：19-23，59.

［4］鲍建生.中英两国初中数学期望课程综合难度的比较［J］.全球教育展望，2002，31（9）：48-52.

［5］喻平.学科关键能力的生成与评价［J］.教育学报，2018，14（2）：34-40.

［6］周雪兵.基于质量监测的初中学生逻辑推理发展状况的调查研究［J］.数学教育学报，2017，26（1）：16-18.

［7］史宁中.高中数学核心素养的培养、评价与教学实施［J］.中小学教材教学，2017（5）：4-9.

［8］王旭勤，张红平.基于数学学科核心素养的数学阅读教学研究［J］.教育理论与实践，2020，40（29）：59-61.