统计图表创新题中的数据分析素养

图表信息题是涉及题设条件或结论中包含有图表及其对应信息的试题.用图表形式提供信息，与以往通过单一文字叙述等方式提供信息相比较，往往有更加直观、信息量大、数量之间关系明确等优点，成为近年高考数学命题的热点之一.此类问题一般以真实的生活实例为情境命题，如国家统计局公布的一些统计数据等，对考生读图、识图及数据处理的能力提出了较高的要求.高中数学除了最常见的频率分布直方图和茎叶图外，常见的统计图表还有扇形图（饼图）、柱（条）形图、折线图、雷达图等.

1 扇形图（饼图）

扇形图（或饼图），又称扇形统计图，其是借助整个圆及其内部区域表示总数，而利用圆内各个不同扇形的大小区域来表示各小部分数量占总数的百分数或比例关系.通过扇形统计图，可以很清楚地表示出各部分数量同总数之间的关系.

例1 〔2023年湖北省武汉市高考数学调研试卷（4月份）〕（多选题）某市2022年经过招商引资后，经济收入较前一年增加了一倍，实现翻番，为更好地了解该市的经济收入的变化情况，统计了该市招商引资前后的年经济收入构成比例，得到如下扇形图（图1）：

则下列结论中正确的是（ ）.

A.招商引资后，工资性收入较前一年增加

B.招商引资后，转移净收入是前一年的1.25倍

C.招商引资后，转移净收入与财产净收入的总和超过了该年经济收入的25

D.招商引资后，经营净收入较前一年增加了一倍

解析：设招商引资前经济收入为a，则招商引资后经济收入为2a.

对于选项A，招商引资前工资性收入为0.6a，招商引资后工资性收入为0.37×2a=0.74a，因为0.74a>0.6a，所以招商引资后工资性收入较前一年增加了，故选项A正确；

对于选项B，招商引资前转移净收入为0.04a，招商引资后转移净收入为0.05×2a=0.1a，因为0.1a0.04a=2.5，所以招商引资后，转移净收入是前一年的2.5倍，故选项B错误；

对于选项C，招商引资后，转移净收入与财产净收入的总和占33%<40%，所以招商引资后，转移净收入与财产净收入的总和不超过该年经济收入的25，故选项C错误；

对于选项D，招商引资前经营净收入为0.3a，招商引资后经营净收入为0.3×2a=0.6a，所以招商引资后，经营净收入较前一年增加了一倍，故选项D正确.

故选择答案：AD.

点评：抓住扇形图（饼图）这一统计图表的图形特征，明确扇形当中各个对应数据所对应的实际含义以及占总体圆形的百分比等相关数据信息，有时还根据需要将数据信息通过表格列出，进而再合理进行数据分析、数学运算、判断应用等.

2 柱（条）形图

柱（条）形图是指用宽度相同的柱（条）形的高度或长短来表示数据信息的一种图形，可以横置或纵置（此时叫做柱形图）.柱（条）形图可以借助高度或长短来分析数据信息与变化规律等.

例2 〔2023年四川省遂宁市射洪中学高三（下）第一次月考数学试卷〕“90后”指1990年及以后出生，“80后”指1980—1989年之间出生，“80前”指1979年及以前出生.某调查机构对全国互联网行业进行调查统计，得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图（图2），则下列结论中不一定正确的是（ ）.

A.互联网行业从业人员中90后占一半以上

B.互联网行业中从事技术岗位的人数超过总人数的20%

C.互联网行业中从事运营岗位的人数90后比80前多

D.互联网行业中从事技术岗位的人数90后比80后多

解析：对于选项A，由饼状图中可知90后的占比为56%，故选项A正确；

对于选项B，由条形图知90后从事技求岗位的占比为39.6%，结合选项A中信息，有56%×39.6%=22.176%，超过总人数的20%，故选项B正确；

对于选项C，由条形图知90后从事运营岗位的占比为17%，结合选项A中信息，有56%×17%=9.52%，而由饼状图知80前的占比3%，故选项C正确.

综上分析，故选择答案：D.

3 折线图

折线图是将排列在工作表的行或列中的数据可以绘制到相应的坐标系中，各点之间通过折线加以连接而形成.折线图可以显示随着时间（根据常用比例设置）而变化的连续数据，合理显示上升或下降趋势以及图形的波动性情况等，同时注意横轴与纵轴数据的实际含义以及对应的数值等信息.

例3 （2023年浙江省宁波市高考数学二模试卷）（多选题）根据某地3月5日到3月15日的每天最高气温与最低气温数据（单位：℃）绘制如下折线图（图3），那么下列叙述正确的是（ ）.

A.5日到11日的最低气温与日期之间呈线性相关关系且为正相关

B.9日的最高气温与最低气温的差值最大

C.最高气温的众数为27℃

D.5日到15日的最低气温的极差比最高气温的极差大

解析：由5日到11日的最低气温的散点分布是从左下到右上可知，最低气温与日期之间呈线性相关关系且为正相关，故选项A正确；

由图可知，6日的最高气温与最低气温的差值最大，故选项B错误；

最高气温27℃出现了两次，其他数据都只出现了1次，所以27℃是最高气温的众数，故选项C正确；

5日到15日的最低气温的极差小于15－3=12，而5日到15日的最高气温的极差约等于27－15=12，故选项D错误.

故选择答案：AC.

4 雷达图

雷达图是以从同一点开始的轴上表示的三个或更多个定量变量的二维图表的形式显示多变量数据的图形方法.轴的相对位置和角度通常是无信息的，它相当于平行坐标图，轴径向排列.

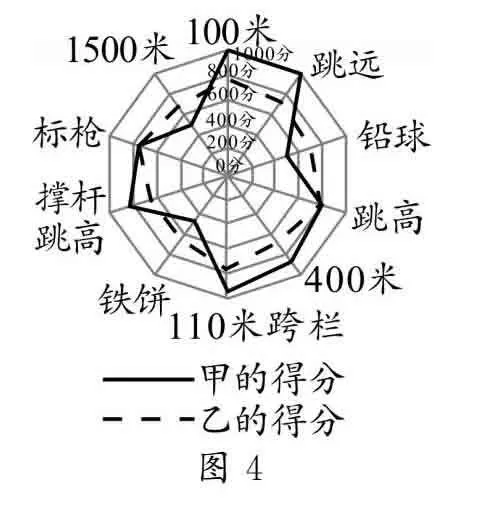
例4 （2023年河南省创新发展联盟高考数学二模试卷）作为田径运动中全能项目的一种——十项全能是由跑、跳、投等10个基本田径项目组成的一个综合性男子比赛项目，比赛成绩是按照国际田径联合会制定的专门田径运动会全能评分表将各个单项成绩所得的评分加起来计算的，总分多者为优胜者.如图4，这是某次十项全能比赛中甲、乙两名运动员的各个单项得分的雷达图，则下列说法正确的是（ ）.

A.在400米跑项目中，甲的得分比乙的得分低

B.甲的各项得分比乙的各项得分更均衡

C.在跳高和铁饼项目中，甲、乙水平相当

D.甲的各项得分的极差比乙的各项得分的极差大

解析：由雷达图可知，400米跑项目中，甲的得分比乙的得分高，选项A错误；

甲各项得分的波动较大，乙的各项得分均在（600，800］内，波动较小，选项B错误；

在铁饼项目中，乙比甲水平高，选项C错误；

甲的各项得分的极差约为1 000－470=530，乙的各项得分的极差小于200，选项D正确.

故选：D.

解答统计图表创新试题，需仔细观察图表，挖掘图表所含的数据信息，对所得到数据信息进行分类、合成、提取、加工等处理，结合统计相关知识加以合理逻辑推理或数学运算等，最终求得问题的答案，很好地考查考生数学基础知识与数学基本能力，培养数据分析素养以及创新意识与应用能力等.