基于“生本”理念的“一题一课”教学实践探究

摘要：三角函数是高考中每年必考的内容，其中的“给值求值”问题更是屡见不鲜.本文中以“三角函数中给值求值问题”为例，通过“一题一课”的课堂教学模式，充分提取教材中的典型例题、课后习题等素材进行“再加工、再整合”，开展探究活动，落实生本理念，从而提高学生的数学理解能力，助推学生的思维水平走向高阶.

关键词：给值求值；生本理念；一题一课；教学实践

“生本教育”是郭思乐教授创立的一种教育思想和教育方式.生本教育是以“一切为了学生，高度尊重学生，全面依靠学生”为宗旨的教育，它既是一种方式，更是一种理念.

所谓“一题一课”［1］，就是指教师通过对一道题或某一素材的深入研究，挖掘其中蕴含的数学本质与内涵，科学、合理、有序地组织学生进行相关的数学探究活动，促进学生对知识之间的关联性理解，实现“学一题，透一点，通一类”的教学目标.

1 挖掘探究材料

1.1 课时内容分析

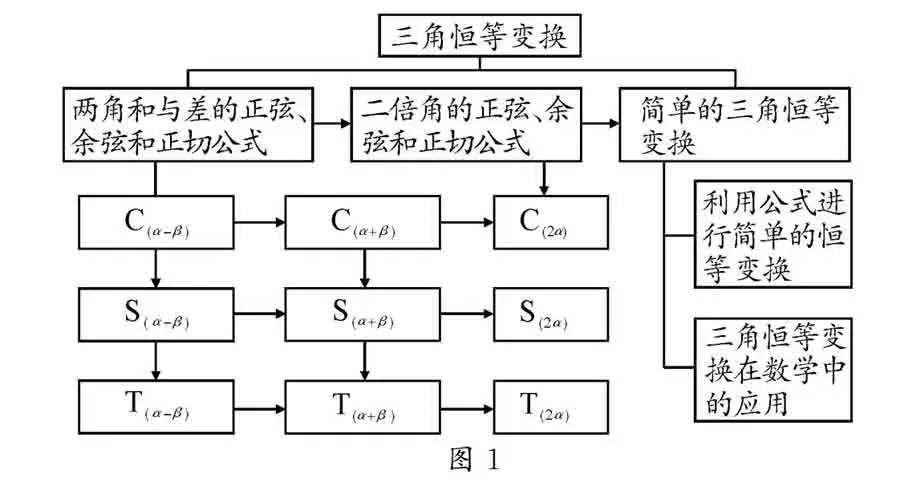
“三角恒等变换”的知识结构［2］如图1.

通过本节内容的学习，学生能够掌握解决简单三角恒等变换的方法，同时在三角函数的简单恒等变换的运算中可以有效训练逻辑推理能力和数学运算能力.

1.2 教学内容分析

本节课内容来自人教A版必修第一册第五章第五节“三角恒等变换”，变换是数学的重要工具，也是数学学习的主要对象之一.代数变换是学生所熟悉的，与代数变换一样，三角变换也是只变其形而不变其质.本节课，学生将运用两角和与差的正弦、余弦公式，进行简单的三角变换，利用凑角的方法解决给值求值问题.通过本节课的学习，学生的逻辑推理能力和运算能力将得到进一步提高.

1.3 学生情况分析

学生较好地掌握了两角和与差的正弦、余弦、正切公式及其公式的简单应用，这为认识三角变换提供了基础；但对公式还不熟悉，其理解还停留在公式的表象认知，需要教师的分析、引导.

1.4 例题与练习分析

由表1可见，教材对给值求值的要求是很高的，需要学生掌握其运算规律及解决方法，本节课的重点是使学生学会用凑角的方法，用已知角表示出未知角从而求出所求角的三角函数值.

1.5 确定教学目标

为了让学生深度理解给值求值问题的解决方法，特确定本节课的教学目标为：

（1）理解三角恒等变换的根本思想，通过观察角之间的关系，利用凑角化未知角为已知角，培养整体代换和换元思想，理解化归思想；

（2）能独立分析和解决一些三角恒等变换“给值求值”问题；

（3）能够灵活运用公式，提高逻辑推理和数学运算能力.

1.6 评价任务

（1）入门测要求学生自主完成，并通过入门测涉及到的两角和与差的正弦、余弦、正切公式进行复习回顾；

（2）通过变式训练的分析讲解，挖掘三角函数中给值求值问题所涉及到的整体思想，同时提炼解题方法——“凑角”.

2 设计探究过程

2.1 课前自测

入门测：若sin α=13，α∈π2，π，求sinα+π4的值.

此题需学生课前完成，其完成情况如下：

学生1：利用三角恒等式及已知条件sin α=13，可以求出cos α的值，进而运用两角和的正弦公式求值即可.

教师：思路没有问题，但是否严谨，其他同学有补充吗？

学生2：利用三角恒等式求cos α的值时，要注意角所在象限.

教师：非常好，我们在运用三角恒等式求解的时候要注意角所在象限，从而决定取值的正负.

师生活动：教师运用希沃软件拍照展示学生的解答过程，规范解题步骤.

说明：通过两角和的正弦公式的简单应用，提醒学生在利用三角恒等式求解时要注意角所在象限，避免出现错解.

2.2 探究解题方法

为了实现“学一题，透一点，通一类”的教学目标，运用“一题一课”的教学模式，特设置如下变式问题串供学生探究.

变式1 若sinα+π4=13，α∈π2，π，求sin α的值.

教学预设：本题有部分学生会利用两角和的正弦公式将sinα+π4=13，展开，并结合三角恒等式联立方程组求解；另有部分学生会发现α=α+π4－π4，然后利用两角差的正弦公式求解.两种不同的解法其运算过程的繁杂程度明显不同，第一种方法思路简单但运算量较大，第二种方法技巧性较强但计算量明显减小.在此进行铺垫说明：将复杂的问题简单化就是数学中常说的化归思想;我们把用已知角表示出未知角的方法叫做“凑角”.

说明：通过两种不同解题思路的对比，学生能够体会到“凑角”方法的优势.由此为深层次讲解“凑角”方法做好铺垫.

变式2 若sin（α+β）=13，cos β=45，α∈π2，π，β∈0，π2，求sin α与sin（α+2β）的值.

教学预设：变式1讲评结束，教师引导学生观察变式2中已知角与未知角的关系，通过小组交流可以发现α=（α+β）－β，α+2β=（α+β）+β，此时学生可以轻松利用两角和与差的正弦公式解题.在解题过程中要提示学生注意角所在象限，从而决定取值的正负.

说明：通过变式1与变式2的类比，学生能够进一步感知利用整体思想进行凑角的便利，同时感受由特殊到一般的方法，进而提升归纳推理能力.

变式3 已知sinα+π4=13，sin（α+β）=－45，α∈π2，π，β∈0，π2，求sinβ－π4的值.

说明：通过增加已知角的难度，学生可以学会“举一反三”，体会数学化归思想.

2.3 总结提升

出门测：

（1）已知cos α=45，α∈3π2，2π，求cosα－π3的值.

（2）若α，β均为锐角，且sin α=13，cos（α+β）=－35，求sin β的值.

（3）若sin 2α=55，sin（β－α）=1010，α∈π4，π，β∈π，3π2，求cos（α+β）的值.

说明：设置出门测是为了让学有余力的学生在学习新知识的基础上做进一步探究学习，进而培养他们的应用意识，提高他们的数学思维能力.

课时小结：通过这节课的学习，你有什么收获？

说明：教师引导学生总结归纳本节课的收获，可以有效地帮助学生构建知识框架，对所学的新知识快速做到融会贯通，灵活应用.

3 反思实践过程

“一题一课”课堂教学模式旨在聚焦“一题”，延伸“一课”，充分挖掘典型例题背后蕴含的价值，利用变式练习实现知识的内化，使学生的认知从特殊走向一般，化未知为已知.

本节课是笔者在集团校的一节送教展示课，反响还不错.纵观本节课，利用具有知识生成逻辑的“变式练习”来授课，在具体的数学探究变式中让学生体验、内化数学知识，逐步学会将复杂问题简单化的化归思想.笔者认为本节课的成功得益于以下几个方面.

（1）以生为本

学生是学习的主人，本节课以学生已经认识并熟知的两角和与差公式的简单变形应用的入门测小练习引入，使得学生对将要学习的新知识没有畏惧感，有利于课堂教学的顺利开展.

（2）以课本为纲

课本是学生学做人做事的基本载体，脱离课本的教学不是好的数学教学.教师最基本且重要的职责是教好课本，而本节课恰恰是立足于教材的典型例题和课后习题，并进行深入探究而开展的教学活动.

（3）以课堂为基

课堂是教学工作的主阵地，是学生获取知识与能力的主要途径，本节课以“一题一课”的课堂教学模式来开展，使教学活动自然流畅，教学目标基本达成.

参考文献：

［1］王先义.基于“生本”理念的“一题一课”微专题复习课探究以——“含参函数零点问题”为例［J］.中学数学月刊，2023（1）：21-26.

［2］石雨卓.小专题，大功能——“探究函数y=ax+bx的图像与性质”教学实践与反思［J］.中学数学教学参考，2023（1）：35-37.