基于RMI原则的函数图象变化教学

摘要：RMI原则（关系映射反演原则）所强调的转换思想是数学中的一种重要思维.对于高中数学学习中的重难点函数y=Asin（ωx+φ），使用RMI原则，在动态几何软件的支持下，对函数y=Asin（ωx+φ）进行多重表征，帮助学生理解参数A，φ，ω的含义，并利用RMI原则解决学习过程中容易产生的认知冲突，帮助学生提升关于函数y=Asin（ωx+φ）的学习表现.

关键词：RMI原则；函数y=Asin（ωx+φ）；动态几何软件

1 问题提出

《普通高中数学课程标准（2017年版2020年修订）》中提到，利用单位圆帮助学生理解三角函数的定义.与具体实例相结合，了解函数y=Asin（ωx+φ）的实际意义;能利用函数的图象理解参数A，ω，φ的含义，了解A，ω，φ的变化对三角函数图象的影响［1］.

在数学史上，三角函数也叫做“圆函数”，因为研究圆周运动的需要产生了任意角的三角函数.因此任意角的三角函数是一个周期函数，章建跃［2］老师称其是研究现实世界中周期变化现象的“最有表现力的函数”.故利用单位圆来表示任意角三角函数就能清晰明了地表达出三角函数的周期性.由上所述，既然单位圆能够清晰明了表达任意角三角函数的周期性，那么将单位圆和三角函数图象相结合，能否简洁明了地表示出参数A，ω，φ对三角函数图象变换的影响？笔者试图解决以下问题：基于RMI原则，在动态几何软件支持下的函数y=Asin（ωx+φ）教学中，通过对三角函数图象的多重表征，以及认知冲突的解决能否提升学生的学习表现？

2 RMI原则与三角函数多重表征

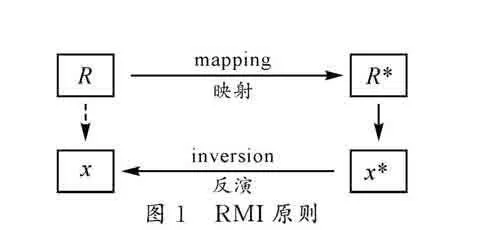
RMI原则即关系映射反演原则.如图1，在数学中，会存在给定一个关系结构系统R，其含有一个原像x.为了求解原像x，需要找到一个可逆映射，该映射可将R变为R*，此时能从R*中寻找出映像x*.最后通过对映像x*反演得到原像x，从而解决问题［3］.

RMI原则强调的是一种化归

思想，即把一种复杂的数学问题映射为一

个新的容易解决的数学问题.故在数学教学过程中，将由于数学的抽象性所导致的学生学习遇到的一些抽象的、远离学生生活的数学概念通过转换，化为直观的、可视的图象进行理解.

在数学概念学习过程中常用

多重表征来表示一个概念，从而促进学生

对概念的理解、记忆和应用.如函数，可

以通过列表法、图象法和解析式法来表

示．通过对函数y=Asin（ωx+φ）进行图象表征和代数表征，提升学生数形结合能力，在数和形的转换过程中加深对参数A，ω，φ的理解，并将其应用在数学问题的解决中.

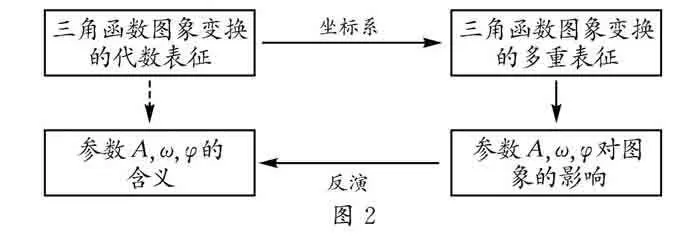
如图２

，在动态几何软件条件下，利用RMI原则将函

数y＝Asin（ωx＋φ）中参数A ，φ，ω的代数表征映射为图象表征，通过图象表征理解参数A ，ω，φ的含义，从而了解A，ω，φ的变化对三

角函数图象的影响．

师生活动：教师帮助学生认识点的平移和函数平移的关系.如图7，根据RMI原则，

引导学生将函数y＝

sin ωx 和函数y＝sin（ωx＋φ

）建立映射关系．函数y ＝sin（ωx＋φ），当t＝－φ

ω时得到点

-φω，0，对其进行反演得到函数y=sin ωx的点（0，0）.

4 结论

根据RMI原则，将动态几何软件与三角函数图象变化相结合进行课堂教学，让学生对参数A，ω，φ蕴含的平移、伸缩变化规律有了直观形象的理解.

这样的教学创造了一

个动态、直观的学习情境，建立多

重表征形式加深学生的理解，提

升学生学习表现

.但提升学习效果的不仅仅是RMI原则和动态几何软件本身，还有能够与其充分结合的教学方法和内容，即要根据具体的内容选择能有效改善学生学习情景的技术手段.

RMI原则本质是一种方法论原则，教师利用RMI原则以高观点的视角进行教学，解决学生遇到的认知冲突并将映射反演的思维方式渗透给学生，能够帮助学生理解知识，提升分析问题和解决问题的能力，厘清思维过程，培养发散性思维.

参考文献：

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［S］.北京：人民教育出版社，2020.

［2］章建跃.为什么用单位圆上点的坐标定义任意角的三角函数［J］.数学通报，2007（1）：15-18.

［3］江春莲，胡玲.基于APOS理论和RMI原则的二次函数图象平移教学实验研究［J］.数学教育学报，2020，29（6）：32-39.