线上线下深度融合的高三数学复习课探究

摘要：“O2O”教学模式可以拓展教学的时间和空间，丰富教学资源，推进个性化教学的发展.

针对线上线下深度融合的高三复习课探究，

教师结合艺术生的学习现状，根据“O2O”教学模式的基础理论，将该模式融入高三一轮复习中，探索适合学生的线上线下深度融合教学路径.

关键词：线上线下；深度融合；“O2O”教学模式；高三

1 “O2O”教学模式概述

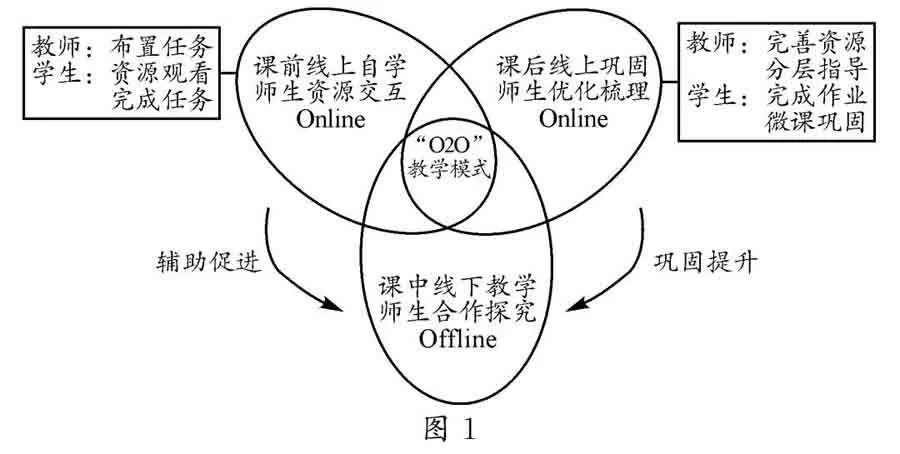
《普通高中数学课程标准（2017年版2020年修订）》（以下简称《标准》）指出：注重信息技术与数学课程深度融合，优化课堂教学，提高教学实效性，引导学生自主获取资源，转变教学与学习方式［1］.近年来，艺术生已成为高中生中的重要群体.由于艺术生数学基础普遍薄弱，同一个班数学成绩两极分化大，尤其在高三备考时期，容量大课时少，数学课上好学生吃不饱，薄弱生难跟上.基于此，广州市教育科学规划项目“‘O2O’教学模式在艺术生数学教学中的实践研究”课题组从学情出发，紧扣高三一轮复习课的“课前、课中、课后”三个重要节点，选取重要主题内容进行线上线下深度融合的教学实践与研究，经过两年努力，探索出“O2O”教学模式（Onlineto Offline即线上线下教学模式，以下简称“O2O”），它是将“线上教学”与“线下教学”两部分优势互补，通过网络思维解决教育问题，实现互联网技术与课堂教学相结合，体现人机交互、师生交互和生生交互的教学模式［2］，其实施流程如图1所示.

“O2O”由三个环节构成：

第一环节，课前线上自学.教师利用晚修在班级群布置课前线上任务.任务分两类：一类是基础知识回顾，教师针对薄弱生发布资源，学生通过资源观看学习，回顾相关基础知识；另一类是布置课前梯度任务单，教师发布调查问卷，学生在回顾知识后尝试完成，以便了解学情，更好地把握课堂的深度与广度.

第二环节，课中线下教学.课堂永远是教学的主阵地.课堂教学是突破重难点、解决自学疑惑的关键环节，更是学生认同并积极投入该模式学习的关键环节.教学中，先反馈线上自学情况，然后针对重点、难点，通过师生活动，完成课堂任务，及时小结反思，布置分层作业，提升学生数学素养，高效备考.

第三环节，课后线上巩固.根据线下课堂教学的情况，教师利用晚修或周末给学生推送微课.微课分两类：一类是基础型，主要回顾课堂的例题；另一类是提高型，是对课堂的拓展.学生在完成分层作业时，可根据自身情况选择并反复观看，到达及时巩固、强化的效果.

2 高三复习课教学设计

为确保研究的真实性、学术性、典型性，笔者以人教A版《普通高中教科书·数学》必修第二册（以下简称“教材”）“直线与平面垂直”复习课为例，呈现所任教高三年级的一次“O2O”模式下的一轮复习课及启示.

2.1 教学分析

（1）单元框架下垂直关系的内容分析

立体几何是高中数学的重要内容，是考查空间想象能力的重要载体.通过呈现常见的平面基本模型和空间几何模型，充分挖掘其结构特征以及位置关系与度量关系，是高考考查的重点.由于空间几何体的元素较多，联系较紧密，因此对线面垂直的考查，往往会涉及到其他平行或者垂直定理的渗透与综合，体现基础性和综合性.因此，立体几何的学习要突出和抓好对线面垂直的学习，这样才能更好地把握整个知识结构.如下图2反映了垂直与方方面面的联系.

（2）艺术生学情分析

艺术生的高三文化课一轮复习往往与艺考备考同步进行，这段时期学生对大部分的基础知识印象不深，尤其基础薄弱的学生，需反复学习才可唤醒记忆，而基础较好的学生，唤醒后只能完成一些简单任务.总体来说，备考时间往往不足.本课前学生已回顾“平行关系单元”，本课作为“垂直关系单元”的第一课时，内容重要，应由浅至深，由易到难，多设置思维引导点，以任务驱动引领学生分析问题和解决问题，注重前后知识的联系，完善数学认知结构.

（3）教学目标

根据《标准》对本单元的描述，确定本节复习课的教学目标如下：（1）掌握直线与平面垂直的定义和判定定理，渗透转化与化归思想；（2）能从模型特征的视角充分挖掘几何体中平面基本图形的性质以及度量关系，建立垂直关系，渗透平面化等转化与化归思想和强化模型意识.

（4）教学重点、难点

本课重点为归纳岀空间中垂直关系判定的核心及突破空间中垂直关系判定的核心问题，逐步形成解决问题的核心方法.难点为证明线面垂直要点的把握与提炼、核心经验的形成及在复杂问题中的应用.

2.2 教学过程

2.2.1 课前线上自学，师生资源交互

教师通过班级群，从国家中小学智慧教育平台、广州电视课堂、各大教育教学类网站及本课题组组建的校本资源库等，遴选合适的学习资源推送给学生，并下发学习任务单，供学生自主学习.

任务1：通过资源观看，回顾直线与平面垂直的判定定理.

任务2：请分别用文字语言、图形语言、符号语言，写出线面垂直的定义.

任务3：请分别用文字语言、图形语言、符号语言，写出直线与平面垂直的判定定理.

任务4：运用直线与平面垂直判定定理的关键是什么？

任务5：〔教材第162页习题8.6第（2）题〕设l，m，n均为直线，其中m，n在平面α内，则“l⊥α”是“l⊥m且l⊥n”的（ ）.

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

设计意图：通过问题驱动，引导学生构建知识框架，唤醒沉睡经验，为学生的活动经验从模糊变得清晰莫定基础.

任务6：已知四面体PABC中可能有①PA⊥AB，②PA⊥AC，③△ABC为某圆内接三角形且AB为直径，④PA⊥平面ABC，⑤BC⊥平面PAC.如图3，请以上述的一个或多个作为条件，一个作为结论，直接体现线面垂直的定义、直线与平面垂直的判定定理，并用语言表达该内容.

设计意图：开放性的问题情境设置，既可暴露学生思维的深度与存在的问题，又可让学生构建“线线垂直”与“线面垂直”关系的一维知识体系.

任务7：正方体中存在大量的线面垂直关系，请同学们参照试题1，改编或自编一道线面垂直的试题，需要包含答案，改编优良的试题将用于课堂教学环节.

试题1 （教材第171页复习参考题8·第12题）如图4，在正方体ABCD-A1B1C1D1中，证明：B1D⊥平面ACD1.

设计意图：通过编题，促使不同层次的学生得到各自不同创造力的发挥，教师从中选取备课资源，引起学生兴趣，激发学生对课堂的期待感.

2.2.2 课中线下教学，师生合作探究

线上反馈：通过资源观看，学生对定义、定理的单次应用还没熟练掌握，尤其书写格式不规范，对定理的多次使用存在障碍，没能抓住问题核心及基本思路方法.因此课中线下教学既要回归教材、整合资源，也要把握高考方向，采用并列式、递进式题组，给学生启发诱导，夯实基础，掌握重点，突破难点.

题组1

在正方体ABCD-A1B1C1D1中，完成下列问题：

（1）如图5，证明：B1B⊥AC；

（2）如图6，证明：B1D⊥AC；

（3）如图7，证明：AD1⊥平面A1B1D；

（4）如图8，证明：B1D⊥平面ACD1；

（5）如图9，若E，F分别为AC，BB1的中点，证明：EF⊥AC；

（6）如图10，若E为AC的中点，F为BB1上一点，证明：D1F⊥AC.

追问1：本题组呈现什么特点，目标指向什么？问题解决的关键是什么？所需条件如何挖掘？

设计意图：把教材习题、多位学生的编题整合为一个前后关联的问题串，注重引导学生书写规范和表达准确.其中第（5）问结合“EF∥B1D”或构造等腰三角形，一题多解，开拓思路，引导学生经历线线垂直在立体几何平面图形中是如何产生、挖掘和呈现的.

追问2：点F在运动过程中，保持着什么结构特征？同学们能归纳出什么数学模型？

设计意图：通过小组讨论，提炼第（6）问中的“D1-AC-F”结构，由两个等腰三角形拼接而成，并进行动态展示，给结构命一个通俗有趣的名字“鳄鱼的嘴巴”，如图11，学生用自然语言并结合鳄鱼的特征进行描述，生动形象，激发兴趣.

追问3：同学们能用符号语言描述此模型的特征吗？模型特征会受鳄鱼张开嘴巴大小的影响吗？

设计意图：引导学生规范严谨地书写，归纳出模型特征，挖掘模型中的垂直关系“BC⊥AD”，并对模型进行动态理解.

追问4：请对比试题2，同学们发现了什么？

试题2 （旧教材人教A版必修2第67页练习1）如图12，在三棱锥V-ABC中，VA=VC，AB=BC，证明：VB⊥AC.

设计意图：模型源于教材，在一轮复习中，要提高学生重视教材、回归教材的意识.

题组2

（1）（2017年全国卷Ⅲ）如图13，四面体ABCD中，△ABC是正三角形，AD=CD.证明：AC⊥BD.

（2）（2009年海南卷）如图14，在三棱锥P-ABC中，△PAB是等边三角形，∠PAC=∠PBC=90°.证明：AB⊥PC.

（3）（2013年全国卷Ⅰ）如图15，三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°.证明：AB⊥A1C.

追问1：上述问题有何特征？如何处理？

设计意图：题组2采用高考真题，聚焦“鳄鱼嘴巴”模型，进一步训练学生分析基本图形结构特征，上升到模型中来，强化模型意识，重点落实证明过程的规范性，暴露艺术生常见的书写、步骤等问题.

题组3

（1）（2011年新课标Ⅰ卷）如图16，四棱锥P-ABCD中，底面ABCD是平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD.证明：PA⊥BD.

（2）（2018年全国卷Ⅱ）如图17，在三棱锥P-ABC中，AB=BC=22，PA=PB=PC=AC=4，O为AC的中点.证明：PO⊥平面ABC.

设计意图：延续以上题组，多角度深挖基本图形结构中的垂直关系，其中本题组（1）的条件类似于题组2（3），却要用到余弦定理和勾股定理逆定理，渗透平面化思想；本题组（2）容易误导学生使用“鳄鱼嘴巴”模型，引导学生要从问题出发，结合边长等具体条件协同思考，切忌滥用模型.

小结思考：本节课你学习了什么？你是怎样学习的？

设计意图：学生发言，教师点评，提高学生学后反思的意识，深化对平面基本图形的位置关系、度量关系的认知与理解，渗透平面化等转化思想，强化模型意识，发展直观想象、逻辑推理等素养.

2.2.3 课后线上巩固，师生优化梳理

A组任务：如图18，在正方体ABCD-A1B1C1D1中，M，N，G，H分别是DD1，BC1，CD，AD的中点.证明：（1）MN∥平面ABCD；（2）MN⊥平面A1AG.

设计意图：继续采用课前线上环节学生自编的优秀题目作为课后A组作业，既能巩固直线与平面平行、直线与平面垂直判定定理的应用，又能让学生获得成就感，激发学生课后完成作业的投入度.

B组任务：（1）（教材第152页练习3）如图19，在直四棱柱A′B′C′D′-ABCD中，底面四边形ABCD满足什么条件时，A′C⊥B′D′.

（2）（2016年山东卷）在如图20所示的几何体中，D是AC的中点，EF∥DB，AB=BC，AE=EC，求证：AC⊥FB.

C组任务（选做）：请同学们从上述A，B组试题中，找出“面面垂直”关系，并给予证明.

设计意图：一轮复习B组作业既紧扣教材，又衔接高考，加深学生对本课内容的掌握.C组作业则给学有余力的学生进行拓展，为后续复习作铺垫.

课后的线上巩固环节中，教师根据学生的课堂练习与课后任务反馈的结果，及时整合相关微课进行推送，学生可通过课后微课的学习，从而突破本课的重点、难点及疑点，顺利达成教学目标.

3 总结与展望

结合《标准》的要求，教师要有意识地积累数学活动案例［1］，重视“实践性智慧”，借案例进行反思，高度重视案例（包括正例和反例）的分析，并能通过案例的比较获得关于如何从事新的实践活动的重要启示［3］.“O2O”是课题组结合艺术生高三备考现状，对新型教学模式的实践，普遍得到学生、家长的认可.它对培养学生形成独立的学习意识、促进全面发展有重要意义，但仍存在一些问题有待解决，如课前推送的资源没形成体系、课后微课的整合是否有效等.课题组将继续努力，对该模式是否适用于其他课型的推广，作进一步探究.

参考文献：

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［S］.北京：人民教育出版社，2020：83.

［2］宋昱莹.“O2O”教学模式在高中地理教学中的应用研究［D］.石家庄：河北师范大学，2017.

［3］郑毓信.课改背景下的数学教育研究［M］.上海：上海教育出版社，2012：109-111.