单元整体视域下初中勾股定理复习课的教学设计研究

于志游 莫鄯仟 童莉

［摘  要］ 《义务教育数学课程标准（2022年版）》强调“结构化整合学习内容，发展学生的核心素养”，单元复习课是结构化整合学习内容的重要途径之一，而以往的复习课重在知识讲解，轻视结构体现和素养发展. 文章以勾股定理复习课为例，主要探究了教学中存在的问题，从单元整体视域探讨了初中勾股定理复习课的设计思路，并根据设计思路进行了具体的教学设计，供教师参考.

［关键词］ 单元教学；勾股定理；教学设计；核心素养；几何直观

随着《义务教育数学课程标准（2022年版）》（下称新课标）的颁布，课程目标从知识本位时代过渡到素养本位时代，强调“结构化整合学习内容，发展学生的核心素养”［1］. 大单元教学跳出课时和单元的限制，对单元知识结构整体优化，从一堆知识中抽出一条线，串联零散的知识点. 大量研究表明［2］［3］［4］［5］，以大概念、大任务为导向的大单元整体教学成为落实核心素养的有效途径. 其中，单元复习课需要对整个单元的知识进行复习，是学生对单元数学知识“再认识”“再整合”“再提高”的契机. 而当前单元复习课还比较传统，没有很好地体现单元整合性和素养发展性的要求. 因此，本文结合北师大版八年级上册教材中的勾股定理单元复习课课例，探讨如何在单元整体视域下进行初中数学复习课教学设计.

初中勾股定理复习课教学的常见问题

勾股定理是初中数学的重要内容，位于北师大版八年级上册的第一个单元. 它从三边关系的角度进一步刻画了直角三角形的特征，是后续第二章实数内容中无理数学习的必要基础，是第三章位置与坐标内容中求两点间距离的理论基础，也与第五章的二元一次方程组息息相关，因此勾股定理是初中数学的重要内容之一，很多教学比赛中都会选择这部分内容作为重要选题. 勾股定理复习课是对勾股定理单元知识的“再认识”“再提高”，促使学生对知识结构优化整合、查漏补缺. 一般地，比赛课都是经过教师深入探究而形成的，可以代表该教师的最高水平，通过分析比赛课能更精确地找到教学中存在的主要问题. 因此，本文选择重庆市字水中学举办的初中数学第六届“卓越杯”教师技能大赛中，以“勾股定理单元复习课”为主题的两节课来做分析.

1. 课例简述

课例1  教师先通过思维导图的方式，分别按照边和角对三角形进行分类，类比等腰三角形研究路径梳理直角三角形相关知识点，引出勾股定理的概念. 之后以题带练，复习勾股定理和勾股逆定理的概念以及其应用，五道例题分别对应分类讨论、方程、数形结合、转化、数学建模等思想. 最后在小结环节总结一般研究路径：从特殊到一般，将未知转化为已知.

课例2  教师以一道求直角三角形边长的简单例题入手复习勾股定理的三种使用方法：直接求解、方程求解、构造直角求解，让学生先做后学，复习勾股定理及其逆定理. 接着分成四个板块依次讲解勾股定理与平面几何、解析几何、立体几何以及数系扩充等四个方面知识的联系，复习包括折叠问题、最短路径问题等经典题型. 最后在总结环节中引导学生构建知识网络、总结思想方法.

2. 问题梳理

两个课例无疑是经过精心打磨的课程，各有优点. 课例1运用思维导图梳理本章知识与前后章节知识的关系，注重思想的提升，有一定的大单元整体设计的意识；课例2在课程开始时就利用一道简单例题引导学生总结勾股定理的三种使用方法，注重方法的总结，并且例题选择有代表性，注重勾股定理与本学期所学的其他单元知识内容的整合应用. 但是这两个课例在体现单元整体视域时还存在以下两个问题.

问题1  对知识讲解与思想提升的权重把握不当. 单元复习课一般比较关注知识复习讲解和思想方法提升，这两部分要在整体结构视域下分配好合理的教学时间. 课例1过于注重思想提升. 课程为了得出几何图形的一般研究路径，一开始就花费了超过10分钟来构建思维导图，思维导图知识涵盖范围太广，详细讲述等腰三角形的定义、性质、判定等学生早已熟知的内容. 这导致后续例题讲解的时间不够. 同时没有提炼方法，直接从知识讲解一步跨越到提炼思想，学生上手较难. 与之相对应的课例2则过于注重知识讲解，偏重于复习经典题型及其求解方法，而这些在以前的课程中已经学习过了. 复习课不仅仅是经典题的再回顾，也不是理清知识点，而是让学生有新的收获［6］.

问题2  例题之间缺少关系. 单元复习课的另一个重点是巩固性例题的选择，在整体结构视域下需注意例题间的联系. 课例1是利用数学思想来链接例题，而数学思想之间的关联性其实不是很强，这就使得例题之间缺少联系，课程的连贯性大打折扣. 课例2是站在期末复习的角度设计课程，按照交叉单元之间的关系链接例题，单元之间联系紧密，但是每个单元中对应的例题之间的关联性不强. 可见，单一的思想或知识梳理不能很好地链接例题，还需要多一条线索来整合例题.

单元整体视域下初中数学的“勾股定理”复习课的设计思路

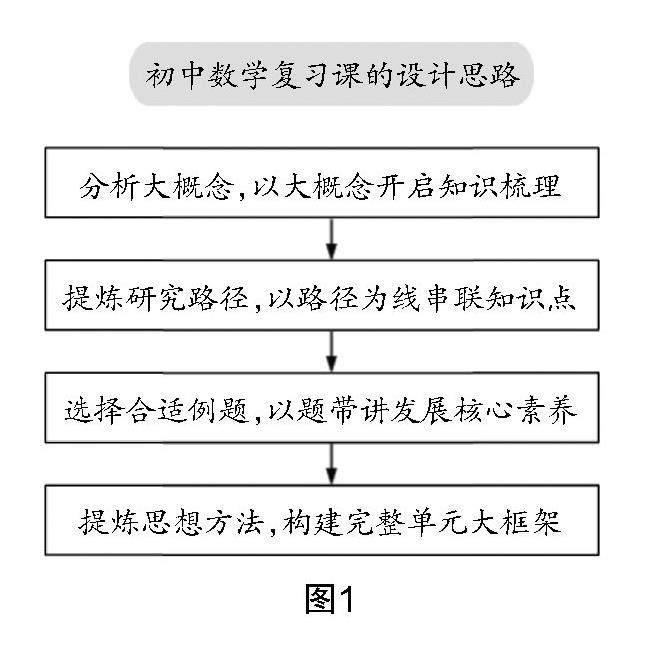
依据以上勾股定理复习课中常见的问题，以及聂静、罗振国提出的以大概念为中心的单元教学设计路径［7］，笔者给出单元整体视域下初中数学复习课的设计思路，如图1所示，共分为四个步骤：（1）分析出大概念，以大概念开启知识梳理；（2）提炼研究路径，以路径为线串联知识点；（3）选择合适例题，以题带讲发展核心素养；（4）提炼思想方法，构建完整单元大框架. 下面以北师大版初中勾股定理复习课为例讲解该设计思路.

1. 分析出大概念，以大概念开启知识梳理

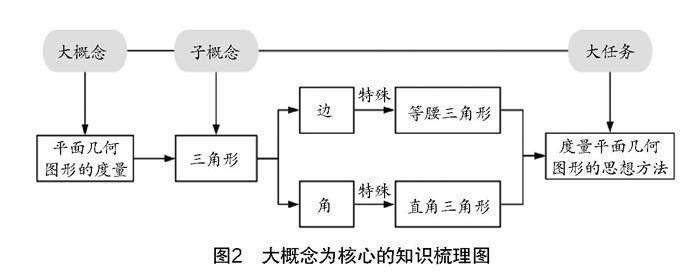
勾股定理是平面几何图形度量中三角形度量的最基本定理，通过研究教材，在数学知识的整体高度，确定勾股定理章节的大概念是平面几何图形的度量，相对应的大任务是掌握平面几何图形度量的相关思想方法并应用于实际.

以大概念梳理单元知识，需要梳理教材中与大概念相关的子概念. 显然勾股定理是平面几何图形度量在三角形这一子概念中的体现. 三角形可以按照边或角进行分类，选取特殊的三角形，包括等腰三角形以及直角三角形，作为研究对象，探究度量平面几何图形的方法.

2. 提炼研究路径，以路径为线串联知识点

对等腰三角形的研究，包括其定义、性质（等边对等角）、判定（等角对等边），总结基本研究路径是“定义—性质—判定”. 勾股定理章节的编写是按照“问题情境—建立模型—解释与应用拓展”的模式展开的，这是北师大版教材的惯用编写风格. 教科书的编写模式涵盖了直角三角形的性质、判定与应用. 综合以上两者研究路径，得出平面几何图形的一般研究路径是“定义—性质—判定—应用”. 该路径串联本章知识点，凸显本章在三角形这一大单元下的地位.

3. 选择合适例题，以题带讲发展核心素养

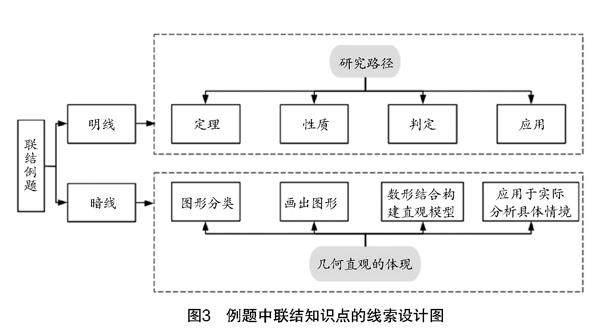
选择例题应该与研究路径相对应，将知识点连成线. 除了研究路径这一明线串联知识点外，还需要核心素养这一暗线. 新课标中，几何直观主要体现在四个方面［1］：（1）能够感知各种几何图形及其组成元素，依据图形的特征进行分类；（2）能够根据语言描述画出相应图形，分析图形的性质；（3）建立形与数的关系，构建数学问题的直观模型；（4）利用图表分析实际情境与数学问题，探索解决问题的思路. 因此，在选取例题时需要尽量体现上述四个方面，培养学生几何直观核心素养.

以题带讲更加符合初中生的思维习惯. 初中生正处于从形象思维中培养逻辑思维的学习阶段，其逻辑思维还不够成熟，对形象直观的讲解更为深刻. 因此，教师需注重直观呈现，讲解后点出知识点和思想方法，加深学生印象.

4. 提炼思想方法，构建完整单元大框架

思想方法是一节课的灵魂，提炼题目中有关平面几何图形度量的思想方法，完成本单元的大任务. 同时，也需要通过思想方法的提炼，构建单元大框架，但是单元大框架不能直接给出，应该由师生一起共同探究总结. 学生通过本章学习对直角三角形有了进一步认识和理解，联合等腰三角形的研究路径，将特殊三角形推广到一般三角形，为后续初中阶段的三角函数，以及高中阶段的一般三角形的性质和正弦、余弦定理的学习埋下伏笔.

单元整体视域下初中勾股定理复习课的教学设计

1. 情境引入，给出大概念

勾股定理是个古老的定理，不同的国家或者地区都曾独立发现过它. 古巴比伦人通过勾股数组来确定直角三角形，测量土地面积进行土地分配. 在我国的测量学著作《海岛算经》中就介绍了用勾股定理计算海岛高度的方法.

由上述例子，可以看出勾股定理在生活实际中通常有什么用处呢？

设计意图  引出本章的大概念为平面几何图形的度量，而勾股定理是常用于三角形度量的基本定理.

2. 知识梳理，提炼研究路径

问题1  勾股定理是有关三角形度量的基本定理，而三角形类型繁多，同学们能否按照不同的要素将三角形进行分类呢？

问题2  若按照边进行分类，其中较为特殊的是等腰三角形，大家知道其哪些知识点呢？我们研究这些知识点的路径是怎么样的？

问题3  若按照角进行分类，其中较为特殊的是直角三角形，类比等腰三角形的研究路径，同学们能否构建出直角三角形的研究路径呢？

设计意图  让学生类比等腰三角形的研究路径，得出直角三角形的研究路径，引出勾股定理的概念的同时，给出平面几何的一般研究路径：定义—性质—判定—应用. 从该路径出发安排后续例题，使得知识点串联起来，初步培养几何直观的第一个体现方面：能够感知各种几何图形及其组成元素，依据图形的特征进行分类.

3. 以题带练，提升思想素养

例1  （题型一：直角三角形知二求一）如图5，在△ABC中，AB=20，AD为BC边上的高，且AD=12，DC=9，求△ABC的周长.

变式1  将例1中“如图”去掉，其余条件不变，请问△ABC的周长怎么求？

变式2  能否判断△ABC是个什么三角形？

设计意图  复习勾股定理以及勾股定理逆定理，对应直角三角形研究路径中性质以及判定环节. 变式1体现了分类讨论思想. 引导学生画出图形，培养几何直观的第二个体现方面：能够根据语言描述画出相应图形，分析图形的性质.

例2  （题型二：图形翻折问题）在Rt△ABC中，∠C=90°，AB=10，AC=6，点D为BC上的一点，将△ACD沿AD折叠，使点C恰好落在AB上的点E处，求BD的长.

设计意图  经典题型——图形翻折问题，有多种解法：可用等面积法、两点间的距离公式以及勾股定理求解. 解题时需用字母代表边，用方程求解，并利用方程沟通代数和几何，体现方程思想，培养几何直观的第三个体现方面：建立形与数的关系，构建数学问题的直观模型.

例3  （题型三：最短路径问题）一个圆柱体盒子高为2 cm，周长为6 cm，一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点G处吃面包屑，你能帮蚂蚁设计一条最短的线路吗？蚂蚁要爬行的最短路程是多少呢？

设计意图  复习经典题型——最短路径问题，引导学生将立体图形转化为平面图形，由未知转化为已知，凸显转化思想，对应研究路径中的应用环节，培养几何直观的第四个体现方面：利用图表分析实际情境与数学问题，探索解决问题的思路.

例4  （题型四：生活实际应用）图7左图是一辆登高云梯消防车实物图，右图是其工作示意图，起重臂AB（单位：m）可伸缩，伸缩范围为10≤AB≤40，且起重臂AB可绕点A在一定范围内转动，张角∠CAB的范围为90°≤∠CAB≤150°，转动点A距离地面MN的高度AC=5 m. （参考数据：≈1.7）

（1）当起重臂AB的长度为20 m，张角为135°时，求云梯消防车最高点B距地面的高度（结果保留根号）；

（2）某栋楼高39 m，若该楼中有居民家突发险情，请问该消防车能否实施有效救援？请说明理由.

设计意图  构造直角三角形求边，将勾股定理应用于生活实际，培养几何直观的第四个体现方面.

4. 总结反思，构建完整单元大框架

（1）勾股定理这一章你学习到了什么知识？研究路径如何？

（2）对应路径讲解了哪些经典题型？本节课涉及什么数学思想方法？

（3）本章知识与前后单元之间是什么关系？

设计意图  总结度量平面几何图形的方法，完成单元大任务. 引导学生从特殊三角形的研究联想到一般三角形的研究，体现研究数学对象的一般思路是从特殊到一般.

结语

单元复习课不同于新课，学生对所讲内容已有一定认识. 若知识讲解与思想提升这座“天平”过于偏向知识讲解，使复习课变成习题课，学生会觉得课程索然无味. 若过于偏向思想提升，将知识讲解悬于高空，使复习课变成表演课，学生会听得似懂非懂. 对于如何平衡知识讲解与思想提升的关系，本研究提出了单元整体视域下初中勾股定理复习课整体设计思路. 将单元知识放在以大概念为起点构建的知识体系中，凸显知识之间的联系. 接着以研究路径和核心素养两条线串联数学知识与数学思想. 在总结阶段由本章知识推广到未来相关单元知识，构建完整的知识框架. 如此，学生既复习了知识也提升了数学思想.  当然，该设计思路是结合勾股定理复习课分析得出来的，能否推广到一般课程还需要进一步教学实践.

参考文献：

［1］中华人民共和国教育部.  义务教育数学课程标准（2022年版）［S］. 北京：北京师范大学出版社，2022.

［2］王磊，陈建明，杨博谛等.  回顾与启示：近四十年中国基础教育数学单元教学研究［J］.  数学教育学报，2023，32（04）：21-27.

［3］李大永，章红. 基于整体把握的运算主线下的“分数指数幂”教学［J］. 数学教育学报，2016，25（01）：61-66.

［4］张丹，于国文. “观念统领”的单元教学：促进学生的理解与迁移［J］. 课程·教材·教法，2020，40（05）：112-118.

［5］邵朝友，崔允漷. 指向核心素养的教学方案设计：大观念的视角［J］. 全球教育展望，2017，46（06）：11-19.

［6］浦丽俐. 大单元教学观下的章末复习课教学思考——以“直线与方程”为例［J］. 数学通报，2022，61（02）：22-27.

［7］聂静，罗振国. 基于学科大概念的高三数学复习课单元教学设计——以“向量”单元为例［J］. 新课程导学，2023（28）：79-86.

基金项目：重庆市教育学会第十届（2021—2023年）基础教育科研立项课题（XH2021B133）.

作者简介：于志游（1978—），本科学历，中学一级教师，从事初中数学教学工作，曾获江北区优秀教师，江北区教学能手，江北区初中讲题比赛一等奖.

通信作者：童莉（1976—），博士，教授，硕士生导师，从事数学教育测评、数学教师专业发展研究.