《分数的意义》教学中思维导图的应用

高晨

摘要：《义务教育数学课程标准（2022年版）》中强调，数的概念学习要遵循整体性、一致性、阶段性的原则。不同学段数的概念学习内容要相互关联，教学设计上要由浅入深，逐层递进。《分数的意义》一课的学习一方面要和学生以往学习自然数的方法联系起来，还要和以往学习的知识联系起来，进行知识的迁移及认知的同化。直观的思维导图能够帮助学生更好地理解分数概念的内涵和外延，同时对分数意义的理解更加深刻。

关键词：数的概念思维导图数形结合分数的产生分数的意义

数形结合不仅是一种重要的数学思想方法，还是一种很好的理解抽象概念的方法。思维导图可以将抽象的数学概念与形象直观的图形语言相结合，让相对复杂的分数意义概念简单化、具体化。《分数的意义》学习中融入思维导图，能帮助学生系统地理解核心概念，教师也能更合理地安排教学。

一、利用思维导图，分析教材内容

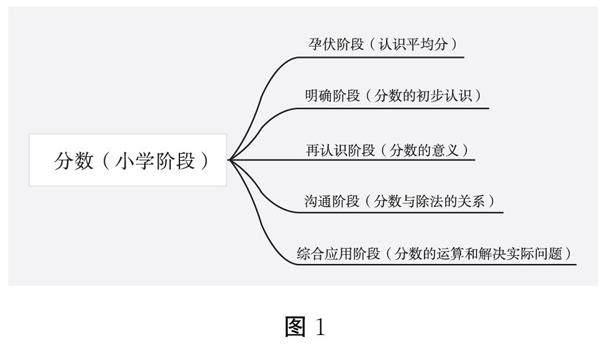
教师可以利用思维导图对分数知识进行梳理。分数的学习在小学阶段可分为孕伏阶段、明确阶段、再认识阶段、沟通阶段、综合应用阶段五个阶段。我们对现行苏教版教材进行了梳理，具体如图1所示。

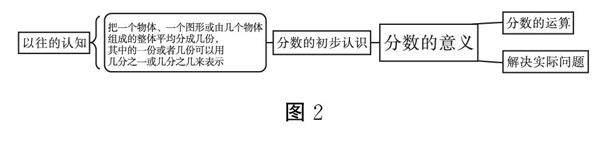
苏教版五年级《分数的意义》属于概念再认识，涉及的内容如下（图2）：

在《分数的意义》教学中，需要学生把握分数意义的本质。课前，教师利用思维导图分析教学内容，弄清分数前后知识脉络，方便教学从学生已有的知识储备出发，打通数学知识前后关联进行统筹。

二、利用思维导图，把握核心概念

《分数的意义》教学中，需要打破原有的对分数的初步认识，要从单位“1”的角度重新建立分数概念。单位“1”是一个不仅重要还抽象的核心概念。在学习过程中，学生很难判断出具体情境中哪个量是单位“1”。要想突破这个难点，教师需要在教学中引导学生理解分数的意义，掌握单位“1”的本质。

教学片段：

师：课前同学们也设计了一些分数，并画图展示了出来。我们一起来看一看，并请大家说一说自己的分数是什么意思。

师：说一说你的分数是什么意思？

学生回答。

师：在这块饼干中，他画的空白部分表示多少？表示这样的2份呢？

学生回答。（教师相机板书：分数）

师：这三个分数中，哪个是最基本的分数？

师：说一说你的分数。

学生回答。

师：每一份可以用哪个分数表示？空白部分呢？

学生回答。

师：哪个是最基本的分数？为什么？

学生回答。

师：这条一米的线段呢？

师：一起猜猜看老师会怎么提问？空白部分是多少？

师生一起回答。

师：哪个是最基本的分数？

师：这六个圆呢？

学生回答。

师：图中空白部分可以用哪个分数表示？其最基本的分数是多少？

（教师相机板书对应的分数，并且把最基本的分数写在相应分数的后面）

教师展示，提问：这四个同学都是把什么平均分？

师：你们都强调平均分，这里分别是把什么平均分？

师（提示）：1块饼干是一个物体。（贴教师相机板书：一个物体）那第二幅图呢？其他图呢？

生：一个图形。（教师相机板书：一个图形）

生：一个物体，一个图形，一个计量单位，一个整体。

师：真会概括。（教师在相应位置板书）

师：这里的一个物体，一个图形，一个计量单位，一个整体，都和哪个数有关？

生：都和数字1有关。（教师相机板书：1）

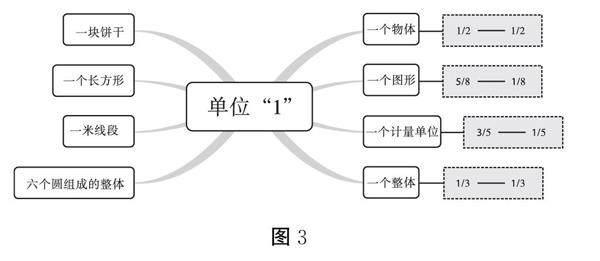
师：那这里“1”既可以表示一个物体，也可以表示多个物体组成的一个整体，在数学上我们称之为单位“1”（完善板书：单位“1”。在这里，利用思维导图板书对比，引发学生思考发现单位“1”和自然数1的不同，把握核心概念。）

通过单位“1”概念的学习，学生抽象思维水平得到提升，并对现实生活中和分数相应的数量关系有了进一步的理解和把握。学生通过本课《分数的意义》的学习，打通接下来探索分数与除法的关系、求一个数是另一个数的几分之几的方法的脉络，也为理解真分数与假分数的含义、分数的基本性质等内容提供了知识基础。

利用思维导图进行单位“1”的教学，帮助学生认识了单位“1”的内涵和外延，引导学生回顾已有自然数学习的经验，认识单位“1”和自然数1不同，引发学生认知冲突，从而为接下来抽象出分数的意义做铺垫，突出单位“1”的本质含义，学生在充分的探索与交流后拥有完整的思考空间。在认识分数的过程中，学生通过大量观察、推理和交流的活动机会，从具体情境中平均分不同物体得到分数，再回到分数意义的角度理解单位“1”，将抽象概念具体化。利用思维导图这种直观媒介，促使学生逐步加深对核心概念单位“1”以及分数意义的理解，符合相应学段学生的心理特征，有助于他们进行有效的思考，提高思维水平。

三、利用思维导图，确定核心问题

《分数的意义》教学不仅尝试探索分数的起源，也就是分数“为什么”产生的问题，还合理设置使学生理解单位“1”以及分数单位的意义，从而深入理解分数“是什么”。学生在经历分数概念的学习后，初步体会分数还可以用来表示部分与整体之间的关系。

教学中，教师利用思维导图呈现两个大问题（图4）。适当引导下，再设计出有一定思考空间的问题串。核心问题统领下，辅以问题串来推进数学学习的进程，既促进学生用数学的眼光发现问题，又推动学生用数学的方式思考问题。思维导图的呈现为接下来的探究提供方向指引。

教学片段：

师：今天我们要学习什么？

师：这个课题，它是一个概念的内容，你能提出哪些数学问题？

生：什么是分数？

师：真是有价值的问题。

生：什么是分数的意义？

生：为什么要学习分数的意义？

师：真会提问。

师：接下来我们就带着这两个大问题一起来学习本节课的内容。

分数的再认识，建立在概念认识基础上，最直接的方式就是让学生来提问，用学生的问题为接下来本课的学习内容奠定基础。对于概念性的内容，学生很容易想到分数“是什么”问题，也很好奇“为什么”要学习分数，这就是分数意义的学习中重要的两个内容。用思维导图呈现，为接下来本课的学习提供方向指引，课程最后，回归两个问题是否解决，形成闭环。

四、利用思维导图，启发学生思考

以往概念教学过度注重教科书上描述性知识的教授，导致学生对概念的掌握停留在文字表面上。关于概念的学习向内缺少方法，向外缺少方向，学生学习概念内容的创造性落实得还不够。教师应该引导学生从文字表象转向数学概念的本质，启发学生思考。把握分数意义概念的本质，也就是从单位“1”角度进行平均分，突出数学思考。

教学片段：

教师引导学生齐读单位“1”。

师：单位“1”是数量为1或者一个整体的统称。所以这里我们加了引号。

师：这里我们都是把什么看成单位“1”？

生：第一幅图是把一块饼干看成单位“1”。

师：你们自己画的分数是把什么看成单位“1”，和你的同桌说一说。

学生说一说。

师：刚刚一块饼干可以看成单位“1”，6个圆作为一个整体也可以看成单位“1”。（教师相机指着板书对应内容）生活中还有什么可以看成单位“1”进行平均分？

学生说一说。

师：说得完吗？数学上只用哪三个字就概括完了？

生：单位“1”。

师：这就是数学中的简洁美啊。

师：那你能用单位“1”说说这几个分数的意义吗？

学生分别说出四个分数（教师相机指导，用之前呈现的板书结合说明），说到第三个分数后教师小结：那下面的分数是不是也能这样说啊？

师：你能把这4句话概括成一句话吗？归纳一下什么是分数。（学生讨论）

学生回答。

师：谁有结果了，请试一试。

两位学生回答。

师：刚刚你们概括时都强调单位“1”平均分，你们的概括已经非常接近数学家的概括了，想不想看一看数学家是怎么表示的？

生：想。

共同总结：把单位“1”平均分成若干份，可以用分数表示其中一份或者几份的数。因为是平均分，所以我们说分数是将单位“1”平均分而来。（最后板书呈现的思维导图如图5）

学生通过之前的学习已经了解分数的各部分名称及分数的初步概念。什么是分数？分数是怎么产生的？分数有什么用途？这些是对分数的意义的深层追问，思维导图能帮我们有效指明这些问题的思考方向。学生在不停地思考中，发现新问题，感受解决问题的乐趣，加深对分数意义概念的本质的理解。

五、利用思维导图，感悟数学思想

数学思想是数学的灵魂，数学课堂上一定要有数学思想渗透。在本课中，涉及分类思想、集合思想、数形结合思想、一一对应思想、符号思想以及极限思想。从自然数到分数的引出，再到让学生体会分数与整数学习方式、认识方式的联系，让学生感悟分类思想和集合思想；通过数轴、思维导图让学生理解分数的产生还可以是累加得来，同时通过在数轴上找数，进一步感受数形结合、一一对应的思想；最后计数单位的细分，体现了极限思想。这些呈现的过程，教师捕捉，板书到黑板，串成思维导图，从而在教学过程中渗透数学思想。

教学片段：

师：在前面的学习中，我们知道整数都可以表示在数轴上。看这是1，两个1是2，三个1是3。这些数可以看成哪个数累加而成呢？

学生回答。

师：其实分数也可以。我们把0～1看成单位“1”，你能找到35的位置吗？

生：把0～1平均分成5份。

师：有几个这样的15？

师：那我们一起来数一数，1个15是多少？2个呢？3个呢？还能继续往下数吗？

生：5个15是55也就是1。

师：1里面有几个15？再加一个呢？6个是多少？

师：这些分数又是由哪个分数累加而成的呢？

生：是由15累加而成的。

师：随着分数单位的累加，分数不断变大。

回顾：我们是怎么找到35的位置的？

师：首先平均分，先找到15，像这样3个15就是35。以此类推，你能找到78的位置吗？它是由哪个分数累加而成的吗？

学生回答。

师：那910的位置呢？

学生回答。

师：它是由哪个分数累加而成的？

学生回答。

小结：在找这些分数的过程中，我们发现分数可以在数轴上找到与分数对应的点。

师：也就是说分数和点是对应的。

师：这里把单位“1”平均分成5份，中间数了几个分数？这里呢？平均分成8份，中间有7个分数；平均分成10份有9个分数[JP7]...[JP7]...随着单位“1”被平均分成的份数越多，找到的分数个数也就越多。继续分下去，分数的个数还将增多。

师：我们把目光回到这个分数。110还能用小数0.1表示。210就是0.2，710表示0.7。

师：这些小数又是由哪个小数累加而成？

生：0.1。

师：15，18，110这些分数单位就和整数的计数单位“1”，小数的计数单位“0.1”一样都是不断累加就能形成新的数。（用课件、板书呈现，使学生感受数的概念认识的一致性）

小结：前面的学习，一方面展示了分数单位的重要性，另一方面沟通了分数与整数和小数之间的联系。

运用思维导图呈现分数之间的联系，在数轴上将这些数罗列出来进行对比，把抽象的数学知识转化成学生易接受的直观知识。思维导图使得数学知识更加形象立体，有助于学生主动发现问题、提出问题，快速理解分析问题。思维导图可以很好地呈现概念教学中的对比环节，更是展示本课中数学思想与方法的有效途径。

在《分数的意义》教学中，课前，利用思维导图梳理教材内容，对前后知识进行串联，教师能够更好地把握本课的重难点。

课中，利用思维导图这种高效的结构化思考工具，及时捕捉学生提出的问题以及解决问题的过程，呈现课堂的架构，帮助学生厘清分数知识体系的脉络，更能将学生的灵感收集。我们的学生是面向未来、面向社会的学生，利用思维导图能帮助他们理解知识的呈现方式，感受知识的产生过程，丰富学生的学习资源，为学生自主学习创造条件，重塑更加有序的知识结构。课后，学生利用思维导图呈现课堂教学所学所获，有条理地整理相关内容，有助于学生自主学习。

总之，思维导图在《分数的意义》教学中的应用不仅有助于学生对知识的理解和记忆，还能培养学生的逻辑思维能力和创造性思维能力，是一种有效的学习概念的工具。

参考文献：

[1]吴正宪.小学数学教学基本概念解读[M].北京：教育科学出版社，2014.

[2]中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022.

[3]战娜.画图策略拨开概念教学的神秘面纱——“分数的意义”教学中的点滴启示[J].山东教育，2020（1/2）：7678.

责任编辑：赵潇晗

*本文系合肥市教研课题“思维导图在小学中年级数学概念教学中的应用研究”的研究成果，课题立项号为HJG22076。