结构化视角下的小学数学单元整体教学策略

周遵安

摘要：小学数学传统教学一般是以课时为单位进行设计的，课时之间内容关联度不够、整体性不强，导致学生学到的知识呈现碎片化的状态，影响了学生对知识的拓展和延伸。教师应准确把握教材整体结构，寻找知识之间的内在联系，将“零散”的知识结构化，让“隐藏”的联系显性化。教师可以关联、迁移和素养为抓手，从知识结构、学法结构和思维结构三个方面出发，实施结构化视角下的小学数学单元整体教学。

关键词：结构化；单元整体教学；数学核心素养

《义务教育数学课程标准（2022年版）》（以下通称“新课标”）指出：“改变过于注重以课时为单位的教学设计，推进单元整体教学设计，体现数学知识之间的内在逻辑关系，以及学习内容与核心素养表现的关联。”这需要教师立足学科的视角，对课程内容的基本结构以及主线脉络做到整体理解和把握，充分了解教材的自然单元在整个学科内容中的地位和作用，并在教学中加强与其他单元内容的联系，从而帮助学生有意义地建构和理解本单元知识，发展核心素养。结构化视角下的小学数学单元整体教学关注知识的联结、方法的迁移和思维的进阶，通过整体把握教学内容来建立结构关系。下面，笔者聚焦人教版小学数学教材“图形的认识与测量”主题的相关内容，谈谈结构化视角下的小学数学单元整体教学策略。

一、以关联为桥梁，建立知识结构

同一主题下的内容具有整体性和一致性，因此教师要将在同一主题下，但分布在不同学段、不同单元的内容进行整体分析、对比联系，从而提炼出核心概念。以核心概念为统领进行单元整体教学，有利于帮助学生理解知识之间的联系，将有共同本质特征的内容构成大单元或系列单元，建立完整的知识结构。

以人教版小学数学教材五年级下册第三单元“长方体和正方体”为例，从单元角度来看，“长方体和正方体”单元的教学内容主要由三部分组成：对长方体和正方体的认识、表面积的计算、体积的计算。其中，对长方体和正方体的认识是学习计算表面积和体积的基础，而计算表面积和体积的学习是从度量角度加深对图形特征的认识。

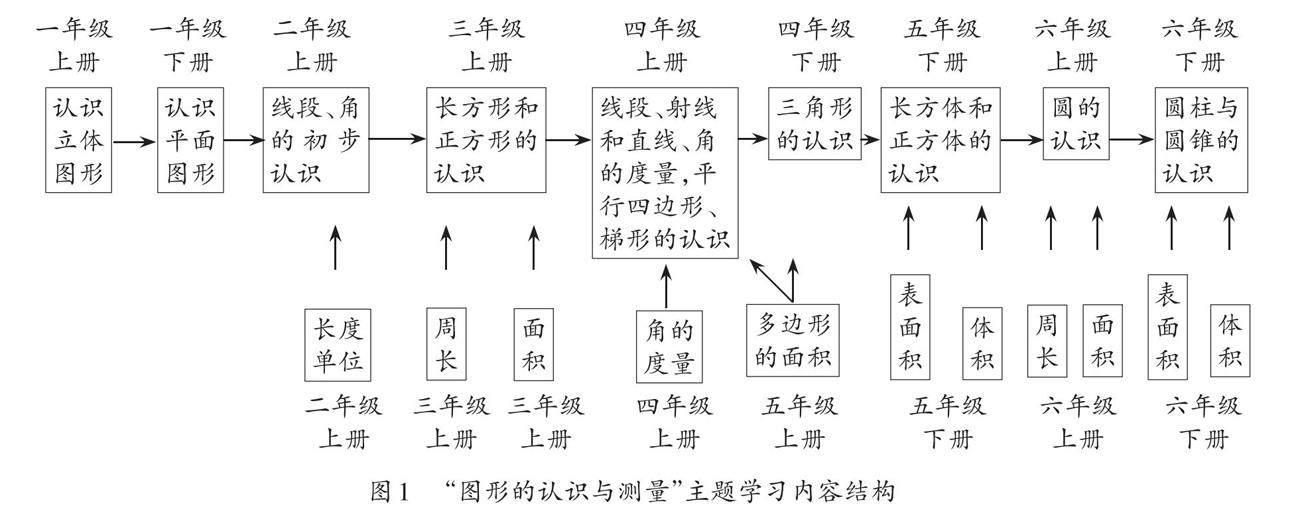
从“图形的认识与测量”主题视角来梳理，笔者将整体学习内容划分为图形的认识和测量两个支线（见图1）。

从“图形的认识”的学习进程中可以发现，在第一学段，学生已经对长方体和正方体有了初步的认识，能从实际物体中直观辨认长方体和正方体。第二学段的学习，主要是对平面图形的特征的探索，学生能够从点、线、角这些元素的角度来认识并刻画平面图形。第三学段转入立体图形特征的学习，在此阶段，学生从点、线、面这些元素的角度来认识并刻画立体图形，通过动手操作、观察想象等活动，建立起立体图形之间以及平面图形与立体图形之间的联系。不管是一维、二维、三维图形，认识图形特征时，都是从点、线、角、面的数量、大小及位置关系这三个维度进行研究。例如，三角形有3个顶点、3条线段和3个角；平行四边形有4个顶点、4条线段和4个角，对边相等且互相平行；长方体有8个顶点、12条棱，6个面，相对的棱长度相等，相对的面大小相等。

从“图形的测量”的学习进程中可以发现，整体呈现出一维—二维—三维的路径。从长度到面积再到体积的学习，是学生对空间的进一步认识。度量对象由一维的“线段”转变为二维的“面”再转变为三维的“体”，相应的度量单位由“线段”变为“正方形”再变为“正方体”，度量过程与方法也在进一步拓展。第一学段，通过对长度单位的认识，探索线段长度的度量，感悟到度量结果就是长度单位的累加。本阶段的学习是感悟度量本质的基石。第二学段，在探索长方形和正方形的面积时，教师要让学生感受到其本质是面积单位的累加。第三学段，认识体积单位，探索立体图形的体积度量，感悟度量结果是体积单位的累加。整体来看，图形度量的核心要素有度量对象、度量单位和单位个数。图形的度量本质上具有一致性，都是看度量对象包含了多少个度量单位。

“图形的认识与测量”主题的核心概念可以确定为“纬度”“图形的特征”及“度量单位”。教师可以围绕这些核心概念，将分散在不同学段、不同单元的内容进行整体梳理，构成系列单元，建立学习框架。例如，在探究图形特征时，教师可以判断其所属纬度，确定重点围绕哪些元素进行研究。在进行图形的测量时，教师可以度量单位为核心展开教学，这样有利于学生在进行新知的学习时，从整体上把握学习内容的结构特征，自主建立知识结构。

二、以迁移为纽带，形成学法结构

为了适应学生的思维特点，教材将知识内容按照螺旋式上升的顺序编排在不同的学段。虽然知识与知识之间具有相似性，但是在教学实践中仍然存在这些现象：学生在面对新知识时，往往无从下手，需要教师的多次引导才能解决问题；不能举一反三，学习能力较弱。为此，教师在教学中要积极创设真实、学生熟悉的情境，让学生自主探究，主动将学习方法进行迁移，从而顺利解决问题。这样的学习活动能帮助学生逐步形成学法结构、提升学习能力。

以人教版小学数学教材五年级上册第六单元“多边形的面积”为例，本单元的主要内容是平行四边形、三角形、梯形、组合图形、不规则图形的面积。教材突出的是转化思想，把未知图形转化为已知图形，寻找转化前后图形的联系，从而推导出计算公式或解决问题。而在此之前，学生已经积累了对长方形的面积推导的经验，通过摆一摆、数一数的方式，能发现“长方形的面积 = 每行面积单位的数量 × 行数”，并能根据每行面积单位的数量、行数与长、宽之间的对应关系，推导出“长方形的面积 = 长 × 宽”的结论。长方形的面积的推导，体现出了面积度量的本质，其实质就是计算该图形包含多少个面积单位。

在教学本单元内容时，面对新问题“平行四边形面积要如何计算”，教师可以引导学生先回顾长方形面积的推导过程，并出示学习任务：能否像长方形的面积推导那样推导出平行四边形的面积计算公式？学生自主探究，通过迁移长方形的面积的探究方法，借助方格纸或者小正方形等学具进行剪一剪、摆一摆，观察交流得出“平行四边形的面积 =每行面积单位的数量 × 行数”，并发现每行面积单位的数量、行数与平行四边形的底和高的关系，推导出“平行四边形的面积 = 底 × 高”的结论。在之后进行三角形和梯形的面积的教学时，教师设计同样的学习任务，给予学生充足的探究时间与空间，让学生通过方法的迁移，自主完成对三角形和梯形的转化，并通过寻找每行面积单位的数量和行数与三角形底和高，梯形的上底、下底和高之间的关系，推导出公式。整个单元的学习活动，学生都是基于度量的本质进行，通过“转化—找联系—推导公式—应用”的路径开展。在这样的学习路径里，学生能形成学法结构，也能为今后圆的面积、立体图形的表面积和体积的学习奠定基础。

三、以素养为目标，创造思维结构

核心素养的培养不是一节课就能完成的，它是一个长期累积的过程。教师不仅要能关注到教学内容与核心素养之间的关系，还要能关注到内容主线与核心素养发展之间的关系。这就要求教师立足单元整体，通过对整个主题、系列单元、课时数学知识和核心素养的主要表现进行分析，确定核心素养导向下的单元、课时教学目标，逐步培养学生的核心素养。

以长度单位相关内容为例，人教版数学教材将厘米和米的认识安排在第一学段，毫米、分米和千米的认识安排在第二学段。这5个课时的学习，都注重通过操作、体验和联系，引导学生建立长度单位的表象，积累度量的经验。为此，对长度单位内容进行教学时，教师要聚焦到对核心素养——量感的培养。结合以上教学内容以及量感的内涵，教师可以从不同角度去设计教学活动，丰富学生对量的感知，提升学生的数学思维。

在教学“厘米的认识”时，教师应注重经验的生成，让学生初步感知长度单位的产生过程，体会统一度量单位的重要性。在教学“米的认识”时，教师要注重让学生操作体验，经历观察、思考、测量等数学活动，初步感知针对真实情境要选择合适的度量单位，体会认识“米”的必要性。在教学“毫米的认识”时，这是学生第一次体会长度单位的细分，因此这节课要让学生感受单位间的联系，感悟到毫米精确性的价值。在教学“分米的认识”时，教师要注重让学生理解长度单位之间的十进制关系，帮助学生构建一个完整知识体系。由于千米是较大的单位，学生形成表象认识有一定困难，因此教师要注重培养学生的逻辑推理能力和估测能力，帮助其建立起表象认识。通过教学内容与核心素养发展的联系，确定好教学目标，可以让学生在丰富的活动中，发展量感，形成思维结构。

总之，在教学中教师不仅要关注教材的整体脉络及逻辑结构，还要关注学习的过程，要以核心素养为目标，通过关联、迁移等方式实施结构化的单元整体教学，使学生在丰富的知识背景中、在真实的探究过程中完善认知结构，从而助力核心素养的发展。

参考文献：

［1］马云鹏.基于结构化主题的单元整体教学：以小学数学学科为例［J］.教育研究，2023（2）.

［2］朱艳艳.指向结构化思维的小学数学单元整体教学探究［J］.江苏教育，2023（4）.

（责任编辑：杨强）