帕斯卡定理背景下圆锥曲线问题的命制与解答

唐宜钟 楚豪

【摘  要】  文章给出了帕斯卡定理及其退化形式、特殊情况和逆定理，并通过具体实例分析了帕斯卡定理背景下圆锥曲线问题的命制与解答.

【关键词】  帕斯卡定理；圆锥曲线；问题命制

近年来，高考要求“创新试题设计，加强关键能力考查，突出理性思维，发挥数学学科高考的选拔功能”［1］.遵循这一要求，2023年北京卷率先尝试以帕斯卡定理为背景进行圆锥曲线问题的命题.基于此，笔者尝试对帕斯卡定理背景下的圆锥曲线问题进行了挖掘.

1  帕斯卡定理

1.1  帕斯卡定理

图1帕斯卡定理于公元1639年为法国数学家布莱士·帕斯卡所发现，其描述为：如图1，设ABCDEF内接于圆（与顶点次序无关，即ABCDEF无需为凸六边形），直线AB与DE交于点X，直线CD与FA交于点Z，直线EF与BC交于点Y，则X，Y，Z三点共线．由射影几何的知识可知，将圆换成任意圆锥曲线，其结论依旧成立.

1.2  帕斯卡定理的退化形式

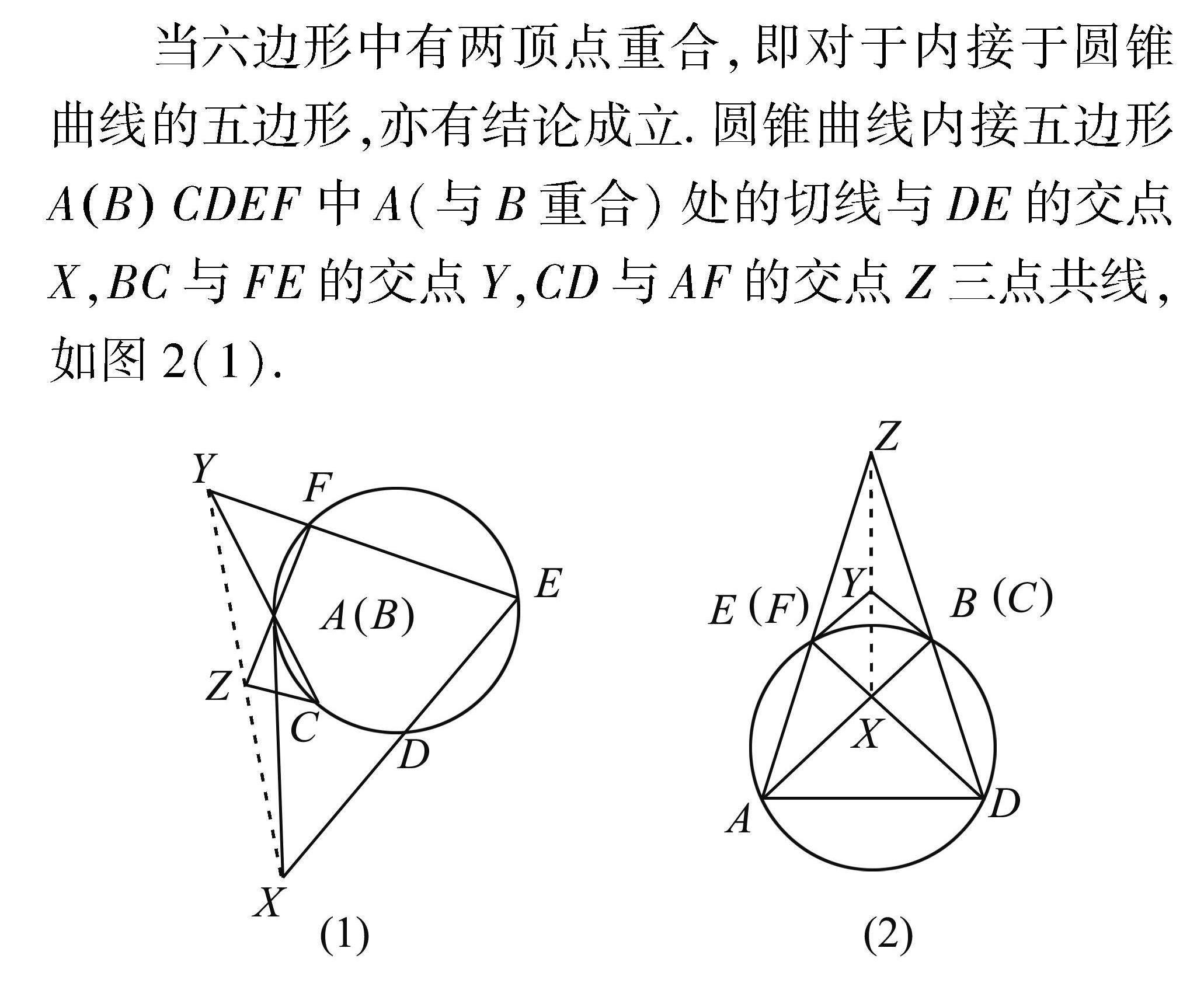
当六边形中有两顶点重合，即对于内接于圆锥曲线的五边形，亦有结论成立.圆锥曲线内接五边形ABCDEF中A（与B重合）处的切线与DE的交点X，BC与FE的交点Y，CD与AF的交点Z三点共线，如图2（1）．

图2

当六边形变为四边形ABCDEF或ABCDEF等时，如图2（2），（3），结论仍成立．当六边形变为三角形ABCDEF时，三组边AB，CD，EF变为点，如图2（4），

仍有结论成立．此时三点所共的线也称为莱莫恩线.

1.3  帕斯卡定理的特殊情况

我们将两条平行线认为交于无穷远处，则有以下结论：

①若圆锥曲线的内接六边形有且只有一组对边平行，则另外两组对边交点连线与平行对边平行.②若圆锥曲线的内接六边形有两组对边平行，则第三组对边也平行［2］.

1.4  帕斯卡逆定理

帕斯卡逆定理也成立.即如图1，设ABCDEF内接于圆（与顶点次序无关，即ABCDEF无需为凸六边形），直线AB与DE交于点X，直线EF与BC交于点Y，若直线CD与XY交于点Z，则点Z在直线FA上.

显然，帕斯卡定理中同时涉及到圆锥曲线中的点、直线、曲线等基本元素和斜率、定点、定线等基本表征.同时，对斜率、定点、定线的计算或证明又是解析几何的常见设问方式.因此，帕斯卡定理不失为圆锥曲线命题的一个良好背景.但考虑到图形的复杂程度、计算的繁杂性、解题的切入口等问题，以帕斯卡定理为背景的题目很少出现在公开的资料中.笔者从不同角度，原创、收集整理了一些相关问题，并对命题背景进行了探索.

直接使用圆锥曲线上的一个任意六点型，常规计算方法几乎是无法完成的.因此六点中的某些点需具有一定的特殊性，如简化横坐标或纵坐标，或者让坐标具有某种形式的对称性.使用左右或上下端点，或者使用一组关于原点对称的点，是常见的命题手段.

2  六点型

例1  已知双曲线Γ：x225-y216=1与x轴的左右交点分别为B，C.A，P为双曲线上不与B，C重合的不同两点，过P做双曲线Γ渐近线方向的平行线，分别交AB，AC于E，F，求证：EF过定点.

分析  如图3，由双曲线渐近线的性质，假设EP，FP交双曲线于无穷远处，交点分别记为S+∞，R+∞.由帕斯卡定理，AB∩PS+∞=E，AC∩PR+∞=F，则BR+∞∩CS+∞=T，且E，F，T三点共线.即过点B，C作渐近线方向的平行线BR，CS.显然它们交于定点T（0，4）.本题为一个双曲线中六点型的帕斯卡定理.除了选取左右顶点外，还选取了两个无穷远处的点.其常规解法如下：图3

由题可知，B（-5，0），C（5，0），由双曲线的参数方程，设A51+t211-t21，8t11-t21，P51+t221-t22，8t21-t22，则lAB：y=45t1（x+5），lEP：y-8t21-t22=-45x-51+t221-t22，联立解得E5t1t2-5t1+5t2+5（1+t1）（1-t2），8t1（1+t1）（1-t2）.又lAC：y=45t1（x-5），lFP：y-8t21-t22=45x-51+t221-t22，联立解得F5t1t2-5t1+5t2+5（1-t1）（1+t2），8t2（1-t1）（1+t2）.故kEF=yE-yFxE-xF=4t1t2+4t1+4t2-45t1t2-5t1+5t2+5，则lEF：y-8t1（1+t1）（1-t2）=4t1t2+4t1+4t2-45t1t2-5t1+5t2+5·x-5t1t2-5t1+5t2+5（1+t1）（1-t2）.由对称性易知，定点在y轴上，令x=0得，y=-4t1t2+4t1+4t2-45t1t2-5t1+5t2+5·5t1t2-5t1+5t2+5（1+t1）（1-t2）+8t1（1+t1）（1-t2）=-4t1t2+4t1-4t2+4（1+t1）（1-t2）=4，故定点为（0，4）.

3  五点型

更近一步的，让其中某两个点重合，把图形退化为一个五点型，以使得常规手段可以计算.

例2  （2023年北京卷）椭圆E：x2a2+y2b2=1（a>b>0），离心率e=53，点A，C分别为E的上下顶点，点B，D分别为E的左右顶点，|AC|=4.

（1）求椭圆E的解析式；

（2）点P为第一象限内椭圆上的一个动点，直线PD與BC交于点M，直线PA与直线y=-2交于点N.求证：MN∥CD.

解  （1）x29+y24=1；

图4

（2）如图4，本题选用了上下左右四个顶点.记lCC表示点C处的切线，即直线y=-2.对椭圆的内接六边形APDCCB，有AP∩lCC=N，PD∩BC=M，CD∩AB=T+∞（T+∞表示两条平行直线交于无穷远处）.由帕斯卡定理得M，N，T+∞三点共线，进而MN∥CD.

利用帕斯卡定理1.3的特殊情况，本题设问变为了证明两直线平行.而在常规计算中，平行的转化手段为斜率或者向量.其常规解法为：

设P（m，n），点P在椭圆上，则4m2+9n2=36.又D（3，0），则lPD：y=nm-3（x-3）.由B（-3，0），C（0，-2）得：lBC：y=-23x-2.联立两直线解得M3（-2m+3n+6）3n+2m-6，-12n3n+2m-6.又A（0，2），则lAP：y=n-2mx+2，与y=-2联立得N4m2-n，-2.故kMN=-12n3n+2m-6+23（-2m+3n+6）3n+2m-6-4m2-n=6n2-4mn+8m-24-9n2-8m2-6mn+12m+36.将4m2=36-9n2代入可得，kMN=23.又kCD=23，故MN∥CD.

例3  已知椭圆C：x2a2+y2b2=1（a>b>0）的离心率为23，且7，103为C上的一点.

（1）求C的标准方程；

（2）点A，B分别为C的左、右顶点，M，N为C上异于A，B的两点，直线MN不与坐标轴平行且不过坐标原点O，点M关于原点O的对称点为M′，若直线AM′与直线BN相交于点P，直线OP与直线MN相交于点Q.证明：点Q在定直线上.

解  （1）x29+y25=1；

图5（2）如图5，AB∩MM′=O，AM′∩BN=P，

O，P，Q三点共线，由帕斯卡逆定理可知，点Q为直线MN与lAA（椭圆在点A处的切线）的交点，即Q在直线lAA：x=-3上.本题是一个定线问题，结合帕斯卡逆定理，将其中四个点设置为左右端点和一组对称点，将定线设置为左端点的切线，使得本题常规计算变成可能.常规解答如下：

由题可知A（-3，0），B（3，0），设M（x1，y1），N（x2，y2），则M′（-x1，-y1）.设lMN：x=my+n，联立x=my+n，x29+y25=1，消去x得，5m2+9y2+10mny+5n2-9=0，y1+y2=-10mn5m2+9，y1y2=5（n2-9）5m2+9.又易得，lAM′：y=y1x1-3（x+3），lBN：y=y2x2-3（x-3）.由点P为直线AM′和BN的交点得，x1-3y1·yP=xP+3，x2-3y2·yP=xP-3，两式相加可得，2xP=x1-3y1+x2-3y2yP.化简得，xP=3mn+3yP，故lOP：x=3mn+3y.由图像的对称性知lOP与lMN的交点在一条垂直于x轴的直线上，联立lOP与lMN得，x=3mn+3y，x=my+n，消去y得，xQ=-3.因此点Q在定直线x=-3上.

4  四点型

让其中的两组点重合，就可将问题转化为四点型帕斯卡定理.

例4  椭圆C：x2a2+y2b2=1（a>b>0）的离心率e=32，a+b=3.

（1）求椭圆C的方程；

（2）如图6，A，B，D是椭圆C的顶点，P是椭圆C上除顶点外的第一象限内一点，直线DP交x轴于点N，直线AD交BP于点M.求证：直线MN过定点.

解  （1）x24+y2=1；

图6

（2）如图6，AD∩BP=M，AB∩DP=N，lDD∩lBB=T，由帕斯卡定理，点T在直线MN上.本题选用上顶点和左顶点，使得切线交点容易被找到.其常规解法为先设出lBP：y=k（x-2），联立lBP与椭圆，计算出P8k2-21+4k2，-4k1+4k2，进而得lDP：y=-2k+12（2k-1）x+1，N2（2k-1）2k+1，0.联立lBP与lAD得到M4k+22k-1，4k2k-1.利用M，N两点坐标得出lMN：y=2k+14x-2（2k-1）2k+1，进而得到定点T（2，1）（此处具体解答过程从略）.

5  三点型

例5  已知O为坐标原点，抛物线Γ：x2=4y上不同的两点A（4，4），Bb，b24（b≠0）.过A，B两点做Γ的切线交BO，AO于点M，N.直线MN交x轴于点T（t，0）.当∠AOB为钝角时，求实数t的取值范围.图7

解  如图7，显然x轴为抛物线在点O处的切线，lAA∩BO=M，lBB∩AO=N，M，N，T三点共线，由帕斯卡逆定理知：lOO∩AB=T.显然，当b∈（-4，0）时，∠AOB为钝角.对应的，t∈（-∞，0）.本题中，直线MN为△ABO的莱莫恩线.其常规解法如下：

由y=x24得y′=12x，故kAM=2，进而lAM：y=2x-4.又lOB：y=b4x.联立lAM与lOB得，y=2x-4，y=b4x，x=168-b，y=4b8-b，即M168-b，4b8-b.同理，lBN：y=b2x-b24，lOA：y=x.联立lBN与lOA得，y=b2x-b24，y=x，x=b22b-4，y=b22b-4，即Nb22b-4，b22b-4.故TM=168-b-t，4b8-b，TN=b22b-4-t，b22b-4.由TM∥TN得，168-b-t·b22b-4=b22b-4-t·4b8-b，化简得，t=4bb+4=4-16b+4.又当b∈（-4，0）时，∠AOB为钝角.故t∈（-∞，0）.

通过上述例证不难发现，以帕斯卡定理为背景的圆锥曲线问题，立足点、直线、圆锥曲线、平行等基础知识，充分调度直曲相交、韦达定理、切线求解等基本技能，突出对逻辑推理和数学运算等核心素养的考查.题设丰富，蕴含了圆锥曲线中最常见的定点、定值、定线、范围、证明等问题.兼顾技巧，如例1中通过观察图象的对称性使得定点简化，例3中通过合理求解规避非对称韦达等.在高考强调“反套路、反机械刷题，突出强调对基础知识和基本概念的深入理解和灵活掌握，注重考查学科知识的综合应用能力，落实中国高考评价体系中‘四翼的考查要求”［1］的今天，帕斯卡定理是一座亟待开发的宝库.

参考文献

［1］  教育部教育考试院.深入考查基础知识和能力  助力人才选拔和“双减”落地：2023年高考数学全国卷试题评析［J］.中国考试，2023（07）：15-21.

［2］  罗碎海，罗家平，麻红雷.帕斯卡定理的初等证明与高考题［J］.中学数学研究，2023（07）：17-20.

作者简介  唐宜钟（1988—），男，陕西汉中人，中學一级教师；主要从事高中数学教学和竞赛培训工作.

楚豪（1996—），男，陕西汉中人，中学二级教师；主要从事高中数学教学和竞赛培训工作.