7道原创高考数学新定义模拟题

基金项目  北京市教育学会“十三五”教育科研滚动立项课题“数学文化与高考研究”（FT2017GD003）.

【摘  要】  从教育部考试院于2024年1月组织的适应性考试反映的信息来看，新定义题将在数学高考试题中以重要角色出现：情景新颖、思维强度大、创新性强、分值高，甚至可能会以全卷压轴题的形式出现.文章首次发表的7道原创高考数学新定义模拟题就是深入领会高考改革方向，做好高三教学和复习备考的举措.

【关键词】  原创；高考；改革方向；数学；新定义；模拟题

2024年，吉林等6省及广西壮族自治区首次实施“3+1+2”新高考模式，1月19—21日由教育部考试院组织适应性考试，语文、数学、英语三科由教育部统一命题.这次测试，数学试题（下简称测试卷）的改革力度最大，主要包括下面四点：

（1）题量全面减少：由现行的22道左右减少到19道（较以前的多选题、填空题、解答题各减少了一道）.

（2）试题情境创新：比如复数题以往多是放在选填题中靠前的位置，但在测试卷放到了选择题第10题，特别是改变了以往复数问题的考查方法.

（3）思维强度增加：尤其是第19题（整个测试卷压轴题），这道新定义题情境新颖，思维强度提高.全部解答过程没有繁杂的数值计算，着重于对新定义的理解，利用新符号的推理过程，通过设问展现思维过程，考查推理能力.

（4）难度结构调整：以往的高考试题会设置三、四个坡度的难度，但测试卷基本上是一个坡度的难度，即所有的单选题、多选题、填空题的难度都比较平缓，只在解答题中设置了两道难度大的题目，体现了区分和选拔的功能.

测试卷的命题风格、试卷布局、难度结构代表了高考改革的方向，将在2024年及以后的新高考中全面体现.在中学（包括初中与高中）教学和复习中应高度关注［1］.

为了切实有效地提高高三复习备考质量，笔者编拟了7道原创高考数学新定义模拟题（它们均是首次发表），供有需要的读者选用.

北京高考数学卷从2002年开始自主命题，其鲜明特色就是新定义题居多，在选择题、填空题、解答题的压轴题中体现得最为明显.实际上，在高中数学的各个知识板块、各种考试题型（还包括数学文化试题［2］、劣构试题等）中均出现了大量的新定义题.

这次编拟的7道模拟题题目文字量大、信息量多、设问数量多、情境复杂、背景深刻（2006年高考福建卷理科第12题及2014年高考福建卷文科第12题、2010年高考广东卷理科第21题这三道新定义题的背景都是方格几何学［3］.方格几何学是由生于俄国的著名德籍数学家闵可夫斯基（Hermann Minkowski，1864—1909）最先开始研究的）；这7道模拟题的解答难度较大且复杂（为了突出试题的研究性及其完整性、创新性，会出现一题多解、设问数量较多的情形），为了避免解答冗长，可能会在题末给出解答时可使用的参考结论.为了使读者深入理解这些题目的科学性与严谨性，还会标注相应的参考文献.

这7道原创高考数学新定义模拟题的最大特点是研究性，所以其中大部分题目并不适合直接放到当前的数学试卷中使用（主要原因是解答时需要大量时间，而现在的高考时间是极为有限的2h），但可以先把每道题拆分成几道题（可先选择原题多个设问中的部分作为待求解的问题，再在题设中选择与待求解的问题相关的题设，这样就得到了一道简单些的新题），再选择其中的某道题作为考试题.另外，把这些新定义模拟题作为考试题时，所有的参考文献均可删去并且删去后不会影响考生理解题意和作答.

题1  公历又称阳历，就是我们平常所说的公元某年某月某日.公历一年的时间是地球绕太阳公转一周所需要的时间，大约是365.242 198 78天，合365天5时48分46秒.为了使一年的时间是整数天，就规定平年365天，闰年366天.公元年份能被4整除的是闰年，但世纪年（指能100整除的年份）要能被400整除的才是闰年，其余的年份均是平年.每年包括12个月，从前到后依次是1月，2月，……，12月，其中1，3，5，7，8，10，12月均月大，每月31天；4，6，9，11月均月小，每月30天；平年的2月28天，闰年的2月29天.

由以上平年及闰年的设置方法可知，任意连续的400年中共设置了97个闰年，共365×400+97=146 097天，平均每年为365.2425天，比实际的一年仅长约0.0003天，需积三千多年才多出一天.

农历又称阴历，是根据朔望月（即月球绕地球旋转一周的时间，大约为29.5306天）安排大月（30天）和小月（29天），力求使农历的平均每个月的时间近似等于朔望月，又根据公历一年相当的朔望月数安排农历的平年和闰年：平年12个月，闰年13个月.农历既保证了每个月初一是朔（看不见月亮），十五是望（月圆），又保证了农历一年的平均时间近似等于公历一年的时间.

农历平年的时间为29.5306×12=354.3672天，即354天或355天；农历闰年的时间为29.5306×13=383.8978天，即383天或384天.因为公历一年为365天或366天，所以公历的一年比农历的平年多10—12天，比农历的闰年少17—19天.

在我国的二十四节气（春雨惊春清谷天，夏满芒夏暑相连，秋处露秋寒霜降，冬雪雪冬小大寒）中，单数的叫节气，双数的叫中气，并按中气的顺序确定月序，如第一个中气是雨水，则有雨水的月就是正月，第二个中气是春分，则有春分的月就是二月.二十四节气的公历日期是比较稳定的，如雨水是2月18—20日，春分是3月20—22日，夏至是6月21—22日等等［4］.

明白了以上兩种历法，再来推算春节（即农历正月初一）的公历日期范围就不难了.

上面已经谈到，有雨水的月是正月，但雨水在正月的哪一天是不固定的，雨水可以是正月中的任意一天.所以公历最早的春节是月日，公历最晚的春节是月日.

解  1，20；2，20.解答过程见文［4］.

题2  设m（m≥2）是已知的正整数，数列an的项数至少是m+1.若数列an的任意连续m项之和都是常数D，则称这个数列为m-等和数列，常数D为这个m-等和数列的公和，并把2-等和数列简称等和数列；若数列an的任意连续m项之积都是常数J，则称这个数列为m-等积数列，常数J为这个m-等积数列的公积，并把2-等积数列简称等积数列.给出下列四个结论：

①常数列是等和数列，也是等积数列；

②等和数列与等积数列均是最小正周期为1或2的周期数列；

③若无穷数列an是等和数列，则an=12［D+（D-2a1）（-1）n］（n∈N*）；

④若无穷数列an是等和数列，则an=12［D+（2a1-D）cosnπ］（n∈N*）;

⑤项数与公和均是2024且各项均是自然数的等和数列共有2024个；

⑥公积是2024且各项均是自然数的等积数列共有16个；

⑦公和是2024且各项均是自然数的10-等和数列共有C102034个；

⑧公积是2024且各项均是正偶数的3-等积数列共有6个.

其中所有正确结论的序号是.

简解  ①③⑥.⑧错误：若数列an是3-等积数列且公积是2024，则可得an是以3为一个周期的周期数列.

设ai=2bi（bi∈N*;i=1，2，3），可得公积a1a2a3=23b1b2b3=2024，所以b1b2b3=1·11·23（b1，b2，b3∈N*）.可得该方程解的组数是9（其中恰有两个未知数取1的解的组数是3，恰有一个未知数取1的解的组数是3！=6），所以公积是2024且各项均是正偶数的3-等积数列共有9个.

题3  人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律，可以为制定一系列相关政策提供依据.早在1798年，英国经济学家马尔萨斯（T.R.Malthus，1766—1834）就提出了自然状态下的人口增长模型y=y0ert，其中t表示人口增长经过的时间（单位：年），y0表示起初即t=0时的人口数，r表示人口的年平均增长率，y表示人口增长t年后的人口数．

（1）由国家统计局网站公布的数据知，我国1950年末、1959年末的人口总数分别为55 196万和67 207万.根据这些数据，用马尔萨斯人口增长模型建立我国在1950—1959年期间的具体人口增长模型（答案中的数据要求保留六位小数）.

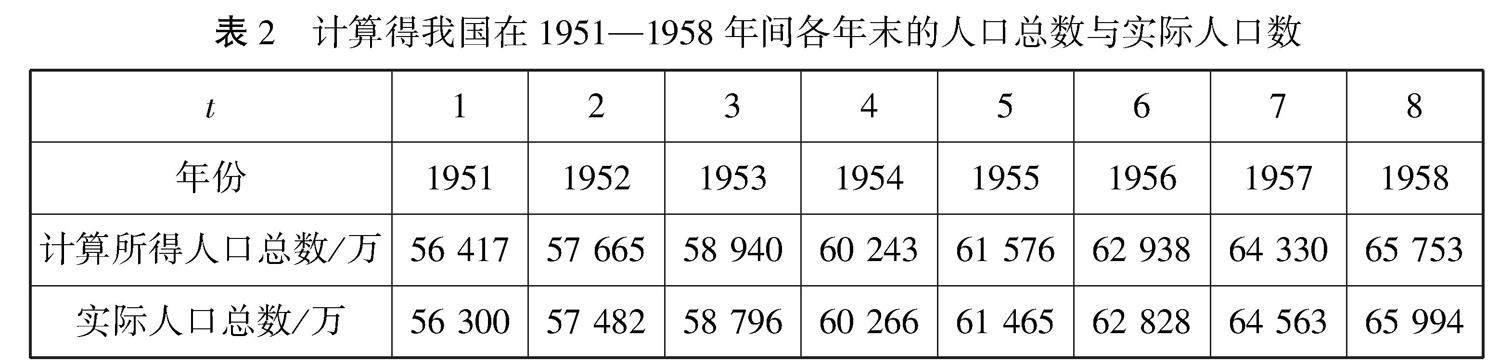
（2）利用（1）中的模型计算1951—1958年各年末的人口总数.查阅国家统计局网站公布的我国在1951—1958年间各年末的实际人口总数，检验所得模型与实际人口数据是否相符（计算人口数时答案保留到万人，说出检验思路即可）.

（3）以（1）中的模型作预测，大约在什么时候我国人口总数达到13亿（答案精确到1年）？

（4）事实上，我国1990年末的人口数为11.43亿，直到2005年才突破13亿.对由函数模型所得的结果与实际情况不符，你有何看法？

附参考数据：

我国在1951—1958年期间各年末的实际人口总数如表1：

67 207÷55 196=1.217 606…，55 196÷67 207=0.821 283…，ln1.217 606=0.196 886…，

ln0.821 283=-0.196 886…，130 000÷55 196=2.355 243…，55 196÷130 000=0.424 584…，

ln2.355 243=0.856 643…，ln0.424 584=-0.856 643…，0.856 643÷0.021 876=39.159 076…，

130 000÷39.159 076=3319.792 326…，39.159 076÷13=3.012 236….

解  （1）记1950年末为t=0时的情形，则1959年末是t=9时的情形，由题设可得y0=55 196，67 207=55 196e9r.

由所给的参考数据，可解得r≈0.021 876.

因而我国在1950—1959年期间的具体人口增长模型是函数y=55 196e0.021 876t（0≤t≤9），其中t表示人口增长经过的时间（单位：年），y表示人口增长t年后的人口数.

（2）用第（1）问得到的函数解析式及函数计算器可计算出我国在1951—1958年间各年末的人口总数，得到表2：

計算所得人口总数/万56 41757 66558 94060 24361 57662 93864 33065 753实际人口总数/万56 30057 48258 79660 26661 46562 82864 56365 994

如图1所示，在平面直角坐标系tOy中作出1950—1959年各年末计算所得人口总数的散点图，再作出函数y=55 196e0.021 876t（0≤t≤9）的图象：

图1

若散点图中的点基本上都在所作的函数图象上，则所得模型与实际人口数据相符；否则，所得模型与实际人口数据不相符.（注：实际的结果是相符.）

（3）设从1950年末经过x年我国人口总数达到13亿，由（1）中的模型可得

130 000=55 196e0.021 876x，

由所给的参考数据，可解得x≈39.159 076.

由进一法取近似数可知，大约经过40年即在1990年我国人口总数达到13亿.

（4）因为我国人口基数较大，人口增长过快，与我国经济发展水平产生了较大矛盾，所以我国从20世纪70年代逐步实施了计划生育政策.因此这一阶段的人口增长条件不符合马尔萨斯人口增长模型的条件，自然就出现了依模型得到的结果与实际不符的情况.

题4  （1）已知函数f（x）=b2a2x2-b2（x≥a）及直线l：y=bax，其中a，b是已知的正数.设函数f（x）图象G上的动点M（t，f（t））（t≥a）到直线l的距离是g（t），求证：

（i）图象G在直线l的下方；

（ii）用减函数的定义证明g（t）是减函数；

（iii）ε>0，存在常数α≥a，使得当t>α时，g（t）<ε.

（2）如图2所示，当曲线Γ上的动点M沿着曲线Γ无限远移时，若动点M到某直线l的距离无限趋近于0，则称直线l是曲线Γ的一条渐近线［5］.

图2

求证：直线y=bax是曲线y=b2a2x2-b2（x≥a>0，b>0）的渐近线.

鉴于篇幅，过程略，请读者自解.

注  （1）本题是由平面解析几何中的结论“双曲线x2a2-y2b2=1有且仅有两条渐近线，且这两条渐近线的方程分别是y=bax与y=-bax”编拟的一道函数原创题，该题及其解法对双曲线渐近线的教学也有指导意义.读者还容易给出本题第（1）问的三角换元证法.

（2）本题第（2）问结论的证明不能仅由直观感知得到，须“从浪漫到精确再到综合”，因而其本质就是证明第（1）问的诸结论.

（3）读者还可思考：如何证明“除y=bax外的直线均不是曲线Γ：y=b2a2x2-b2（x≥a）的渐近线”？

题5  把集合1，2，…，n的所有k（k≤n;k，n∈N*）元子集a1，a2，…，ak的全部元素乘积之和记作∑1≤ai≤na1a2…ak（其中i=1，2，…，k;a1，a2，…，ak两两不等，下同），在不发生混淆时也可简记为∑a1a2…ak.和式∑1≤ai≤na1a2…ak有如下性质：当2≤k≤n;k，n∈N*时，

∑1≤ai≤na1a2…ak=∑1≤ai≤n-1a1a2…ak+n∑1≤ai≤n-1a1a2…ak-1.

再把和式∑1≤ai≤na1a2…ak记作Gkn（k=1，2，…，n;k，n∈N*），又补充定义G0n=1（n∈N*）.

（1）用记号Gkn表示∏ni=1（x+i）即（x+1）（x+2）…（x+n）（n∈N*）的展开式；

（2）写出Gkn的类似于二项展开式系数性质Cm+1n+1=Cmn+Cm+1n的性质并给予证明；

（3）写出Gkn的类似于杨辉三角的Gkn三角（只写出前五行）；

（4）求证：若n≥2，n∈N*，则n是质数的充要条件是nGn-1n+1（指Gn-1n+1是n的倍数）.

解答本题时可使用参考结论：（威尔逊（Wilson）质数定理［6］）p是质数p（p-1）！+1.

过程略，请读者自解.

题6  对于直线l上两两互异的三个点A，B，P，若该直线上异于点P的另一点Q满足PAPB=QAQB（由本题末的参考结论可知，点Q由三点A，B，P唯一确定），则四点A，B，P，Q叫做一组调和点列.

设两个互异的动点A，B均在定曲线C：x2a2+y2b2=1上，定点P（x0，y0）（x0+y0≠0，x02a2+y02b2≠1）在动直线AB上.已知四点A，B，P，Q是一组调和点列.

（1）求证：动点Q在某条定直线上；

（2）求动点Q的轨迹方程.

参考结论：设两两互异的四个定点A，B，M，P（其中M是线段AB的中点）均在定直线l上，则在直线l上存在唯一的异于点P，M的点Q使得PAPB=QAQB，且：

（1）当点P在线段AB的反向延长线上运动时，点Q的轨迹是线段AM（但不是端点）；

（2）当点P在线段AM（但不是端点）上运动时，点Q的轨迹是线段AB的反向延长线；

（3）当点P在线段MB（但不是端点）上运动时，点Q的轨迹是线段AB的延长线；

（4）当点P在线段AB的延长线上运动时，点Q的轨迹是线段MB（但不是端点）.

解题过程略.

注  在射影几何中，把（1）中的定直线叫做定点P关于定曲线C的极线.很多平面解析几何试题都有极点与极线背景［7］［8］.

题7  在平面直角坐标系xOy中，到两个定点F1（-1，0），F2（1，0）的距离的积是定值a2（a>0）的点的轨迹叫做卡西尼（Cassini）卵形线［9］，记作曲线Υa，并把e=1a叫做曲線Υa的离心率，两个定点F1，F2分别叫做曲线Υa的左焦点、右焦点.

（1）求曲线Υa上的点到坐标原点O的距离的取值范围；

（2）对于离心率e>1的曲线Υa：

（i）分别求出该曲线上动点的横坐标、纵坐标的取值范围；

（ii）求证：0

（3）对于离心率e≤22的曲线Υa：

（i）分别求出该曲线上动点的横坐标、纵坐标的取值范围；

（ii）求证：a≥2且该曲线围成图形的面积大于a4-1π.

解答本题时可使用参考结论：长轴长、短轴长分别为u，v的椭圆面积是uvπ.

简解  可先求得动点P的轨迹方程是y2=4x2+a4-x2-1（1-a2≤x2≤1+a2），进而可得答案：

（1）a2-1，a2+1；

（2）（i）1-a2，1+a2，0，a44；（ii）略；

（3）（i）-a2+1，a2+1，-a2-1，a2-1；（ii）略.

注  （1）如图3所示，卡西尼卵形线Υa的形状共包括下面的四种情形［9］：

图3

（i）当0

（ii）当a=1时，Υa成8字形自相交叉，称为“8字形”或双纽线；

（iii）当1

（iv）当a≥2时，Υa是一条没有自交点的光滑曲线但曲线中部凸起（当a越大时，中部凸起的越厉害），稱为“类椭圆”.

（2）若P是曲线Υa上的动点（其两个焦点分别是F1，F2）但不在x轴上，则△F1PF2面积的取值范围是0，12a2.

可得△F1PF2的面积S△F1PF2=12PF1·PF2sin∠F1PF2≤12PF1·PF2=12a2.由图3可知，当点P的纵坐标→0（此种情形存在）时，S△F1PF2→0；当点P是以线段F1F2为直径的圆与曲线Υa的交点（可得两者交点的个数是4）时，S△F1PF2=12a2.因而欲证结论成立.

（3）下面这道高考题的背景就是卡西尼卵形线［9］：

（2011年高考北京卷理科第14题）曲线C是平面内与两个定点F1（-1，0）和F2（1，0）的距离的积等于常数a2（a>1）的点的轨迹，给出下列三个结论：

①曲线C过坐标原点；

②曲线C关于坐标原点对称；

③若点P在曲线C上，则△F1PF2的面积不大于12a2.

其中，所有正确结论的序号是．（答案：②③.）

参考文献

［1］  本刊编辑部.数学科高考最重大最全面的改革［J］.中学数学教学参考（上旬），2024（02）：1.

［2］  甘志国.介绍一道原创“数学文化”高考模拟题［J］.中学数学杂志，2018（03）：48-49.

［3］  甘志国.有趣的方格几何［J］.新高考（高二·数学），2013（11）：39-40.

［4］  甘志国.春节的公历日期［J］.数理天地（高中版），2008（11）：46.

［5］  刘玉琏，傅沛仁.数学分析讲义（上册）［M］.2版.北京：人民教育出版社，1981：258-262.

［6］  魏万迪.整数入门［M］.成都：四川教育出版社，1988.

［7］  甘志国.二次曲线的两条性质及其应用［J］.中学数学杂志，2024（01）：33-38.

［8］  甘志国.对2020年高考数学北京卷第20题与第21题的思考［J］.高中数理化，2020（13-14）：19-21.

［9］  甘志国.高中数学题典：平面解析几何［M］.哈尔滨：哈尔滨工业大学出版社，2016：533.

作者简介  甘志国（1971—），男，湖北竹溪人，研究生学历，正高级教师、特级教师、湖北名师、政府专项津贴专家、北京民进名师专家团专家、甘志国特级教师工作室主持人；2018年7月2日，北京市丰台区教委召开了“北京市特级教师甘志国教育科研研讨会”；对高考数学试题及重点高校强基计划数学试题研究深入；钻研教法与学法，提倡并关注学生运算能力的培养；总结提出并践行“懂、会、熟、巧、通”五步解题学习法，“思、探、练、变、提”五步解题教学法，“知、懂、熟、用、赏”五种解题境界及高中数学教学的四个关键词“夯实基础、激发兴趣、着眼高考、适当提高”；倡导教师要做明师——明白的教师；已发表文章多篇（2016-2023年均发表了北京高考数学试题综述文章），已出版独著61册（总计31 326千字，其中27册署名“甘志国著”）.