极值点偏移问题的探源、拓展及应用

程汉波 黄嵩涛

【摘  要】  “极值点偏移问题”作为导数在研究函数性质中的应用之一，近年来在教研中受到广泛关注．利用泰勒展开这一工具探究后得出：极值点偏移问题是中值点偏移问题的特殊情形，满足罗尔中值定理（或拉格朗日中值定理）条件的至少三阶可导函数中可能会存在“极值点偏移”（或“中值点偏移”）现象，而且，在其三阶导数恒为0时，极值点（或中值点）不偏；在三阶导数不为零且正负性确定的条件下，当二阶导数与三阶导数乘积的为正时，极值点（或中值点）右偏；当二阶导数与三阶导数乘积的为负时，极值点（或中值点）左偏．最后利用探究所得的结果解答三道全国卷中出现的极值点偏移问题，并给出关于高观点对中学数学教学作用的一点感悟．

【关键词】  极值点偏移；泰勒展开；三阶导数；中值点偏移

“极值点偏移问题”作为导数在研究函数性质中的应用之一，近年来在教研中受到广泛关注，在“中国知网”以“极值点偏移”为主题进行搜索可发现，仅标题中含有“极值点偏移”字样的文献就有逾200篇，但细看不难发现，以“例题+解法”居多，如构造对称函数、利用对数平均不等式、比值代换法等处理策略在教研中得到广泛普及且变得愈发成熟．然而，教研文章的数量并不意味着对极值点偏移问题的研究已算圆满．恰恰相反，之所以会有如此多的文章探究这类问题，在一定程度上说明大家对其已有的研究并不完全满意．而且，解法的普及与成熟也说明这类问题具有较强的共性，理应进一步抽象概括出通用解法背后的深层本质．

1  极值点偏移问题简介

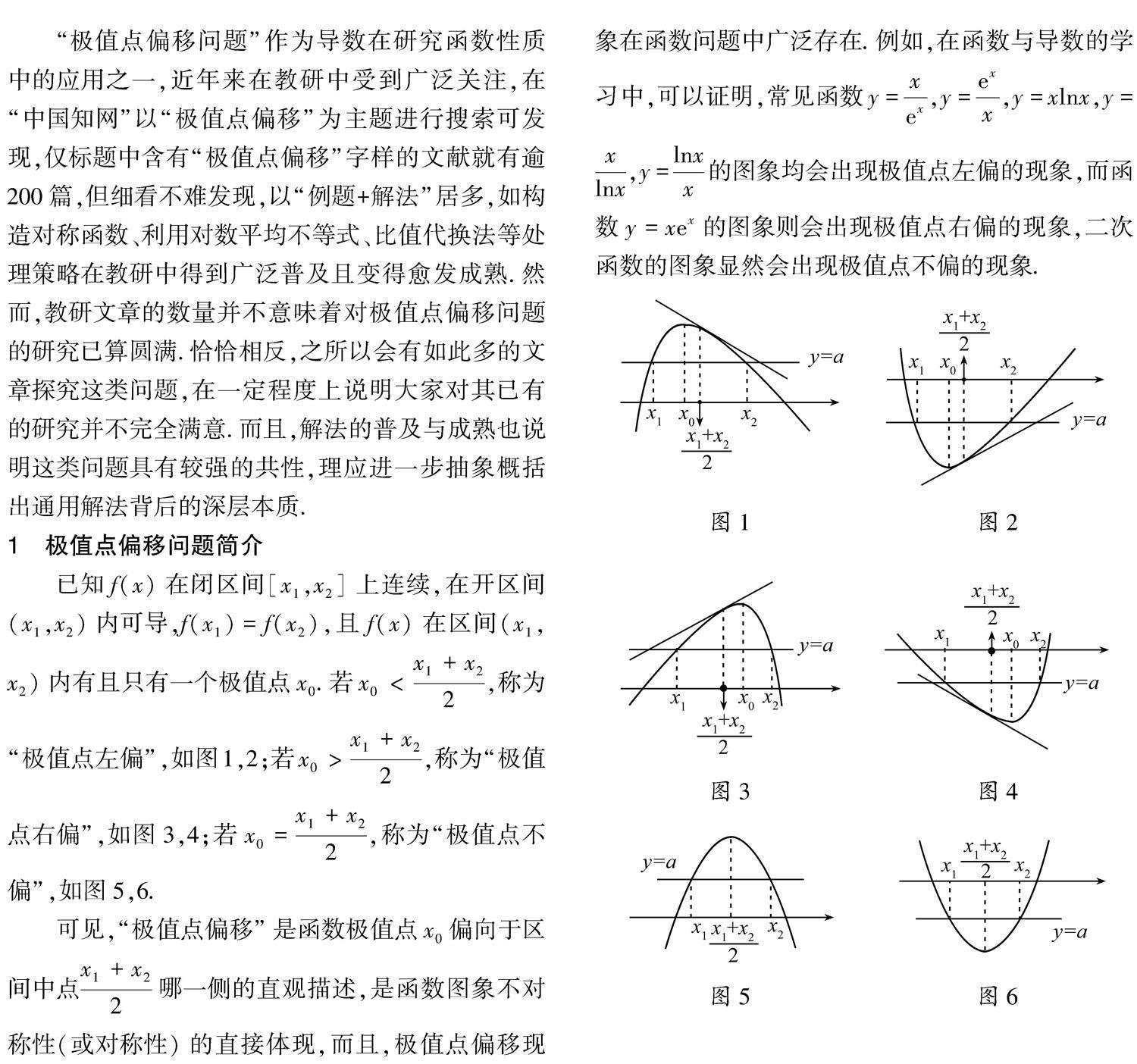
已知f（x）在闭区间［x1，x2］上连续，在开区间（x1，x2）内可导，f（x1）=f（x2），且f（x）在区间（x1，x2）内有且只有一个极值点x0．若x0＜x1+x22，称为“极值点左偏”，如图1，2；若x0＞x1+x22，称为“极值点右偏”，如图3，4；若x0=x1+x22，称为“极值点不偏”，如图5，6．可见，“极值点偏移”是函数极值点x0偏向于区间中点x1+x22哪一侧的直观描述，是函数图象不对称性（或对称性）的直接体现，而且，极值点偏移现象在函数问题中广泛存在．例如，在函数与导数的学习中，可以证明，常见函数y=xex，y=exx，y=xlnx，y=xlnx，y=lnxx的图象均会出现极值点左偏的现象，而函数y=xex的图象则会出现极值点右偏的现象，二次函数的图象显然会出现极值点不偏的现象．

2  极值点偏移问题探源

要比较极值点x0与区间中点x1+x22的大小，注意到f′（x0）=0，故可以先判断出f′x1+x22的正负性，再根据f′（x）的单调性（由f″（x）的正负性决定）得出x1+x22与x0的大小关系．由图1—6可以大致猜测，极值点偏移规律与函数的单调性（一阶导数刻画）及函数的凹凸性（二阶导数刻画）有关，因为函数图象的不对称性（或对称性）本身就与其单调性、凹凸性联系紧密．然而，也不难发现，图1，3，5中函数均为上凸函数，且先增后减，但却出现了不同的极值点偏移现象；同样地，图2，4，6中函数均为下凸函数，且先减后增，也出现了不同的极值点偏移现象．这表明直接由图1—6归纳出极值点偏移规律稍显困难，还需更精细化的考察，下面用泰勒展开这一高等数学工具探究f′x1+x22的正负性的判定条件，并进一步得到极值点偏移规律更本源的刻画方式，具体过程与结果如下．

假定f（x）至少三阶可导，记m=x1+x22，将f（x1）与f（x2）分别在x=m处泰勒展开得，

f（x1）=f（m）+f′（m）（x1-m）+f″（m）2（x1-m）2+f（ξ1）6（x1-m）3（x1＜ξ1＜m）;

f（x2）=f（m）+f′（m）（x2-m）+f″（m）2（x2-m）2+f（ξ2）6（x2-m）3（m＜ξ2＜x2）．

因为f（x1）=f（x2），将以上两式相减可解得，

f′（m）=-f（ξ1）+f（ξ2）48·（x1-x2）2.（*）

（1）当f（x）=0时，由于f（x）在区间（x1，x2）内只有一个极值点x0，因此f″（x）为非零常数，则f′（x）为单调函数．由（*）式知，f′（m）=0=f′（x0），所以m=x1+x22=x0．

（2）当f（x）＞0时，由（*）式知，f′（m）＜0=f′（x0），则

①当f″（x）＞0时，f′（x）单调递增，则m=x1+x22＜x0；

②当f″（x）＜0时，f′（x）单调递减，则m=x1+x22＞x0．

（3）当f（x）＜0时，由（*）式知，f′（m）＞0=f′（x0），则

①当f″（x）＞0时，f′（x）单调递增，则m=x1+x22＞x0；

②当f″（x）＜0时，f′（x）单调递减，则m=x1+x22＜x0．

综上所述，当f（x）=0时，x1+x22=x0；当f（x）·f″（x）＞0時，x1+x22＜x0；当f（x）·f″（x）＜0时，x1+x22＞x0．

值得一提的是，以上综述结果中f（x）·f″（x）＞0是指f″（x）＞0，f（x）＞0或f″（x）＜0，f（x）＜0两种情形，并不包括f″（x）或f″（x）的正负性不完全确定的情形；类似地，f（x）·f″（x）＜0是指f″（x）＞0，f（x）＜0或f″（x）＜0，f（x）＞0两种情形．下文与之类似，不再赘述．

因此，至少三阶连续可导函数的极值点偏移问题可用其二阶导数与三阶导数共同刻画．具体地，三阶导数是否为0可断定极值点是否会发生偏移，在三阶导数不为零且正负性确定的条件下，二阶导数与三阶导数乘积的正负性可断定是极值点左偏还是极值点右偏．例如，二次函数的三阶导数恰好等于0，会出现“极值点不偏”的现象，这与其图象是轴对称图形的直观相一致；函数y=xlnx的二阶、三阶导数分别为y″=1x＞0， y=-1x2＜0，则

y″y=-1x3＜0，这与其图象在区间0，1上会出现“极值点左偏”（即x0=1e＜x1+x22）的现象相一致；函数f（x）=xex的二阶、三阶导数分别为f″（x）=（x+2）ex，f（x）=

（x+3）ex，则f″（x）·f（x）=（x+2）（x+3）e2x，由f（x1）=f（x2）可推得x1，x2＜0，当x1，x2中有变量小于等于-2时，“极值点右偏”（即x0=-1＞x1+x22）显然成立；当-2＜x1，x2＜0时，有f″（x）＞0， f（x）＞0，则f″（x）f（x）＞0，“极值点右偏”也成立．因此，这三个特例恰好印证了前面所得的结论．

3  极值点偏移问题拓展

由极值点偏移问题的条件和结论不难联想起罗尔中值定理：若闭区间［x1，x2］上的连续函数f（x）在开区间（x1，x2）内可导，且f（x1）=f（x2），则在（x1，x2）内至少存在一点ξ（称其为中值点），使得f′（ξ）=0．上文讨论结果表明，在中值点唯一的前提下，有时可以根据f（x）的二阶导数f″（x）与三阶导数f（x）的正负性，得到中值点ξ与区间中点x1+x22的大小关系．因此，极值点偏移问题也可以看作中值点偏移问题的特殊情形，都是比较极值点（或中值点）ξ与区间中点x1+x22的大小关系，进而得出极值点（或中值点）ξ相对于区间中点x1+x22的偏移方向，它是对罗尔中值定理中存在性结果的进一步深入细致的探究．

于是，不禁又联想起拉格朗日中值定理：若闭区间［x1，x2］上的连续函数f（x）在开区间（x1，x2）内可导，则在（x1，x2）内至少存在一点ξ，使得f′（ξ）=f（x2）-f（x1）x2-x1．在中值点ξ唯一的条件下，能否类似地探究中值点ξ与区间中点x1+x22的大小关系呢？不难发现，该问题是极值点偏移问题的拓展推广，它的解决可以进一步的揭示极值点偏移问题的本质．经历一番探究，得到以下结果：

定理  若闭区间［x1，x2］上的连续函数f（x）在（x1，x2）内至少三阶可导，且f′（x）不为常数，则

（1）若f（x）=0，则存在唯一ξ=x1+x22，使得f′（ξ）=f（x2）-f（x1）x2-x1；

（2）若f（x）·f″（x）＞0，则存在唯一ξ∈x1+x22，x2，使得f′（ξ）=f（x2）-f（x1）x2-x1；

（3）若f（x）·f″（x）＜0，则存在唯一ξ∈x1，x1+x22，使得f′（ξ）=f（x2）-f（x1）x2-x1．

证明  记x1+x22=m，将f（x1）与f（x2）分别在x=m处泰勒展开得，

f（x1）=f（m）+f′（m）（x1-m）+f″（m）2（x1-m）2+f（ξ1）6（x1-m）3（x1＜ξ1＜m）;

f（x2）=f（m）+f′（m）（x2-m）+f″（m）2（x2-m）2+f（ξ2）6（x2-m）3（m＜ξ2＜x2）．

将以上两式相减可得，

f（x1）-f（x2）=f′x1+x22（x1-x2）+f（ξ1）+f（ξ2）48（x1-x2）3．

在区间［x1，x2］上由拉格朗日中值定理知，存在ξ∈（x1，x2），使得

f′（ξ）=f（x1）-f（x2）x1-x2=f′x1+x22+f（ξ1）+f（ξ2）48（x1-x2）2.（**）

（1）当f（x）=0时，结合f′（x）不为常数，则f″（x）为非零常数，因此f′（x）为单调函数．由（**）式知，f′（ξ）=f′x1+x22，所以存在唯一ξ=x1+x22．

（2）当f（x）·f″（x）＞0时，则可分两种情况：

①当f（x）＞0， f″（x）＞0時，由（**）知，f′（ξ）＞f′x1+x22，且f′（x）单调递增，所以存在唯一ξ∈x1+x22，x2；

②当f（x）＜0， f″（x）＜0时，由（**）知，f′（x0）＜f′x1+x22，且f′（x）单调递减，所以也存在唯一ξ∈x1+x22，x2．

（3）与（2）类似可证，此处略去．

由此可知，极值点偏移问题确实就是中值点偏移问题的特殊情形，任何满足拉格朗日中值定理条件的函数中均可能会存在中值点偏移现象．具体地，对于满足拉格朗日中值定理条件且至少三阶可导的函数，其三阶导数是否为0可断定中值点是否会发生偏移，在三阶导数不为零且正负性确定的条件下，二阶导数与三阶导数乘积的正负性可断定中值点是左偏还是右偏．例如，对于对数函数f（x）=lnx，其二阶、三阶导数分别为f″（x）=-1x2＜0， f（x）=2x3＞0，则f″（x）·f（x）＜0，因此会出现“中值点左偏”的现象，即存在唯一ξ∈x1，x1+x22，使得f′（ξ）=f（x2）-f（x1）x2-x1=lnx2-lnx1x2-x1．又因为f′（x）=1x单调递减，所以f′（ξ）＞f′x1+x22，即lnx2-lnx1x2-x1＞2x1+x2，该不等式即为“对数平均不等式”的一部分，它在解决与自然对数有关的“极值点偏移问题”屡建奇功，在教学、教研中已发展为一种重要的策略工具．由此观之，“对数平均不等式”之所以会如此有效，部分原因是因为该结果就是对数函数中“中值点偏移问题”的代数刻画，当然可在“极值点（即中值点）偏移问题”中大放异彩．类似地，对指数函数f（x）=ex，不难由“中值点偏移问题”的结果得ex1-ex2x1-x2＞ex1+x22，也有人将其称为“指数平均不等式”，它在解决指数函数有关的“极值点（即中值点）偏移问题”时也照样大放异彩．

4  高考中的极值点偏移问题

近些年来，极值点偏移问题的例子众多，笔者在教学实践中发现，大都可用以上结论解决，既简明快捷又贴近本質．本文仅给出全国高考卷中对极值点偏移问题的研究热点“推波助澜”的三道高考题及解答，更多的例子读者在实践中可不断尝试．

例1  （2016年全国高考新课标Ⅰ卷（乙卷）第21题）已知函数f（x）=（x-2）ex+a（x-1）2有两个零点．

（Ⅰ）求a的取值范围；

（Ⅱ）设x1，x2是f（x）的两个零点，证明：x1+x2＜2．

证明   （Ⅰ）a＞0，过程略；（Ⅱ）由（Ⅰ）知，a＞0，且x1＜1＜x2＜2，则

①当x1＜0时，由x2＜2得，x1+x2＜2；

②当x1≥0时，f′（x）=（x-1）ex+2a， f″（x）=xex+2a， f（x）=x+1ex，则当x∈［x1，x2］时，有f″（x）＞0， f（x）＞0，则f″（x）·f（x）＞0，所以x1+x22＜1，即x1+x2＜2．

例2  （2021年全国新高考Ⅰ卷第22题）已知函数f（x）=x（1-lnx）.

（Ⅰ）讨论f（x）的单调性；

（Ⅱ）设a，b为两个不相等的正数，且blna-alnb=a-b，证明：1a+1b＞2．

证明  （Ⅰ）略；（Ⅱ）由（Ⅰ）知，f（x）在（0，1）上单调递增，在（1，+∞）上单调递减．注意到blna-alnb=a-b即为f1a=f1b，不妨设1a=x1∈（0，1），1b=x2∈（1，+∞），则原问题等价于证明x1+x2＞2．

①当x2≥2时，由x1＞0得，x1+x2＞2；

②当x2＜2时，f′（x）=-lnx， f″（x）=-1x， f（x）=1x2，则当x∈［x1，x2］时，有f″（x）＜0， f（x）＞0，则f″（x）·f（x）＜0，所以x1+x22＞1，即x1+x2＞2．

例3  （2022年全国高考甲卷第21题）已知函数f（x）=exx-lnx+x-a.

（Ⅰ）f（x）≥0，求a的取值范围；

（Ⅱ）若f（x）存在两个零点x1，x2，证明：x1x2＜1．

证明  （Ⅰ）略；（Ⅱ）由f（x1）=f（x2）得，ex1x1-lnx1+x1-a=ex2x2-lnx2+x2-a，即ex1x1+lnex1x1=ex2x2+lnex2x2．记g（x）=x+lnx，则gex1x1=gex2x2．易知g（x）单调递增，则ex1x1=ex2x2，两边取自然对数得，x1-lnx1=x2-lnx2．注意到x1，x2＞0，要证明x1x2＜1，只需证明lnx1+lnx2＜0，又记h（x）=ex-x，则hlnx1=hlnx2，且h′（x）=ex-1，h″（x）=h（x）=ex＞0，则h″（x）·h（x）＞0，所以lnx1+lnx22＜0，即x1x2＜1．

5  余话与启示

众所周知，微积分的诞生与运动学息息相关．例如，位移对时间的一阶导数是速度，用以描述运动的快慢；位移对时间的二阶导数是加速度，用以描述速度变化的快慢．不禁产生疑问：位移对时间的三阶导数及其物理意义是什么呢？由文［3］［4］可知，牛顿力学框架体系对加速度的变化并未给出任何实质性的描述，但随着汽车、火车、公路、铁路等人类物质文明的发展，到19世纪中叶，人们认识到加速度的变化快慢会引起舒适感的不同，这与机械元件（如凸轮、轨道）的设计有关，于是将位移对时间的三阶导数称为急动度，用以描述加速度的变化快慢．

同样地，微积分的诞生与几何学也息息相关．例如，函数的一阶导数的几何意义为切线斜率，用以描述函数的单调性；函数的二阶导数可以表示切线斜率的变化快慢，用以描述函数的凹凸性．不禁产生疑问：函数的三阶导数及其几何意义是什么呢？它描述了函数哪方面的性质呢？本文探究得出，极值点偏移问题是中值点偏移问题的特殊情形，对于满足拉格朗日中值定理（或罗尔中值定理）条件且至少三阶可导的函数，其三阶导数是否为0可断定中值点是否会发生偏移，在三阶导数不为零且正负性确定的条件下，二阶导数与三阶导数乘积的正负性可断定是中值点左偏还是中值点右偏．

用泰勒展开式的观点来看极值点（或中值点）偏移问题，它不仅提供了解决问题的一种策略，也是命制相关试题的一条渠道．更深入地揭示这类问题的本质．这启示我们中学教师应主动探寻初等数学与高等数学知识的结合点，从而对中学数学知识有一个更深层次的理解．教师只有站在较高的角度审视数学问题，才能将问题看得更清楚，更透彻．这正如F·克莱因所认为的，“教师掌握的知识要比他所教的多得多，才能引导学生绕过悬岩，渡过险滩”．

德国哥廷根数学学派领袖菲利克斯·克莱因曾说：“数学教师应站在更高（高等数学）视角审视、理解初等数学问题，只有观点高了，事物才能显得明了而简单；有许多初等数学的现象只有在非初等的理论结构内才能深刻地理解．”杜甫诗云：“会当凌绝顶，一览众山小”.就事论事地看待中学数学，只是知其然，用高等数学的数学方法进行解读，就会豁然开朗，不仅知其然，更知其所以然．我国有一句著名教育格言“要给学生一杯水，教师应该有一桶水”，说的也是这层意思．

参考文献

［1］  甘大旺．函数极值点偏移问题新论［J］．数学通讯：下半月，2017（07）：44-47．

［2］  朱华伟，程汉波，杨春波．2016年全国卷Ⅰ压轴题的解法赏析、探究与思考［J］．数学通讯：下半月，2017（11）：26-30．

［3］  黄沛天.一个描写机械运动的新概念：急动度［J］.物理，1981（07）：394-397.

［4］  黄沛天，黄文，胡利云.变加速运动理论与实践意义初探［J］.江西师范大学学报（自然科学版），2003（01）：8-11.

［5］  陈月兰．高观点下的初等数学［M］．上海：上海华东师范大学出版社，2011．

作者简介

程汉波（1990—），男，湖北孝感人，博士，高中数学一级教师，主要从事数学教育研究．

黄嵩涛（1989—），男，湖北武汉人，博士研究生，高中数学一级教师，主要从事数学教育研究．