基于迭代式粒子群优化的永磁同步电机热网络模型参数辨识研究

摘 要：

针对集总参数热网络模型未知参数多、参数辨识收敛困难的问题，利用永磁同步电机在不同工况下的特性，提出迭代式粒子群优化辨识框架，用实验测量的电机温度场数据，以各节点估计温度与实测温度的均方误差作为目标函数，将并行优化转化为三步串行迭代优化，减少每一步优化变量数，缩小种群规模，避免陷入局部最优。应用于某额定功率70 kW电机，得到一般热阻和热容随温度变化的规律，电机损耗、绕组涡流系数和气隙热阻随转速变化的规律。台架实验表明，在综合驾驶工况下，以槽内绕组、端部绕组、永磁体、定子齿和定子轭的温度估计最大误差和平均误差作为评价指标，与实测结果以及传统的采用固定参数的集总参数模型相比，提出的模型精确度高，工况适应性好。

关键词：永磁同步电机；集总参数热网络；温度实时估计；温度依赖性；参数辨识；迭代式粒子群优化

DOI：10.15938/j.emc.2024.01.001

中图分类号：TM341

文献标志码：A

文章编号：1007-449X（2024）01-0001-11

Iterative particle swarm optimization based parameter identification of lumpedparameter thermal network for permanent magnet synchronous motors

MENG Zhijin，"LIU Yuyang，"CHEN Li

（Key Laboratory of Marine Intelligent Equipment and System of Ministry of Education， Shanghai Jiao Tong University， Shanghai 200240， China）

Abstract：

Addressing the problem of nonconvergent parameter identification due to many unknown parameters， a frame of iterative particle swarm optimization was proposed to identify the parameters in three iterative steps. Using experimentally measured motor temperature field data， with the mean square error between the estimated and measured temperatures at each node as the objective function， parallel optimization was transformed into a threestep serial iterative optimization. The number of optimization variables were reduced at each step， the population size was shrunk， and falling into local optima was avoided. The frame was applied to a fivenode lumpedparameter thermal network （LPTN） model of a motor with rated power at 70 kW. The identified parameters demonstrate the change of the ordinary thermal resistance and capacities with temperature， the change of the motor losses， the eddycurrent coefficient of stator resistance and air gap thermal resistance with the motor speed. The identification performance is evaluated in terms of the maximum error and average error of temperature at the activewinding， endwinding， permanent magnet， stator tooth and stator yoke. Dynamometer experiments conducted under comprehensive operating conditions validate that， compared with experimental measurements and traditional lumped parameter models that adopt fixed parameter values， the proposed model gains higher accuracy and better adaptability to different operating conditions compared with the conventional LPTN model with fixed parameters.

Keywords：permanent magnet synchronous motor; lumpedparameter thermal network; online temperature prediction; temperature dependence; parameter identification; iterative particle swarm optimization

0 引 言

永磁同步电机功率密度高，转矩、转速范围宽，在电动汽车、船舶等领域得到广泛应用[1]。近年来，随着功率密度的提高，热负荷引起电机温升受到关注，绕组过热导致绝缘层损伤，永磁体温度过高发生不可逆退磁，从而降低电机性能，缩短使用寿命[2-3]。由于绕组绕制紧密以及转子旋转运动，内部不便于安装热电偶。因此，建立在线温度模型，实时、准确估计电机温度，对电机安全高效运行具有重要意义。

电机温度随时间和空间位置而变化，通常采用有限元传热模型[4]和计算流体力学热流耦合模型[5]进行温度估计，精确度较高，但计算负荷大，耗时长，无法实时应用[6-7]。将数据驱动的机器学习模型应用于电机温度估计，可提高计算效率，但是模型训练需要大量数据，且估计精确度和工况适应性受限于训练数据的覆盖度[8-9]。集总参数热网络模型（lumped"parameter thermal network，LPTN）假设节点容积温度场均匀分布，降低温度场计算量，当节点分布合理、参数准确时，可获得较高的估计精确度，在电机温度估计中，具有兼顾精确度与效率的优势[10-11]。实验表明，永磁同步电机槽内绕组、端部绕组、定子轭、定子齿以及转子等部位之间温差较大，但是这些部位内部温差较小，可适用温度均布假设[12]。比如，具有散热翅片的永磁同步电机LPTN模型，13个节点，56个热阻、13个热容、10种损耗，通过参数调校，端部绕组、定子轭和永磁体的最大估计误差分别可达4、43和07 ℃[13]。某交搓齿永磁直线电机的三维LPTN模型，34个节点，72个热阻、34个热容、6种损耗，估计精确度与有限元热模型相当，而计算时间从15 min缩短至5 s[14]。但是，LPTN模型精确度取决于热阻、热容、损耗系数等参数取值准确性。受到节点容积区域几何特征、物理属性以及电机工作频率、磁链、温度的复杂影响，参数调校非常困难。

LPTN模型建立每个节点的能量平衡方程，节点具有热容属性，相邻节点间通过热阻传递热量，节点内热源来自电机损耗，因此，节点方程组维数小于热阻、热容、损耗系数等未知参数个数，参数辨识存在多解，导致辨识算法难以收敛。采用经验公式估算参数值，算法简单，但是准确性低。比如，文献[15]根据材料物性和几何信息估算热阻，设置损耗系数为常数，未考虑热容，因此该LPTN模型仅适用于稳态温度场。文献[16]中，热阻和热容按照经验公式估算，损耗由有限元模型离线计算给出。引入辨识算法，以降低LPTN模型中各节点温度估计误差为优化目标，构建多目标、多变量优化问题，迭代更新参数值。由于计算量大，收敛困难，一般仅辨识部分参数。文献[17]采用扩展卡尔曼滤波算法更新热阻值，然而，热容未更新，且损耗项未计入铁损。文献[18]采用遗传算法辨识绕组导热系数、等效气隙厚度、机壳表面对流换热系数。考虑热阻、热容和损耗等共计30个参数，文献[19]将粒子群优化与序列二次规划相结合并行辨识，针对多解和局部最优问题，采用独立交叉验证方法进行收敛判断。多解问题求解的收敛性，仍然是永磁同步电机LPTN模型参数辨识的难点。

粒子群优化是一种基于群集智能的并行算法，利用种群中个体对信息的共享，使种群的运动在求解空间中产生从无序到有序的演化，从而获得最优解，算法稳定性和收敛性得到证明[20]。进一步，通过加速收敛提高寻优效率，粒子群优化的收敛性在多变量、多目标优化问题中具有显著优势[21]。文献[22]采用动态聚类，在每次迭代后将种群动态地划分为优质群和劣质群，分别以不同速度更新。文献[23]采用岛屿模型将种群划分成多个亚种，通过亚种并行计算加速收敛。文献[24]通过引入共享学习因子对速度更新公式进行改进。

与上述方法不同，本文利用永磁同步电机不同工况下的特性，提出迭代式粒子群优化（iterative particle swarm optimization，IPSO）方法，将并行优化转化为三步串行迭代优化，减少每一步的优化变量数，从而缩小种群规模，提高收敛性。针对5节点LPTN模型中热阻、热容、损耗系数17个参数，第一步，考虑电机停转、冷却工况下损耗为0，利用该工况实验数据辨识一般热阻、热容，优化变量减少至10个，辨识结果传递给后续步骤；第二步，利用基转速以下工况的实验数据，避免高转速对气隙热阻、涡流系数产生影响，辨识定子铁损、转子损耗，优化变量减少至2个；第三步，考虑转速的影响，利用全转速范围实验数据，辨识气隙热阻和涡流系数，优化变量也减少至2个。从第一步到第三步循环迭代，直到LPTN模型精确度满足要求。这样即可适当减少优化求解的计算量，又可发挥粒子群优化收敛性强的优势，避免陷入局部最优。

本文将IPSO应用于额定功率70 kW的车用水冷内置式永磁同步电机，辨识得到5节点LPTN模型中热阻、热容随温度变化的规律，电机损耗、涡流系数、气隙热阻随转速变化的规律。基于这些规律进行插值得到参数值，完善LPTN模型，通过实验验证LPTN模型精确度和工况适应性。

1 电机LPTN模型

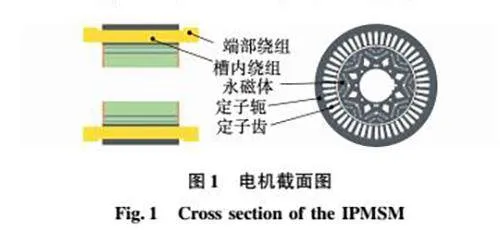
本文研究的水冷内置式永磁同步电机截面如图1所示。考虑槽内绕组、端部绕组、定子轭、定子齿、转子永磁体这5个部位之间温度差别较明显[12]，设计5节点LPTN模型，如图2所示。研究对象为水冷电机，热量主要由冷却水带出，机壳对散热的影响较小。实验表明，如图3所示，电机在转速4 600 r/min、转矩180 N·m工况持续运行600 s和1 200 s时，机壳温度平均温度均为343 ℃，与环境温度相当。因此，机壳不必单独设置节点。

LPTN模型中，C表示节点热容，P表示节点容积的损耗功率，R表示节点之间的热阻，下标中，aw、ew、sy、st和pm分别表示槽内绕组、端部绕组、定子轭、定子齿、永磁体节点。TC为冷却水平均温度，按进、出口温度测量值的算术平均，TA为环境温度，由热电偶直接测得。

电机定子、转子均产生损耗，其中定子损耗包括定子铜损和定子铁损，转子损耗包括永磁体损耗、转子铁损和机械损耗。下面分别给出计算模型。

1.1 定子铜损

1.2 定子铁损

式中：kh、kc、ke分别为基于磁链计算铁耗的磁滞损耗系数、涡流损耗系数和异常损耗系数，本文将在不同的转速和负载工况下对其进行辨识；ψ为气隙磁链幅值。

定子铁损PFe分布于定子轭和定子齿，定义定子轭上的铁损分配系数ε，则定子轭节点损耗

本文通过实验测量得到d-q坐标系下的电压ud、uq，电流id、iq和电机电角速度等信息，将不同工况下的定子铁心损耗作为输出，将对应工况的基波电流频率和离线辨识得到的永磁体磁链作为输入，经过多元非线性拟合方法得到铁心损耗系数，kh、 kc和ke。

1.3 转子损耗

如图2所示，本文将转子整体看作一个节点，转子损耗按下式计算[28-29]：

2 基于IPSO的参数辨识

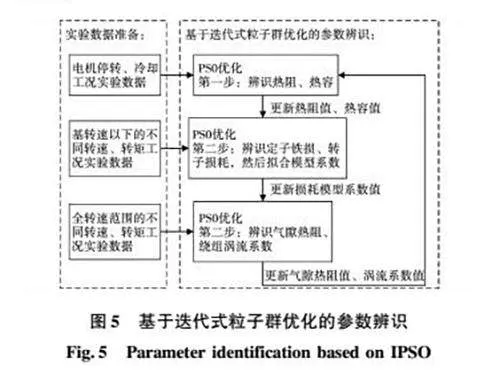
基于IPSO对电机LPTN模型进行参数辨识的流程如图5所示。未知参数按照与损耗、转速的相关性分为三类，第一类为一般热阻与热容，即式（1）中的矩阵A和矩阵C；第二类为损耗系数kh、 kc、ke；第三类为涡流系数kR和气隙热阻Rpm，st。相应地，IPSO分为三步，每一步准备相应的实验数据，用于判定辨识结果的合理性。第一步利用电机停转、冷却工况实验数据，辨识一般热容、热阻。第二步，利用基转速之下不同转速、转矩工况的实验数据，辨识定子铁损、转子损耗，并进一步拟合得到式（6）、式（10）中的系数，也避免了高转速对气隙热阻Rpm，st、涡流系数kR产生影响。第三步，利用全转速范围的实验数据，辨识kR，并修正Rpm，st。从第一步到第三步循环迭代，直到LPTN模型精确度满足要求。

2.1 实验数据的获取

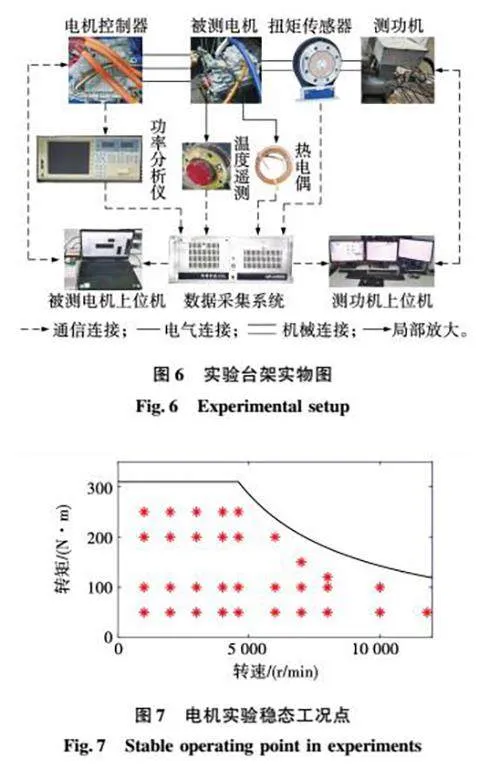
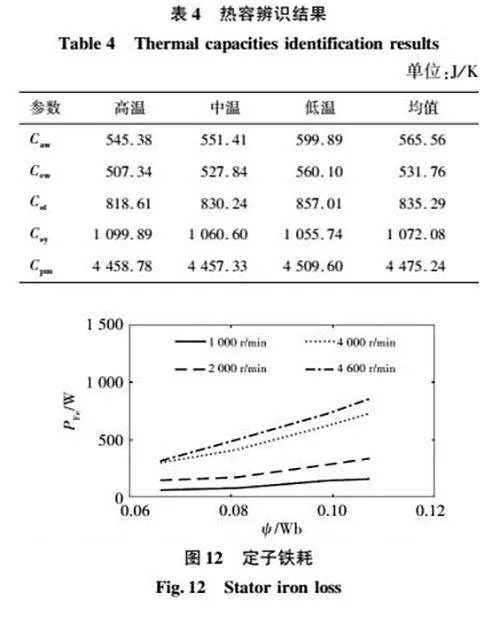
实验台架如图6所示，测功机与被试电机之间安装扭矩传感器，电机定子齿部、轭部、槽内绕组、端部绕组和转子部位安装K型热电偶。转子温度由德国MANNER公司的温度遥测装置进行信号采集、放大、射频传输和天线接收。遥测装置通道数为8，采样率100 Hz，最大允许转速20 000 r/min。d、q轴电流由电机控制器提供。数据采集设备为NI公司PXI机箱和板卡PXIe-4353。此外，电机冷却水温度由水冷机进行调节，设定温度25 ℃，冷却水流量12 L/min。实验中，测功机上位机发送转速指令，被试电机控制器发送转矩指令，被测电机按照预设稳态工况点或动态测试循环运行。稳态工况点如图7所示。

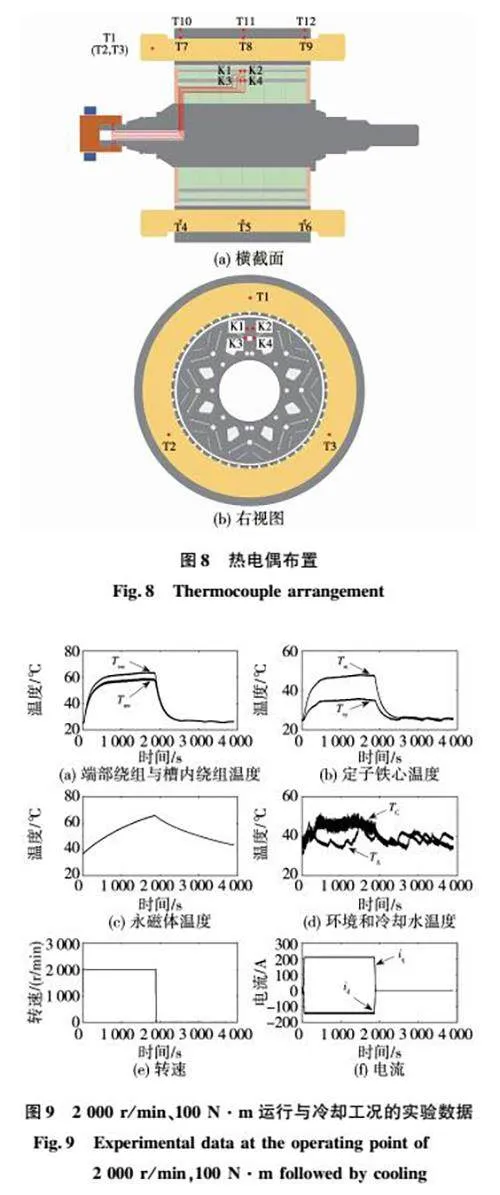
热电偶布置如图8所示，T1～T3沿周向均匀安装在端部绕组上，取T1～T3热电偶的平均值作为端部绕组温度Tew；T4～T6、T7～T9以及T10～T12分别沿轴向均匀安装在槽内绕组、定子齿和定子轭，分别取平均值作为槽内绕组温度Taw、定子齿温度Tst以及定子轭温度Tsy。K1～K4安装在双V型永磁体附近，取平均值作为永磁体温度Tpm。

以稳态工况点（转速2 000 r/min、转矩100 N·m）运行2 000 s、然后冷却的过程为例，实验中采集数据如图9所示，用于LPTN参数辨识与验证。

2.2 IPSO算法

粒子群优化算法由种群中不同粒子之间的相互配合实现对搜索空间的寻优。种群中每个个体包含该个体的当前位置、当前移动速度以及历史个体最佳位置等信息。在个体迭代更新时，其新的位置受个体和群体的综合影响，个体下一时刻速度由当前速度、个体历史最优位置、全局最优位置共同决定；个体下一时刻位置由当前位置和更新之后的速度决定。通过比较个体位置更新后的适应度与个体历史最优适应度以及全局最优适应度，实现个体最优和全局最优的更新。随着迭代的继续，实现对最优解的搜索[30]。

按定子和转子将热阻、热容参数分为两组，并将IPSO第一步分解为两个子步骤，每个子步骤按照辨识对象分别建立优化目标函数。当辨识定子热阻、热容时，以定子各节点估计的温度与实验测量值的均方差最小作为目标函数，即

其中epm表示永磁体节点温度的估计误差。

考虑IPSO的第二步和第三步均为从全局角度出发，意图提高所有节点的辨识精确度，因此，这两步均以所有节点的估计温度与实验测量值的均方差最小作为目标函数，表示为

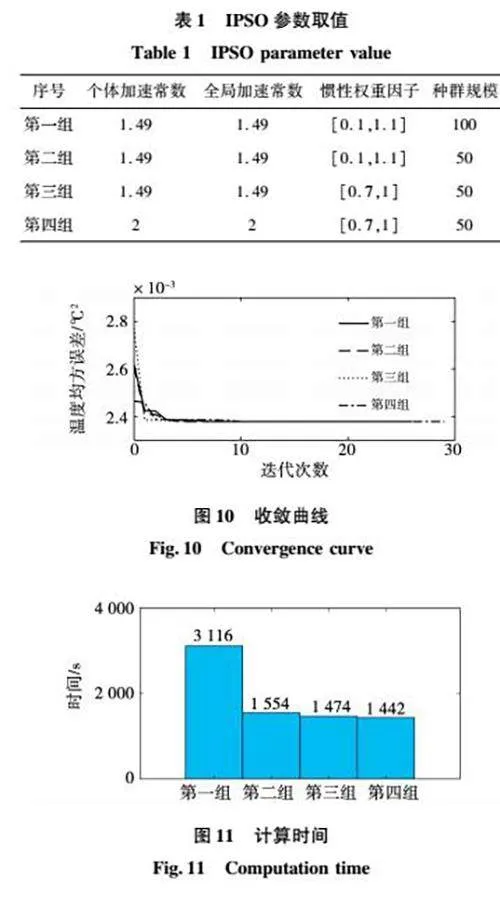
本文调用MATLAB中的函数particleswarm（）进行离线识别。为了调试参数获得合理取值，本文基于常规经验选择4组参数值[31-33]，如表1所示。考虑优化耗时较长，将参数值应用于IPSO第一步中转子参数的辨识，收敛曲线和计算时间的比较分别如图10、图11所示。可见，迭代次数超过30，温度均方误差已达收敛。为了避免算法提前停止，设置最大迭代次数的上限为300，满足收敛要求。种群规模增大明显延长计算时间，综合考虑收敛性和计算时间，本文选择第四组参数值进行优化。此外，由于IPSO第一步中定子的待辨识参数较多，收敛较困难，将其种群规模扩到为100。

3 参数辨识结果

本节给出IPSO的参数辨识结果，按照3步迭代框架，分别给出一般热阻与热容随温度的变化规律、定子铁耗和转子损耗随工况的变化规律、气隙热阻与绕组涡流系数随转速的变化规律。

3.1 一般热阻与热容

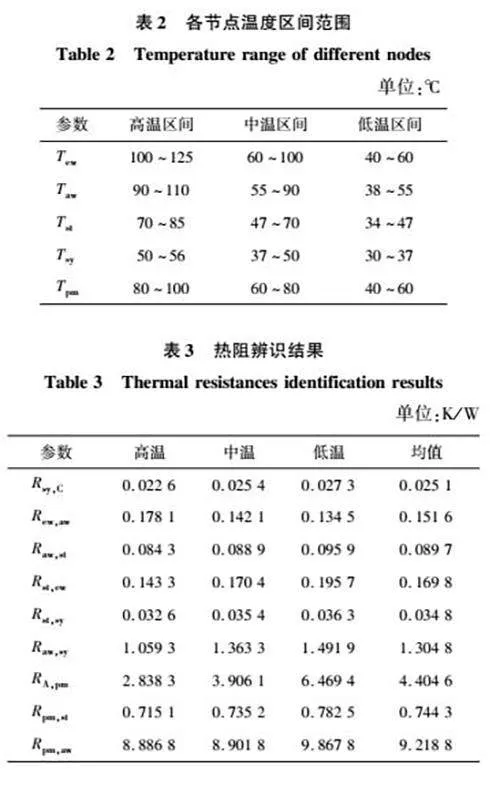
根据定子齿部、定子轭部、端部绕组和槽内绕组、永磁体温度的实测值，将电机温度划分为3个区间，如表2所示。在各区间内，分别利用相应的实验数据进行参数辨识。

3个温度区间中，LPTN模型中9个热阻的辨识结果如表3所示。这些热阻主要由两种介质材料组成，即硅钢和空气。文献研究表明，硅钢材料的导热系数随温度升高而降低，即热阻随温度升高而增大[34]；空气的导热系数随温度升高而增加，即热阻随温度升高而减小[35]。主要由于这两种介质的综合作用，9个热阻随温度表现出不同的变化规律。热阻Rsy，C、Rst，ew、RA，pm、Rpm，st、Raw，st、Rst，sy、Raw，sy和Rpm，aw中，空气热阻作用较强，热阻随温度升高而减小，变化幅度分别为2080%、3657%、12793%、943%、1376%、1135%、4084%和1104%。热阻Rew，aw中，硅钢片作用较强，热阻随温度升高而增大，变化幅度为3242%。考虑热阻随温度的变化剧烈程度，基于辨识结果，插值得到对应温度区间内的热阻，便于LPTN模型取值。

LPTN模型5个热容的辨识结果如表4所示。总体上，在不同温度区间中，热容值有所变化，但变化量不大。其中：Csy、Cpm随温度升高有所增大，符合一般金属热容随温度升高而升高的规律[36]。Caw、Cew和Cst随温度升高有所减小，与均值偏差小于25%，该偏差应主要来自辨识误差。因此，在LPTN模型中，取平均值为热容值。

3.2 定子铁耗PFe与转子损耗Ppm

不同电机转速工况下定子铁耗PFe随着电机磁链ψ变化的辨识结果如图12所示。可见，转速越高，定子铁耗越大；定子磁链越大，定子铁耗越大。而且，转速越高，定子铁耗随着定子磁链的增长率也越大。采用图12的数据，按照式（6），进一步辨识得到kh=81347、kc=192、ke=049。

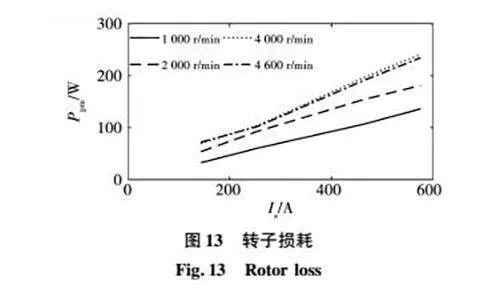
不同电机转速工况下的转子损耗Ppm随着电流幅值Is变化的辨识结果如图13所示。可见，转速越高，转子损耗越大；电流幅值越大，转子损耗越大。采用图13的数据，按照式（10），进一步辨识得到a=0398、b=0784。

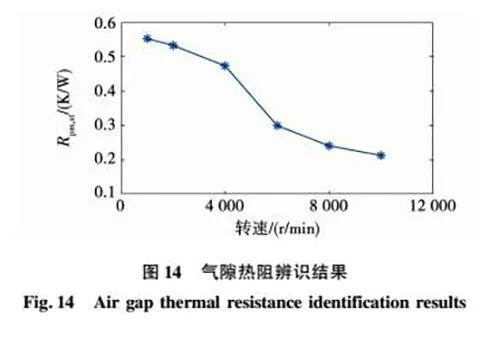
3.3 气隙热阻Rpm，st与绕组涡流系数kR

气隙热阻Rpm，st的辨识结果如图14所示，随电机转速增大而减小，当转速为1 000 r/min时，Rpm，st为0552 3 K/W，当转速为10 000 r/min时，Rpm，st为0213 6 K/W，后者仅为前者的387%。与表3中的Rpm，st值相比较，可见，转速的影响远超过温度的影响。其原因为转速增大时，气隙中的空气与定子、转子表面之间的相对转速增大，从而对流换热能力增强，使得热阻减小。基于该规律，LPTN模型中采用气隙热阻Rpm，st相对于转速的拟合多项式。

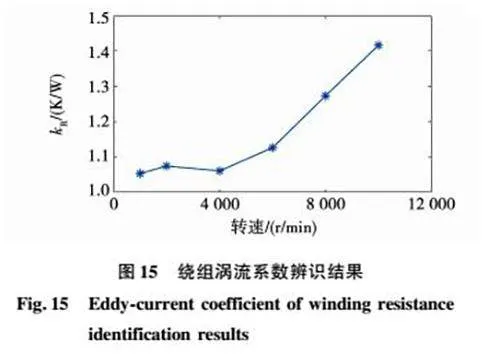
绕组涡流系数kR的辨识结果如图15所示，随着转速增大而增大，当转速为1 000 r/min时，kR为1054 2，当转速为10 000 r/min时，kR为1415 5，后者为前者的134倍。其原因是电机转速增大时，涡流效应增强，使得绕组阻值增大。基于该规律，LPTN模型中采用kR相对于转速的拟合多项式。

4 LPTN模型工况适应性验证

采用本文辨识得到的参数值，更新被测电机的LPTN模型，温度结果表示为“IPSO"LPTN”，与台架实验结果相比较，以验证基于参数辨识的LPTN模型的工况适应性。作为比较，也给出传统的采用固定参数取值的LPTN模型的温度估计结果，表示为“C"LPTN”，其热阻、热容等参数值通过粒子群算法并行辨识优化得到，未区分温度、转速。

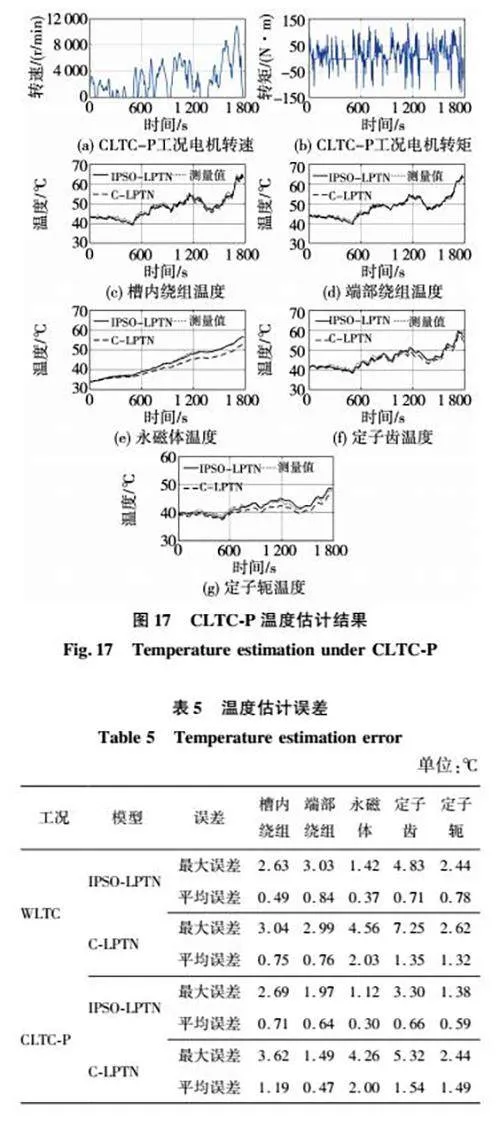
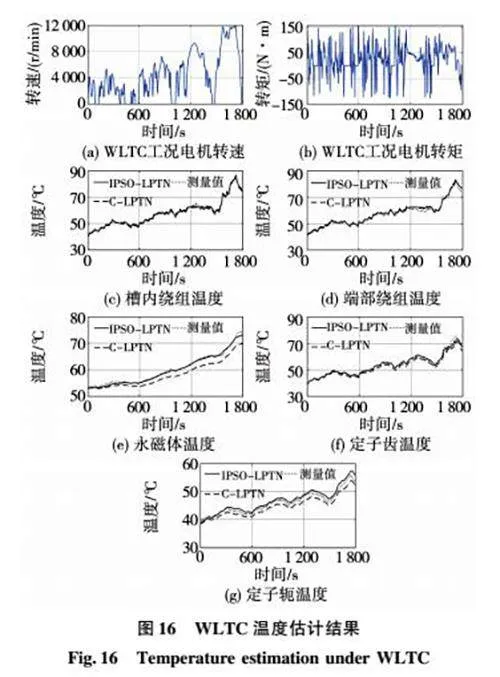
两种典型的综合驾驶工况，全球轻型车测试循环（word"wide harmonized light duty test cycle，WLTC）和中国轻型汽车测试循环（China light"duty vehicle test cycle"passenger，CLTC"P），结果分别如图16、图17所示，电机转速、转矩历程，分别如图16（a）、图16（b）和图17（a）、图17（b）所示。槽内绕组、端部绕组和永磁体温度分别如图16（c）、图16（d）、图16（e）和图17（c）、图17（d）、图17（e）所示。总体上，IPSO"LPTN 比C"LPTN 能够更好的吻合台架实验测量值。

为对模型的性能进行评价，本文运用了以下2个评价指标：平均绝对误差（mean square error，MAE）和最大绝对误差（max absolute error，MaxE）。

MAE的计算公式如下：

MAE=1N∑Ni=1|yi－y^i|。（14）

式中：yi为实验数据的测量值；y^i为模型估计输出值；N为实验数据总的样本数量。

MaxE的计算公式如下：

MaxE=min1≤i≤N|yi－y^i|。（15）

两种综合工况下，各节点的最大误差和平均误差如表5所示。WLTC工况的最大误差节点为定子齿，IPSO"LPTN的最大误差比C"LPTN减少334%；IPSO"LPTN的平均误差比C"LPTN减少486%。CLTC"P工况的最大误差节点为定子齿，IPSO"LPTN的最大误差比C"LPTN减少380%；IPSO"LPTN的平均误差比C"LPTN减少571%。可见，本文提出的IPSO参数辨识方法，显著提升了LPTN模型对复杂综合工况的适应性。

5 结 论

以永磁同步电机的实时温度模型为研究对象，针对LPTN模型未知参数较多、辨识算法难收敛的问题，提出迭代式粒子群优化辨识框架，分三步辨识共计22个参数。第一步利用无损耗的电机停转、冷却工况实验数据，辨识热阻、热容。第二步利用基转速以下的多工况实验数据，辨识电机损耗。第三步利用全转速范围的多工况实验数据，辨识绕组涡流系数，并修正气隙热阻。将辨识的参数值应用于全球轻型车测试循环工况和中国轻型汽车测试循环工况的永磁同步电机台架实验，结果表明，基于迭代式粒子群优化的参数辨识方法显著降低了LPTN模型的温度预测误差。本文的研究可用于提高永磁同步电机实时温度估计精确度，也可为电机高精确度控制、故障诊断和可靠性设计提供参考。但是，本文采用的辨识算法较复杂，尚不能满足实时辨识的需求。提高辨识算法的实时性、将参数辨识、温度估计与电机闭环控制耦合，是未来的研究方向。

参 考 文 献：

［1］"靳永春，陈俐，邹宇晟，等.永磁同步驱动电机温度场研究进展综述［J］.电气传动， 2023， 53（1）： 28.

JIN Yongchun， CHEN Li， ZOU Yusheng， et al. Review on research progress of PMSM temperature field ［J］. Electric Drive， 2023， 53（1）： 28.

［2］"CALIN M， HELEREA E. Temperature influence on magnetic characteristics of NdFeB permanent magnets ［C］//7th International Symposium on Advanced Topics in Electrical Engineering （ATEE）， May 12-14，2011，Bucharest，Romania.2011：1-6.

［3］"DU Guanghui， XU Wei， ZHU Jianguo， et al. Effects of design parameters on the multiphysics performance of highspeed permanent magnet machines ［J］. IEEE Transactions on Industrial Electronics， 2020， 67（5）： 3472.

［4］"FAN Xinggang， ZHANG Bin， QU Ronghai， et al. Comparative thermal analysis of IPMSMs with integralslot distributedwinding （ISDW） and fractionalslot concentratedwinding （FSCW） for electric vehicle application ［J］. IEEE Transactions on Industry Applications， 2019， 55（4）： 3577.

［5］"FAN Xinggang， LI Dawei， QU Ronghai， et al. Water cold plates for efficient cooling： verified on a permanentmagnet machine with concentrated winding ［J］. IEEE Transactions on Industrial Electronics， 2020， 67（7）： 5325.

［6］"李伟业，吴江权，王春燕，等.电动汽车用永磁同步电机温升计算不同方法对比分析［J］.防爆电机， 2019， 54（1）： 14.

LI Weiye，WU Jiangquan， WANG Chunyan， et al. Comparison and analysis on different temperaturerise calculation methods of PMSM for electric vehicles ［J］. ExplosionProof Electric Machine， 2019， 54（1）： 14.

［7］"SCEMA C， NATEGH S， BOGLIETTI A， et al. A hybrid thermal modeling method for traction motors used in dutycycles ［C］// 2019 IEEE International Electric Machines amp; Drives Conference （IEMDC）， May 12-15， 2019， San Diego， America. 2019： 2132-2137.

［8］"KIRCHGASSNER W， WALLSCHEID O， BOCKER J. Estimating electric motor temperatures with deep residual machine learning ［J］.IEEE Transactions on Power Electronic，2021，36（7）： 7480.

［9］"LEE J， HA J. Temperature estimation of PMSM using a differenceestimating feedforward neural network ［J］. IEEE Access， 2020， 8： 130855.

［10］"李和明，李俊卿.电机中温度计算方法及其应用综述［J］.华北电力大学学报， 2005， 32（1）： 1.

LI Heming， LI Junqing. Review on temperature computation and application in electric machines［J］. Journal of North China Electric Power University， 2005， 32（1）： 1.

［11］"刘文娟，潘超，米俭.永磁式同步电机热分析研究综述［J］. 东北电力大学学报， 2017， 37（2）： 93.

LIU Wenjuan， PAN Chao， MI Jian. Loss and thermal study review of permanent magnet synchronous machines ［J］. Journal of Northeast Electric Power University， 2017， 37（2）： 93.

［12］"靳永春. 永磁同步电机温度场测量与建模研究 ［D］. 上海： 上海交通大学， 2021.

［13］"CHIN J W， HWANG S W， PARK H J， et al. Thermal analysis and verification of PMSM using LPTN considering mechanical components and losses ［C］//2018 XIII International Conference on Electrical Machines （ICEM）， September 3-6， 2018， Alexandroupoli， Greece. 2018： 1323-1329.

［14］"ZHANG Shukuan， ZHENG Ping， YU Bin， et al. Thermal analysis and experimental verification of a staggeredteeth transverseflux permanentmagnet linear machine ［J］. IET Electric Power Applications， 2018， 12（7）： 1048.

［15］"ELREFAIE A M， HARRIS N C， JAHNS T M， et al. Thermal analysis of multibarrier interior PM synchronous machine using lumped parameter model ［J］. IEEE Transactions on Energy Conversion， 2004， 19（2）： 303.

［16］"FAN Jinxin， ZHANG Chengning， WANG Zhifu， et al. Thermal analysis of permanent magnet motor for the electric vehicle application considering driving duty cycle ［J］. IEEE Transactions on Magnetics， 2010， 46（6）： 2493.

［17］"SHI Wei， ZHOU Xuan. Online estimation method for permanent magnet temperature of high‐density permanent magnet synchronous motor ［J］. IEEJ Transactions on Electrical and Electronic Engineering， 2020， 15（5）： 751.

［18］"ZHANG Hengliang， GIANGRANDE P， SALA G， et al. Thermal model approach to multisector threephase electrical machines ［J］. IEEE Transactions on Industrial Electronics， 2021， 68（4）： 2919.

［19］"WALLSCHEID O， BOCKER J. Global identification of a loworder lumpedparameter thermal network for permanent magnet synchronous motors ［J］. IEEE Transactions on Energy Conversion， 2016， 31（1）： 354.

［20］"冯茜，李擎，全威，等.多目标粒子群优化算法研究综述［J］.工程科学学报， 2021，43（6）：745.

FENG Qian， LI Qing， QUAN Wei， et al. Overview of multiobjective particle swarm optimization algorithm［J］. Chinese Journal of Engineering， 2021，43（6）：745.

［21］"谢承旺，邹秀芬，夏学文，等.一种多策略融合的多目标粒子群优化算法［J］.电子学报，2015，43（8）：1538.

XIE Chengwang， ZOU Xiufen， XIA Xuewen， et al. A multiobjective particle swarm optimization algorithm integrating multiply strategies ［J］. Acta Electronica Sinica， 2015，43（8）：1538.

［22］"于慧，王宇嘉，陈强，等.基于多种群动态协同的多目标粒子群算法［J］.电子科技，2019，32（10）：28.

YU Hui，WANG Yujia，CHEN Qiang， et al. Multiobjective particle swarm optimization based on multipopulation dynamic cooperation ［J］. Electronic Science and Technology， 2019，32（10）：28.

［23］"LI Jinzhou， CHEN Weineng， ZHANG Jun， et al. A parallel implementation of multiobjective particle swarm optimization algorithm based on decomposition ［C］// 2015 IEEE Symposium Series on Computational Intelligence， December 7-10， 2015， Cape Town， South Africa. 2015： 1310-1317.

［24］"PENG Guang， FANG Yangwang， PENG Weishi， et al. Multiobjective particle optimization algorithm based on sharinglearning and dynamic crowding distance［J］.Optik，2016，127（12）：5013.

［25］"ZHANG Zhuoran， YU Li， SUN Li， et al. Iron loss analysis of doubly salient brushless DC generators ［J］. IEEE Transactions on Industrial Electronics， 2015， 62（4）： 2156.

［26］"LI Mengdi， HUANG Sheng， WU Xuan， et al. A virtual HF signal injection based maximum efficiency per ampere tracking control for IPMSM drive ［J］. IEEE Transactions on Power Electronics， 2020， 35（6）： 6102.

［27］"夏长亮，李帆，王慧敏，等.基于铁耗在线计算的最小损耗预测电流控制方法［J］.中国电机工程学报，2018，38（1）：266.

XIA Changliang， LI Fan， WANG Huimin， et al. Loss minimization predictive current control based on iron loss online calculation［J］. Proceedings of the CSEE， 2018， 38（1）： 266.

［28］nbsp;SUN Tianfu， WANG Jiabin， GRIFFO A， et al. Active thermal management for interior permanent magnet synchronous machine （IPMSM） drives based on model predictive control ［J］. IEEE Transactions on Industry Applications， 2018， 54（5）： 4506.

［29］"KRAL C， HAUMER A， LEE S B. A practical thermal model for the estimation of permanent magnet and stator winding temperatures［J］.IEEE Transactions on Power Electronics，2014，29（1）：455.

［30］"姚耀中，徐玉如.粒子群优化算法分析［J］.哈尔滨工程大学学报， 2007， 28（11）： 1242.

YAO Yaozhong， XU Yuru. Parameter analysis of particle swarm optimization algorithm ［J］. Journal of Harbin Engineering University， 2007， 28（11）： 1242.

［31］"沈艳，郭兵，古天祥.粒子群优化算法及其与遗传算法的比较［J］.电子科技大学学报， 2005， 34（5）： 696.

SHEN Yan， GUO Bing， GU Tianxiang. Particle swarm optimization algorithm and comparison with genetic algorithm ［J］. Journal of UEST of China， 2005， 34（5）： 696.

［32］"周俊，陈璟华，刘国祥，等.粒子群优化算法中惯性权重综述［J］.广东电力， 2013， 26（7）： 6.

ZHOU Jun，CHEN Jinghua， LIU Guoxiang， et al. Summary on inertia weight in particle swarm optimization algorithm ［J］. Guangdong Electric Power， 2013， 26（7）： 6.

［33］"随聪慧.粒子群算法的改进方法研究［D］.成都：西南交通大学， 2010.

［34］"方献军.硅钢温度场与应力场研究［D］.杭州：浙江大学， 2006.

［35］"杨世铭，陶文铨.传热学［M］.4版.北京：高等教育出版社， 2006.

［36］"魏秀芳，陈建宏，刘子江，等.金属热容量与温度关系的实验测定及理论研究［J］.西北师范大学学报， 2014， 50（2）： 43.

WEI Xiufang， CHEN Jianhong， LIU Zijiang， et al. Experimental measurement on the relation of metal heat capacity and temperature and comparing with theoretical results [J＼]. Journal of Northwest Normal University， 2014， 50（2）： 43.

（编辑：刘琳琳）

收稿日期： 2023-04-28

基金项目：上海交通大学“深蓝计划”基金（WH410260401/006）

作者简介：孟治金（1997—），男，硕士，研究方向为电机热模型、永磁同步电机设计与控制；

刘宇阳（1999—），男，博士研究生，研究方向为永磁同步电机温度估计；

陈 俐（1973—），女，博士，教授，博士生导师，研究方向为动力系统优化与控制、电驱装置建模与性能分析。

通信作者：陈 俐