基于无模型的PMLSM改进自适应滑模自抗扰控制

摘"要：

为了提高永磁直线同步电机的自抗扰控制的动态响应性能和抗干扰性能，增强系统整体的控制性能，提出了一种基于无模型控制的改进滑模自抗扰控制策略。首先，基于滑模变结构原理以及无模型控制理论对自抗扰控制器中的扩张状态观测器和非线性状态误差反馈进行优化，建立了超局部模型，采用非奇异快速终端滑模控制代替原有的非线性状态误差反馈，同时设计相应滑模面与扩张状态观测器相结合，提高观测器对扰动因素的观测精确度的同时增强控制器的动态响应性能和抗干扰能力。然后设计了改进指数趋近率，通过引入系统状态变量使得控制器可以进行自适应调节，进一步提高系统的控制性能。通过李雅普诺夫理论证明了控制策略的稳定性，仿真和实验结果表明，该控制策略相对传统的自抗扰控制器所具备的优越性。

关键词：永磁直线同步电机；无模型控制；非奇异快速终端滑模；改进滑模趋近率；自抗扰控制；改进扩张状态观测器

DOI：10.15938/j.emc.2024.01.014

中图分类号：TM359.4

文献标志码：A

文章编号：1007-449X（2024）01-0142-10

Improved adaptive sliding mode active disturbance rejection control for PMLSM based on modelfree theory

LI Zheng1，2，"ZHANG Zihao1，"WANG Kangtao1，"SUN Hexu1

（1.School of Electrical Engineering， Hebei University of Science and Technology， Shijiazhuang 050018， China;2.Institute of Electrical Engineering， Yanshan University， Qinhuangdao 066004， China）

Abstract：

In order to study and improve the dynamic response and antiinterference performance of the active disturbance rejection control of permanent magnet linear synchronous motor （PMLSM）， and enhance the overall control performance of the system， an improved sliding mode active disturbance rejection control strategy （ISMADRC） based on modelfree control was proposed. Firstly， the extended state observer （ESO） and nonlinear state error feedback （NLSEF） in the ADRC were optimized by the sliding mode variable structure principle and modelfree control theory. By establishing the ultralocal model and using nonsingular fast terminal sliding mode control to replace the traditional NLSEF， the corresponding sliding mode surface was designed to combine with the ESO. The dynamic response performance and antiinterference ability of the controller were enhanced by improving the observation accuracy of the observer to the disturbance factors. Then， based on this， an improved exponential reaching law was designed， and the controller can adjust itself by introducing system state variables， to further improve the control performance of the PMLSM system. The stability of the control strategy was proved by Lyapunov theory. Through simulation and experiment， it is confirmed that this control strategy has advantages over traditional ADRC.

Keywords：permanent magnet linear synchronous motor; modelfree control; nonsingular fast terminal sliding mode; improved exponential reaching law; active disturbance rejection control; improved extended state observer

0"引"言

永磁直线同步电机（permanent magnet linear synchronous motor，PMLSM）由于其具备较小的机械损耗，较大的直线推力以及高速等优点被广泛应用于高精密加工、物流运输等现代工业中的高精确度与强鲁棒性领域[1-2]。但是PMLSM控制系统中存在齿槽效应、边端效应和饱和效应等多种扰动因素，同时控制系统的状态间耦合严重，给系统的高性能控制带来较大的影响[3-4]。传统的PMLSM的控制方法大多数都采用PID控制器，PID控制器的运行可靠性较高，整体结构较为简单，同时可调参数较少，便于调节整定。但是PID控制在复杂的环境下容易受到外界干扰，导致系统整体的控制精确度降低和稳态性能下降[5]。

强鲁棒性和高精确度已经成为电机控制的发展趋势，目前主要的控制策略有模糊控制[6-7]、自抗扰控制[8-9]（active disturbance rejection controller，ADRC）和预测控制[10-11]等控制方法。PMLSM作为非线性多变量复杂系统，由于ADRC本身具备较强的鲁棒性，常选取ADRC应用于PMLSM系统中。文献[12]提出了一种最小二乘参数辨识的方法，通过对非线性函数进行改进，从而进一步提高ADRC的抗扰动能力。文献[13]提出了一种基于抗抖振因子函数的改进型函数来代替ADRC中的非线性函数，从而提高ADRC的控制性能。文献[14]通过调节函数大误差段增益对ADRC中的非线性函数进行改进，提高ADRC的抗扰性能，进一步改善系统的控制性能。

为进一步提高控制系统的控制性能，优化由于PMLSM中非线性扰动因素所导致的系统扰动，需要较为准确的对PMLSM运行过程中的负载进行观测。目前常见的扰动观测的方法主要分为扩张状态观测器[15-17]（extended state observer，ESO） 、滑模扰动观测器[18-19]、龙伯格扰动观测器[20-21]等。文献[22]通过采用级联的方法对于ADRC中的扩张状态观测器进行优化，在提高扰动估计精确度的同时，改善了系统的稳定性。文献[23]提出了一种用于ADRC的降阶扰动观测器，在简化系统结构的同时也保留了原有的优点。文献[24]对扩张状态观测器进行误差理论分析，采用改进非线性函数，进一步改善系统的控制性能。

本文以PMLSM控制系统为研究对象，设计一种基于无模型控制的改进滑模自抗扰控制策略。与传统的ADRC相比，该系统首先设计一种基于无模型的非奇异快速终端滑模来对非线性状态误差反馈（nonlinear state error feedback，NLSEF）进行优化，同时采用改进指数趋近率，增强PMLSM系统的控制性能并提高系统的稳定性。为进一步提高系统的抗干扰性能，采用滑模变结构原理及改进指数趋近率对ADRC中的ESO进行优化，提高观测器对于PMLSM系统中负载扰动项的观测精确度。仿真与实验中，通过变速运动和变负载运动对设计的控制策略与传统ADRC进行对比，表明其在PMLSM系统中具备较快的响应速度和较强的稳定性。

1"永磁直线同步电机数学模型

在旋转坐标系下，PMLSM的定子电压方程可以表示成如下的形式：

式中：v表示为直线电机运行速度；Rs表示为定子电阻；ud、uq、id、iq分别表示为PMLSM中d轴和q轴的电压分量和电流分量；Ld、Lq分别表示为PMLSM中的d轴和q轴的电感分量；ψf表示为直线电机的永磁体磁链；τ表示为直线电机中的极矩。

本文所使用的实验对象为表贴式PMLSM，满足L=Ld=Lq，因此直线电机的电磁推力方程可以简化为

式中：Fem表示PMLSM的电磁推力；pn表示PMLSM的极对数。

忽略空载推力时，直线电机的机械运动方程为

式中：m为直线电机中的动子质量；B为直线电机中的粘滞摩擦因数；f表示直线电机控制系统中的扰动项。联立式（2）和式（3）可以得到

其中：aM=3πpn2mτψf；bM=－Bm；cM=－1m。

2"传统自抗扰控制器的建立

标准的ADRC由3个部分构成，分别为ESO、NLSEF和跟踪微分器（tracking differentiator，TD）。PMLSM系统中速度环的ADRC系统原理图如图1所示。

3"基于无模型控制的改进NLSEF的设计

为增强ADRC的动态响应速度，进一步提高控制器的控制性能和抗干扰能力，本设计结合滑模变结构原理以及无模型理论对控制器中的NLSEF模块和ESO模块进行改进，并在此基础上设计了改进指数趋近率，从而进一步提高PMLSM系统的控制性能。

3.1"超局部模型的建立

基于无模型控制理论可将PMLSM系统的超局部模型表示为

式中：代表系统的导数阶数，其中满足≥1；y和u分别代表系统的输出和输入；G和σ分别表示系统中的未知因素以及可调参数。

为在实现较好的PMLSM系统的控制精确度的同时达到简化系统的目的，通过取=1建立一阶超局部模型来实现无模型控制的设计，由此可将式（9）改写为

由于采用传统的指数趋近率时，当运动点距离滑模面较远时，指数趋近率不能明显加快系统的收敛速度。当运动点趋于滑模面时，运动点的速度也不能自适应减小，从而使得系统的抖振现象加重。

本文通过在传统指数趋近率的基础上引入系统状态变量，提出了一种改进自适应指数趋近率，具体表达式为：

式中ε、k、λ、l均为大于零的常数。

式（16）在传统指数趋近率的基础上引入了基于系统状态变量的变指数项。当系统状态变量距离滑模面较远时，g（λ）和h（x1，x2）相对较大。则此时PMLSM系统可以较快的向滑模面靠近，进一步缩短了系统趋近于滑模面的时间。当系统状态变量靠近滑模面时，此时的趋近速率通过自适应调节趋近于零，使得系统状态变量x1和x2进入滑模面并向原点运动，进一步减小运动惯性，使得滑模抖振得到抑制。

基于上述理论分析可以看出，本文所设计的改进指数趋近率在具备传统指数趋近率的优点的同时，还缩短了系统的收敛时间，在减小系统抖振的同时提高了系统的控制性能。

为进一步改善PMLSM系统的控制性能，将改进指数趋近率中的符号函数替换为双曲正切函数。将式（13）、式（15）和式（16）联立可得基于无模型的改进NLSEF的控制律为：

3.3"改进NLSEF的稳定性分析

为分析本文所设计的基于无模型的改进NLSEF的稳定性，建立如下正定函数作为李雅普诺夫函数

由上式可知，本文所设计的改进NLSEF满足李雅普诺夫第二稳定性理论。进一步可知，在有限时间内，改进NLSEF模块中的状态变量均可以稳定的滑模运动收敛至滑模面。

4"改进ESO模块建立及稳定性分析

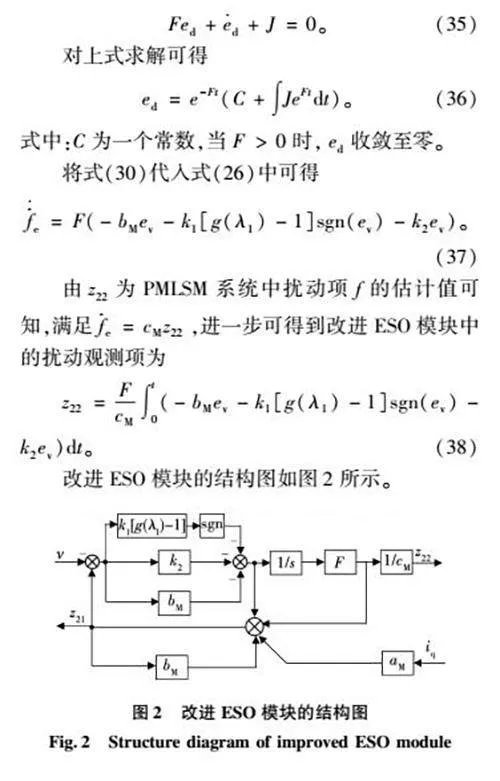
本章节设计了一种改进ESO模块，通过结合滑模变结构理论来增强观测器对于PMLSM系统中的扰动因素的观测精确度，从而进一步提高PMLSM系统的控制性能与抗干扰能力。

基于式（4），将fe=cMf视为扩张状态，则可得

改进ESO模块的结构图如图2所示。

5"仿真分析与实验验证

5.1"仿真分析

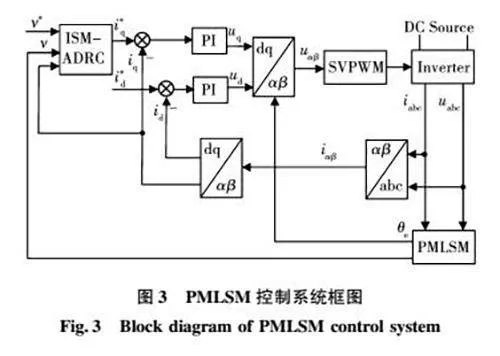
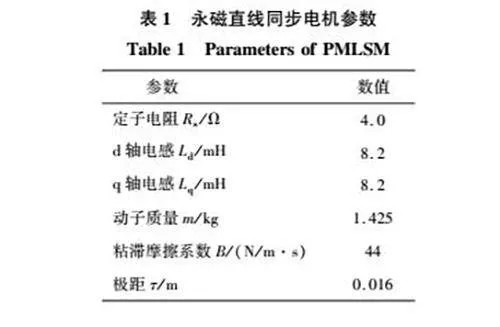
本文提出的基于无模型控制的PMLSM的改进自适应滑模自抗扰控制策略的系统框图如图3所示。根据表1所示的电机驱动参数通过MATLAB/Simulink建立相应的系统仿真模型，比较控制策略在变速运动和变负载运动情况下PMLSM系统的运行情况。

同时为进行较为详细的对比分析，本文共选取3种控制策略进行分析。分别为传统ADRC控制策略，基于无模型控制的改进滑模自抗扰控制器（sliding mode ADRC，SMADRC），以及应用改进指数趋近率的SMADRC（improved SMADRC，ISMADRC）。为确保对比测试的公平性，应用具备相同参数的电流环PI控制器以及TD模块。同时将滑模面参数及趋近率和改进ESO模块中的相同参数设置如下：α=80，β=0.3，p=21，q=19，g=47，h=41，ε=100，k=180，k1=15，k2=40，λ1=0.5，σ=130，F=80。3种控制策略中的其余参数设置如下所示。

ADRC中：β1=1 500，γ1=0.9，φ1=φ2=0.01，γ2=0.8，β01=2 500，β02=30 000，b=800。ISMADRC中：λ=0.3，l=10。

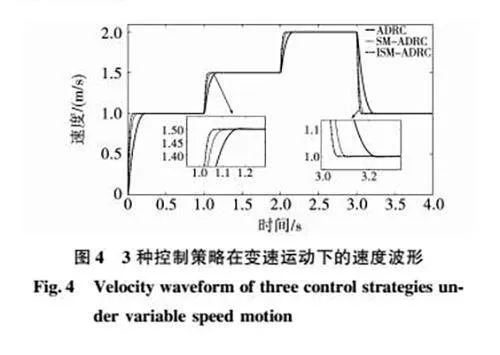
为检测所设计的控制策略在变速运动情况下的动态响应性能，在空载情况下，设定PMLSM系统的速度变化为1 m/s到1.5 m/s到2 m/s到1 m/s，速度每隔1 s变化一次。从图4可以看出，ISMADRC相对于传统ADRC和SMADRC具备较强的稳定性。所设计的ISMADRC在运行速度突增或突降的情况下都能够较快的到达目标速度，具备更快的动态响应能力。

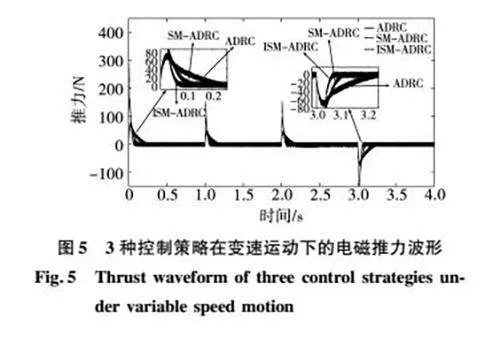
图5中体现了3种控制策略在变速运动情况下的空载推力波形。通过图5可以看出，本文所设计的ISMADRC相对其他两种控制策略在速度突然改变的情况下可以更迅速的进行调整，具备较小的调节时间以及较快的动态响应速度。

通过图4和图5中对变速运动下的PMLSM系统的仿真分析证明了本文所提出的ISMADRC具备较为优越的动态响应性能和控制性能。

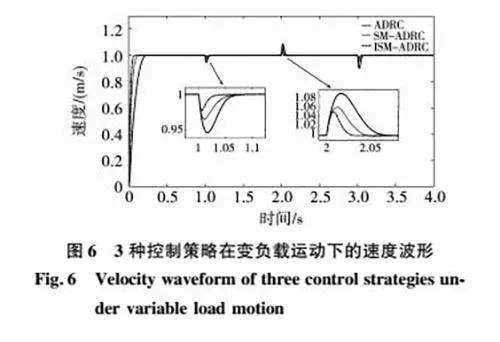
为测试本文中提出的3种控制策略在PMLSM系统中的负载突增和突降情况下的抗干扰能力，在给定运行速度为1 m/s的情况下，设置PMLSM系统的负载变化为60 N到90 N到100 N。图6中体现了3种控制策略在变负载运动情况下的速度波形变化。从图6中可以看出，本文所设计的ISMADRC和SMADRC在改进ESO模块的基础上与传统ADRC相比具备较强的抗干扰能力。相较于SMADRC，基于改进指数趋近率的ISMADRC自身的抗干扰能力和调节时间得到进一步改善。

基于以上结论表明本文所设计的ISMADRC具备较强的抗干扰能力。

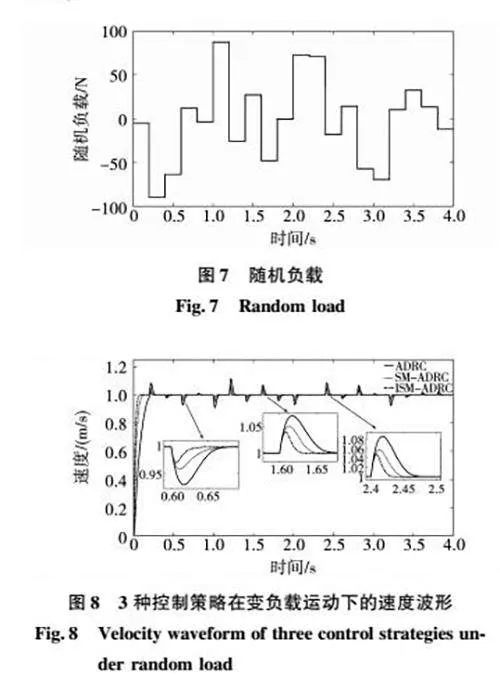
为对所设计的ISMADRC在复杂环境中的抗干扰能力和控制性能进行进一步的分析，将图7中所示的随机负载添加到3种控制策略中进行对比测试。图8中显示了当PMLSM系统的运行速度设置为1 m/s时，3种控制策略在随机负载情况下的运行速度对比。通过图8可以看出，本文所设计的ISMADRC在随机负载的情况下始终具备更小的扰动量，相对于其他两种控制策略在具备较快的动态调节速度的同时，还具有较强的抗干扰能力和控制性能。

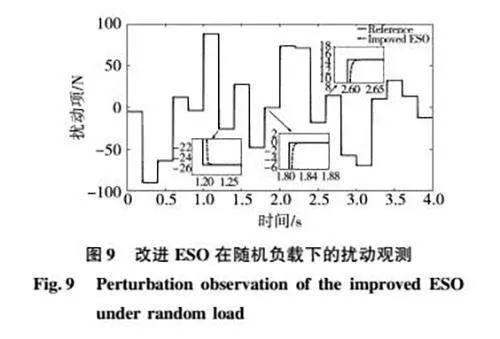
为对本文所设计的改进ESO模块对于PMLSM系统中的负载扰动的跟踪性能进行测试，图9中体现了改进ESO模块在随机负载下的负载扰动跟踪情况。通过图9可以看出本文所设计的ESMDO可以对PMLSM系统中的负载扰动进行较快的跟踪，并且具备较高的精确度。

可见本文所设计的改进ESO具备较强的负载扰动跟踪性能，进一步通过对系统中扰动量的高精确度的跟踪来提高PMLSM系统的抗干扰能力。

5.2"实验验证

在仿真分析的基础上，为进一步验证本文提出的ISMADRC的可行性与有效性，在实验室中搭建实验平台进行验证，通过浮点DSP芯片TMS320F28335来实现控制。实验平台如图10所示。在实验时，将编写好的控制系统主程序烧录到控制箱中，同时将控制板计算出的SVPWM信号传送到驱动模块中，从而控制PMLSM的运行。本实验对电机运行过程中变速运行和变负载运行情况下的速度波形和推力波形进行对比分析。实验中的电机参数和仿真一致。

由于实验中的检测环境与仿真中的理想环境不同，为了使直线电机更加稳定的运行，在轻载条件下，给定PMLSM的运行速度为0.6 m/s，在0.5 s时，将给定速度改变为0.8 m/s进行变速运行情况下的测试。

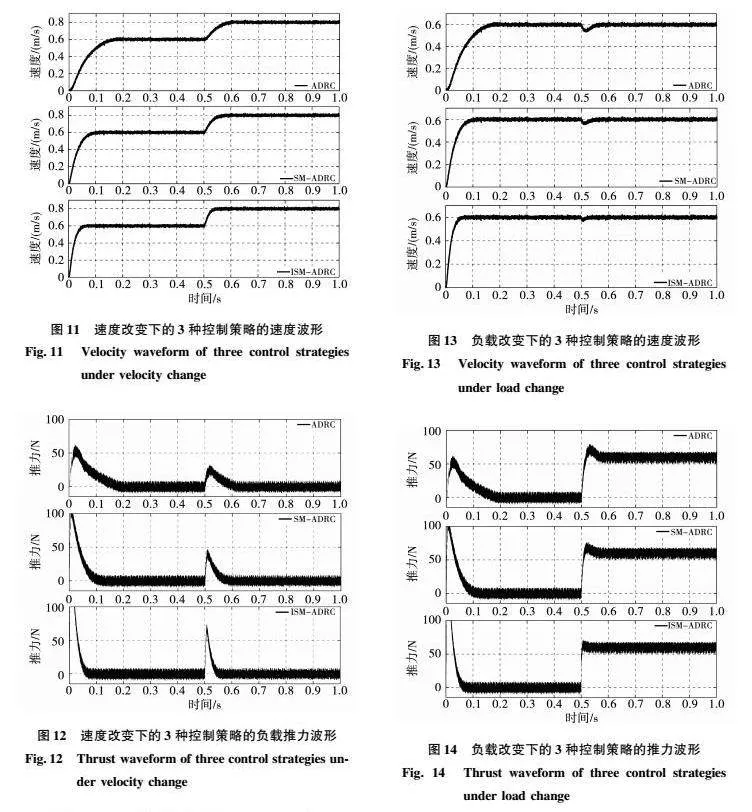
由图11可以看出，3种控制策略在两个运动阶段基本没有超调现象，表明3种控制策略均具备较好的控制性能。其中传统ADRC在两个运动阶段的调节时间分别为0.17 s和0.11 s。SMADRC在两个运动阶段的调节时间分别为0.11 s和0.06 s。ISMADRC在两个运动阶段的调节时间分别为0.07 s和0.045 s。结果表明，本文所设计的ISMADRC相较其他两种控制策略具有更小的调节时间，这反映了ISMADRC具有较强的动态响应能力和较高的控制性能。

图12为3种控制策略在运行速度变化后的推力波形变化。当运行速度发生变化时，ISMADRC的推力波形会在较短时间内调整为稳定状态。同时，相对于其他两种控制策略，ISMADRC控制策略具备更快的响应速度。

设定PMLSM的运行速度为0.6 m/s， 在0.5 s时给定60 N的负载，进行变负载运动下的测试。图13中体现了3种控制策略在变负载运动下的速度波形。图14中显示了3种控制策略在变负载运动下的推力波形比较。

由图13可以看出，在负载发生变化时，本文所设计的ISMADRC具备更小的扰动量以及更快的调节速度。同时相对于其他两种控制策略，ISMADRC能够在较短时间内将加入负载后的速度波形调整为稳定状态。

传统ADRC在负载变化时的调节时间和速度扰动量分别为0.07 s和0.064 m/s。SMADRC在负载变化时的调节时间和速度扰动量分别为0.045 s和0.043 m/s。ISMADRC在负载变化时的调节时间和速度扰动量分别为0.027 s和0.031 m/s。结果表示，本文的ISMADRC对比其他两种控制策略具备更快的响应速度和更小的扰动量，调节时间也更短，体现了ISMADRC具有较强的抗扰动性能和控制性能。

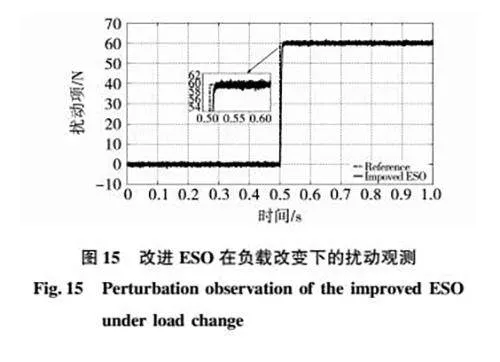
图14中显示了3种控制策略在负载变化下的推力波形比较。图15中显示了改进ESO模块在负载变化下观测到的系统扰动波形。

通过图14可见，当负载变化时，基于改进ESO模块的ISMADRC和SMADRC相对于传统ADRC具备更小的变化量。当负载变化后，本文所设计的ISMADRC的推力波形能够迅速恢复为稳定状态，与其他两种控制策略相比，ISMADRC具有更小的扰动变化量和更快的响应速度。

由图15可见，本文设计的改进ESO模块能够以较快的速度和较高的精确度对PMLSM系统中的负载扰动进行跟踪。结果表明，改进ESO模块对于系统中的负载扰动具备较强的跟踪性能，可以进一步改善PMLSM系统的抗干扰性能。

6"结"论

为增强PMLSM的动态响应性能和抗干扰性能，提高系统的控制性能，本文提出了一种基于无模型控制的改进滑模自抗扰控制策略。基于传统ADRC控制策略，该控制策略首先设计了一种基于无模型控制的非奇异快速终端滑模控制律来对NLSEF模块进行优化。同时采用改进指数趋近率，提高PMLSM系统的控制性能并增强系统的稳定性。为进一步提高PMLSM系统的抗干扰性能，本文采用滑模变结构原理及改进指数趋近率对ADRC中的ESO模块进行优化，实现观测器对于PMLSM系统中负载扰动因素的高精确度观测。在仿真和实验部分，将ISMADRC与SMADRC和ADRC控制策略在变速运动和变负载运动的情况下进行了比较。对比测试表明，所设计的ISMADRC的控制性能较强，具有较好的动态响应性能和较强的抗干扰能力。同时体现了改进ESO模块对于系统中负载扰动具备较强的跟踪性能。

参 考 文 献：

［1］"梁健强， 吴金洲， 魏巍. 基于辅助变量的永磁同步直线电机系统辨识研究[J]. 微电机， 2021， 54（11）： 52.

LIANG Jianqiang， WU Jinzhou， WEI Wei. Identification of permanent magnet synchronous linear motor system based on recursive instrumental variable method[J].Micromotors，2021，54（11）：52.

［2］"ZHENG Zhilei， ZHAO Jiwen， WANG Lijun， et al. Efficient optimization design method of PMSLM based on deep adaptive ridge regression with embedded analytical mapping function[J]. IEEE Transactions on Industrial Electronics，2022，69（8）：8243.

［3］"蒋钱， 卢琴芬， 李焱鑫. 双三相永磁直线同步电机的推力波动及抑制[J]. 电工技术学报， 2021， 36（5）： 883.

JIANG Qian， LU Qinfen， LI Yanxin. Thrust ripple and depression method of dual threephase permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society， 2021， 36（5）： 883.

［4］"李争， 肖宇， 孙鹤旭， 等. 基于速度前瞻的双轴直线电机交叉耦合控制策略[J]. 电工技术学报， 2021， 36（5）： 973.

LI Zheng， XIAO Yu， SUN Hexu， et al. Speed prospective based crosscoupling control strategy for dualaxis linear motor[J]. Transactions of China Electrotechnical Society，2021，36（5）：973.

［5］"PAN Zhenbao， DONG Fei， ZHAO Jiwen， et al. Combined resonant controller and twodegreeoffreedom PID controller for PMSLM current harmonics suppression[J]. IEEE Transactions on Industrial Electronics， 2018， 65（9）： 7558.

［6］"孙晓林， 沈宏亮， 杨立奎， 等. 基于模糊控制的三电机伺服控制系统特性研究[J]. 电子设计工程， 2022， 30（1）： 117.

SUN Xiaolin， SHEN Hongliang， YANG Likui， et al. Research on characteristics of threemotor servo control system based on fuzzy control[J]. Electronic Design Engineering， 2022， 30（1）： 117.

［7］"LIU Tianyi， LIU Zhiming， ZHU Fanglai. A nonlinear robust speed controller for dual nonidentical parallel PMSM system[J].IEEE Transactions on Power Electronics，2022，37（9）：10190.

［8］"WANG Bo， TIAN Minghe， YU Yong， et al. Enhanced ADRC with quasiresonant control for PMSM speed regulation considering aperiodic and periodic disturbances[J]. IEEE Transactions on Transportation Electrification， 2022， 8（3）： 3568.

［9］"LIN Ping， WU Zhen， LIU Kunzhi， et al. A class of linearnonlinear switching active disturbance rejection speed and current controllers for PMSM[J]. IEEE Transactions on Power Electronics， 2021， 36（12）： 14366.

［10］"李争， 安金峰， 肖宇， 等. 基于自适应观测器的永磁同步直线电机模型预测控制系统设计[J]. 电工技术学报， 2021， 36（6）： 1190.

LI Zheng， AN Jinfeng， XIAO Yu， et al. Design of model predictive control system for permanent magnet synchronous linear motor based on adaptive observer[J]. Transactions of China Electrotechnical Society， 2021， 36（6）： 1190.

［11］"ZHANG Zhen， WANG Zhichao， WEI Xile， et al. Spacevectoroptimized predictive control for dual threephase PMSM with quick current response[J]. IEEE Transactions on Power Electronics， 2022， 37（4）： 4453.

［12］"白国长， 娄轲， 马超群. 基于改进自抗扰PMSM位置控制[J]. 组合机床与自动化加工技术， 2022，64（10）： 74.

BAI Guochang， LOU Ke， MA Chaoqun. PMSM position control based on improved active disturbance rejection[J]. Modular Machine Tool amp; Automatic Manufacturing Technique， 2022，64（10）： 74.

［13］"张兰红， 李胜， 张卿杰. 永磁同步风电系统转速环自抗扰控制器设计[J]. 控制工程， 2022， 29（9）： 1645.

ZHANG Lanhong， LI Sheng， ZHANG Qinjie. Design of active disturbance rejection controller in speed loop for permanent magnet synchronous wind power generation system[J]. Control Engineering of China， 2022， 29（9）： 1645.

［14］"乔鑫宇， 周文雅， 吴国强. 自抗扰fal函数的改进及在无拖曳卫星中的应用[J]. 航天控制， 2022， 40（4）： 38.

QIAO Xinyu， ZHOU Wenya， WU Guoqiang. Fal function improvement of ADRC and its application in dragfree satellite［J］. Aerospace Control， 2022， 40（4）： 38.

［15］"WANG Yaoqiang， FENG Yutao， ZHANG Xiaoguang， et al. A new reaching law for antidisturbance slidingmode control of PMSM speed regulation system[J]. IEEE Transactions on Power Electronics， 2020， 35（4）： 4117.

［16］"吴宜， 梅珂琪， 丁世宏， 等. 基于扩张状态观测器的永磁同步电机转速环连续螺旋控制[J]. 广东工业大学学报， 2022， 39（5）： 112.

WU Yi， MEI Keqi， DING Shihong， et al. An extended state observer based continuous twisting control for PMSM speed regulation[J]. Journal of Guangdong University of Technology， 2022， 39（5）： 112.

［17］"QU Lizhi， QIAO Wei， QU Liyan. An extendedstateobserverbased slidingmode speed control for permanentmagnet synchronous motors[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics， 2021， 9（2）： 1605.

［18］"张荣芸， 周成龙， 时培成， 等. 基于自适应积分滑模与扰动观测的多PMSM同步控制[J]. 电力系统保护与控制， 2022， 50（20）： 127.

ZHANG Rongyun， ZHOU Chenglong， SHI Peicheng， et al. MultiPMSM synchronous control based on adaptive integral sliding mode and disturbance observation[J]. Power System Protection and Control， 2022， 50（20）： 127.

［19］"HOU Qiankang， DING Shihong， YU Xinhuo. Composite supertwisting sliding mode control design for PMSM speed regulation problem based on a novel disturbance observer[J]. IEEE Transactions on Energy Conversion， 2021， 36（4）： 2591.

［20］"薛峰， 储建华， 魏海峰. 基于龙伯格扰动观测器的永磁同步电机PWM电流预测控制[J]. 电机与控制应用， 2017， 44（11）： 1.

XUE Feng， CHU Jianhua， WEI Haifeng. PWM predictive current control of permanent magnet synchronous motor based on luenberger disturbance observer[J]. Electric Machines amp; Control Application， 2017， 44（11）： 1.

［21］"WU Jian， ZHANG Junda， NIE Baochang， et al. Adaptive control of PMSM servo system for steeringbywire system with disturbances observation[J]. IEEE Transactions on Transportation Electrification， 2022， 8（2）： 2015.

［22］"朱良红， 张国强， 李宇欣， 等. 基于级联扩张观测器的永磁电机无传感器自抗扰控制策略[J]. 电工技术学报， 2022， 37（18）： 4614.

ZHU Lianghong， ZHANG Guoqiang， LI Yuxin， et al. Active disturbance rejection control for position sensorless permanent magnet synchronous motor drives based on cascade extended state observer[J]. Transactions of China Electrotechnical Society， 2022， 37（18）： 4614.

［23］"高旭生， 李娟， 李生权， 等. 基于降阶自抗扰的永磁同步电机位置控制[J].组合机床与自动化加工技术，2022，64（8）：105.

GAO Xusheng， LI Juan， LI Shengquan， et al. Permanent magnet synchronous motor position control based on reducedorder active disturbance rejection[J]. Modular Machine Tool amp; Automatic Manufacturing Technique， 2022，64（8）： 105.

［24］"封志鹏， 李白雅， 张宇祥. 自抗扰ESO改进及其在PMSM控制中的应用[J]. 微电机， 2022， 55（3）： 47.

FENG Zhipeng， LI Baiya， ZHANG Yuxiang. ESO improvement of ADRC and its application in permanent magnet synchronous motor[J]. Micromotors， 2022， 55（3）： 47.

［25］"AGHABABA M P， AKBARI M E. A chatteringfree robust adaptive sliding mode controller for synchronization of two different chaotic systems with unknown uncertainties and external disturbances[J]. Applied Mathematics and Computation， 2012， 218（9）： 5757.

（编辑：刘素菊）

收稿日期： 2023-03-08

基金项目：国家自然科学基金（51877070，51577048，51637001）；河北省自然科学基金（E2021208008）

作者简介：李"争（1980—），男，博士，教授，研究方向为特种电机及其控制、新型电力传动装置；

张梓豪（1999—），男，硕士研究生，研究方向为永磁同步直线电机控制技术；

王康涛（1998—），男，硕士研究生，研究方向为永磁同步直线电机控制技术；

孙鹤旭（1956—），男，博士，教授，博士生导师，研究方向为运动控制与新能源技术。

通信作者：李"争