电磁悬浮系统的改进线性自抗扰控制方法

摘"要：

单点电磁悬浮系统是常导电磁磁浮列车悬浮系统的关键控制单元。针对单点电磁悬浮系统因强干扰影响导致控制性能下降的问题，提出了一种改进型线性自抗扰控制（LADRC）方法。首先，基于电磁悬浮结构及原理建立了单点悬浮系统线性化模型，并对系统稳定性进行了分析。其次，基于自抗扰控制方法设计位置外环控制器以及基于PI调节器的电流内环控制器，对线性扩张状态观测器进行改进，设计两级级联的线性扩张状态观测器提高扰动估计精确度及速度，进而提高LADRC中扩张状态观测器对系统扰动的估计能力，并在频域上分析了改进型LADRC扰动估计性能和抑制能力的优越性。最后，搭建实验环境，对改进线性自抗扰控制方法的有效性进行验证。实验结果表明，所提的改进型LADRC不仅具有良好的位置跟踪性能，同时相比传统LADRC具有更强的抗扰动能力。

关键词：单点电磁悬浮系统；线性自抗扰控制；级联扩张状态观测器；观测精确度；频域分析；抗扰性能

DOI：10.15938/j.emc.2024.01.013

中图分类号：TM930.2

文献标志码：A

文章编号：1007-449X（2024）01-0131-11

Improved linear active disturbance rejection control method for electromagnetic levitation system

YANG Jie1，2，3，"YANG Xing1，2，3，"GAO Tao1，2，3，"HU Hailin1，2，3

（1.School of Electrical Engineering and Automation， Jiangxi University of Science and Technology， Ganzhou 341000， China；2.Institute of Permanent Maglev and Railway Technology， Jiangxi University of Science and Technology， Ganzhou 341000，China；3.Jiangxi Key Laboratory of Maglev Technology， Ganzhou 341000， China）

Abstract：

The singlepoint electromagnetic levitation system is the primary control unit of the electromagnetic suspension maglev trains. Aiming at the problem of system control performance degradation due to the influence of strong disturbances in singlepoint electromagnetic suspension systems， an improved linear active disturbance rejection control （LADRC） method was proposed. Firstly， based on the structure and principle of electromagnetic levitation， the linear model of the singlepoint levitation system was established and the stability of the system was analyzed. Secondly， the position outer loop controller based on active disturbance rejection control method and the current inner loop controller based on PI regulator were designed. After that， the linear extended state observer was improved， and a twostage cascaded linear extended state observer was designed to improve the accuracy and speed of disturbance estimation， so as to improve the disturbance estimation ability of the extended state observer in the system. The advantages of the improved LADRC in disturbance estimation performance and inhibition ability were analyzed in the frequency domain. Finally， an experimental environment was constructed to test effectiveness of the improved linear active disturbance rejection control method. The experimental results indicate that the proposed improved LADRC not only has good position tracking performance， but also has stronger antiinterference capability compared with the conventional LADRC.

Keywords：singlepoint electromagnetic levitation system; linear active disturbance rejection control; cascaded extended state observer; observation precision; frequency domain analysis; disturbance rejection performance

0"引"言

磁悬浮列车[1]凭借着低噪声、能耗少、无污染、转弯半径小等优势，被视为发展高速轨道交通制式的理想方案。作为未来打造中高速轨道交通运输网的有力竞争者，被给予极大的期待。电磁悬浮控制系统[2]作为磁悬浮列车的核心技术之一，其控制性能的好坏是磁悬浮列车安全稳定运行的关键。

目前，磁悬浮列车的电磁悬浮控制系统易受到内部干扰（悬浮质量变化、传感器温漂、电感参数变化等）和外部干扰（直线电机干扰、轨道不平顺等）影响，导致传统PID控制[3]显得捉襟见肘，需要动态的调整3个参数去应对不同工况。因此，探索一种有效继承PID控制精髓，同时兼具强抗扰性和鲁棒性等优势的控制策略，对于增强系统的抗扰能力，提高系统稳定性具有重要意义。

自抗扰控制[4]（active disturbance rejection control，ADRC）是由韩京清研究员率先提出并逐步完善形成的一种全新的控制策略，其核心思想是通过自抗扰控制器将系统未知部分和内外干扰估计并补偿消除，将系统变换成积分串联型进行控制，是一条有效解决上述磁悬浮列车在悬浮控制过程中存在的问题的途径。同时，针对非线性ADRC参数众多，调整困难的问题，高志强教授提出了线性自抗扰控制器[5]（linear active disturbance rejection control，LADRC），进一步推广了ADRC的研究与应用。在磁悬浮领域，何凌云等[6]对比验证了双环PID和双环ADRC控制，突出了ADRC控制性能的优越性；黄翠翠等[7]通过引入LADRC控制，有效提高了磁悬浮复合隔振系统在宽频带内的隔振效果。此外，ADRC先后被推广应用到电机驱动[8]、磁悬浮轴承[9]、整流变电[10]等等领域，表现出强大的算法适应性，特别是针对一些非线性、模型不确定系统。

另一方面，ADRC控制性能主要依赖于其内核的线性扩张状态观测器（linear extended state observer，LESO）对扰动的估计水准，但是经典的LADRC存在扰动估计不足，无法被快速抑制的缺点，易造成系统调节时间较长和超调量较大的问题。针对此类问题，国内外研究学者相继提出了诸多改进策略，李翁衡等[11]通过在LADRC设计中引入电磁轴承转子系统刚性模型，提高了系统在跨越临界转速时的振动抑制能力。周雪松等[12]将母线直流电压的实际微分量与观测微分量的误差引入传统LESO，减小了估计误差，增强了并网逆变器的抗扰性能。Yang Li等[13]将电压逆变器模型部分信息和负载电流作为已知扰动引入LESO，增强了系统抗干扰能力。Zhou Chen等[14]通过火电机组温度数据，构建ADRC相位补偿网络，提高了温度控制系统的响应速度。上述改进策略虽然提高了系统的性能，但改进后的LESO设计比较复杂，需要依赖于系统模型信息和增加测试点，不利于算法实现，造成工程应用困难。

综上所述，在传统LADRC基础之上，本文对LESO结构进行改进，提高其对系统总扰动的估计能力，并通过控制律进行消除干扰，进而提高悬浮控制系统的抗扰性能。文章结构可分为：1）建立单点悬浮系统线性化模型，采用串级控制的思想，对电流环设计PI控制器，提高电磁铁电流响应速度，并将系统近似降为二阶，然后对位置环设计LADRC控制器。2）在传统LADRC基础上引入级联结构对LESO进行改进，通过两级LESO来提高观测器对系统总扰动的观测精确度，从频域角度分析证明改进型LADRC对扰动的估计和抑制能力。3）通过仿真和在单点悬浮实物平台上进行抗扰对比实验，验证改进算法的有效性。

1"单点悬浮系统数学模型

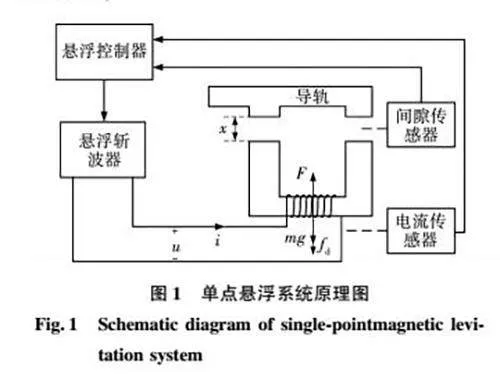
假设磁悬浮列车悬浮架能实现各悬浮点之间的完全解耦[15]，则可将列车的悬浮系统简化为一个单点悬浮系统进行建模分析。单点悬浮系统原理如图1所示。

图中：m为悬浮质量；x（t）为悬浮位置；F（x，i）为电磁铁悬浮力；fd（t）为扰动力；u（t）为电磁铁两端电压；i（t）为线圈电流。

结合悬浮动力学模型[16]分析，易得单点悬浮系统的基本模型：

式中：L为线圈电感；R为线圈电阻；μ0=4π×10-7为真空磁导率；A为电磁铁有效极面积；N为线圈匝数。

式中：F（x0，i0）为平衡点电磁力；i0和x0分别为平衡电流和平衡位置；Ki和Kx分别为电流刚度系数和位移刚度系数，其中：Ki=μ0AN2i0/2x20，Kx=μ0AN2i20/2x30。

由于电磁铁位置变化范围很小，线圈电感量在小范围内变换[18]不会影响控制分析，假设电磁铁线圈电感在位置变化过程中不变，则L（x）=L0=μ0AN2/x0；L0为平衡点电感。将式（1）和式（2）进行拉氏变换可得：

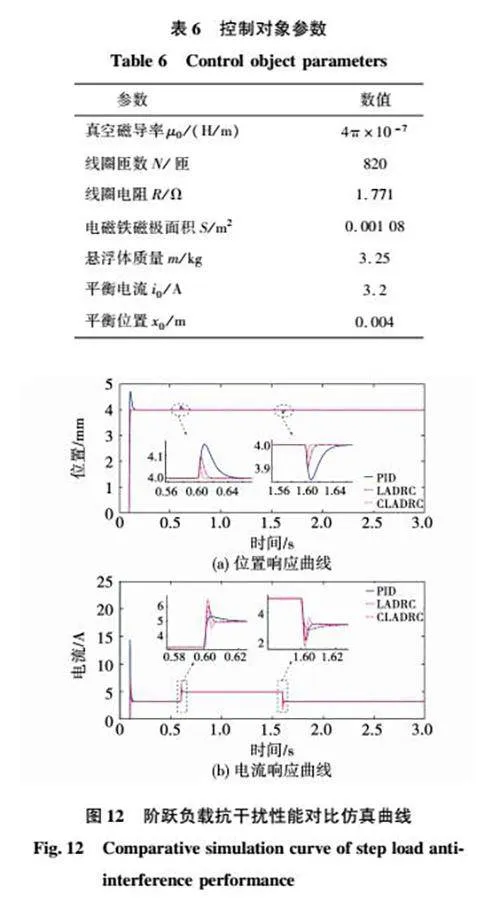
根据式（3）可得系统模型结构如图2所示。

由式（3）可得系统开环传递函数为

由系统特征方程（s2－Kx/m）（L0s+R）=0可知，系统特征值存在正实根，判断系统为一个三阶不稳定系统，需要设计控制器才能实现系统稳定。

2"单点悬浮系统控制设计

为了克服悬浮电磁铁的大电感效应[19]，本文沿用了传统磁悬浮技术中的串级控制结构[20]。将单点悬浮系统分解为电流内环子系统和位置外环子系统分别进行控制器设计。电流内环采取PI控制来提高电流响应速度，位置外环采取LADRC控制来实现系统稳定，并增强系统的抗扰性能。基于LADRC的单点悬浮系统双环控制结构如图3所示。

2.1"电流环控制器设计

根据式（3）可得电磁铁的电压与电流关系为

式中：KP为比例系数；KI为积分系数。

令PI控制系数分别为Kp=L0K，KI=RK，则UPI=（L0s+R）/s·K，电流环的闭环传递函数为

式中K为电流环增益。

若K的数值很大，则GI_cl≈1。通过引入式（7）所示PI控制器且将其控制参数K设置为非常大的数值后，可将系统由三阶近似降为二阶，电流环的控制参数将仅有一个K，这样设计不仅可以降低控制复杂度，同时还能保证电流响应速度。

2.2"基于改进型LADRC的位置环控制器设计

通过上面电流环控制器对系统近似降阶处理后，若设系统状态变量为x1=y（t），x2=y·（t），取控制输入u=－i（t），取扩张的系统状态变量x3=（Kx/m）x1+fd/m=f（x1，x2）+fd/m，作为系统被扩张的总扰动，f（x1，x2）为系统内扰，fd为外部扰动，令x·3=h和b0=b=Ki/m，则系统的状态方程为：

对位置环系统设计传统二阶LADRC控制器，其中，LESO设计：

式中：e1为观测误差；z1为输出x1的观测值；z2为x2的观测值；z3为系统扰动x3的观测值；b0为控制输入增益；u为控制量；β1、β2和β3为观测器增益。

传统线性状态误差反馈控制律：

u0=kp（r－z1）－kdz2；（10）

u=u0－z3b0。（11）

式中：r为设定值；kp和kd为反馈控制增益；u0是中间变量。

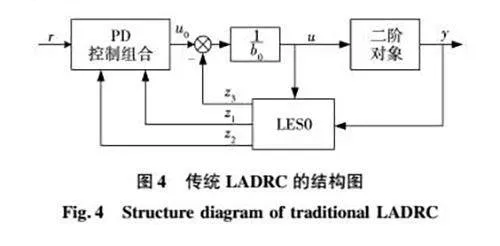
通过控制律将系统总扰动进行消除，可将位置外环系统变换为二阶积分串联形式：y··≈u0。传统LADRC的结构如图4所示。

传统LESO根据系统输出量和控制量来提取扰动信号，通过控制律来消除扰动，从而减小扰动对被控量的影响。即位置环LADRC控制器对扰动的估计精确度越高，相位滞后越小，则控制律将扰动消除地越精确，速度越快，控制器抗扰效果越好，扰动对位置被控量的影响越小。而传统LESO通常要先完成对x1的实时观测，再对x2和x3进行跟踪，这个过程会造成较大的跟踪误差[21]，导致扰动无法被完全消除。

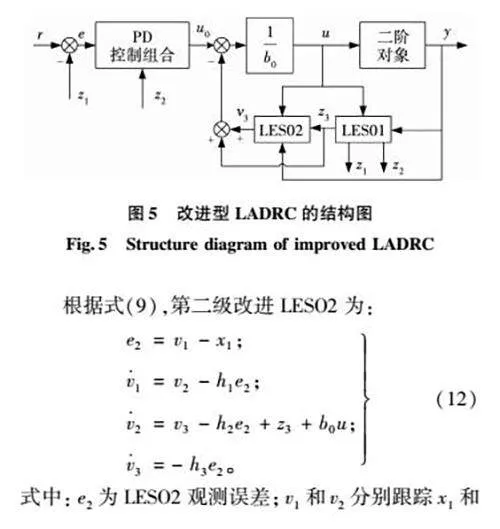
为进一步提高观测器对扰动的估计精确度，增强系统的抗扰性能，在传统LESO的基础上，通过改进LESO结构来提高扰动估计能力。通过配置LESO1的观测器增益高于LESO2的观测器增益，第一级LESO1对总扰动进行初步估计，获得系统部分扰动z3。为了提高干扰估计能力，将LESO1估计出来的z3视为已知部分，并实时反馈给第二级LESO2，通过LESO2同步估计剩余干扰部分v3=x3－z3，则z3+v3为最终估计出来的总扰动。两级并行LESO共同分担系统的扰动估计，对于获得部分系统扰动信息的LESO2，降低了LESO2的观测负担[22]，不仅加快了第二级LESO2的扰动估计速度，同时还提高了对扰动的估计精确度。改进型LADRC结构如图5所示。

式中：e2为LESO2观测误差；v1和v2分别跟踪x1和x2；v3为估计剩余扰动。h1，h2和h3为LESO2的观测器增益，采用与LESO1相同的观测器极点配置方法确定，为了简化分析，采取近似相等处理：

为了补偿两级LESO估计出来的总扰动，由式（11）可得控制律

根据文献[23]结论，配置观测器增益β1=3ωo，β2=3ω2o和β3=ω3o，线性状态误差反馈控制律参数kp=ω2c和kd=2ξωc。其中，ωo为观测器带宽，ωc为控制器带宽，取ξ=1，则改进型LADRC的控制参数将只有3个，即ωo、ωc和b0。

3"改进LADRC特性分析

3.1"干扰估计性能的分析

根据式（9）、式（11）、式（12）和式（14）可知z1、z2和z3分别关于输出y和控制输入u的传递函数[24]，同理可得到v1、v2和v3：

式中：ef1为传统LESO扰动估计误差；ef2为改进LESO扰动估计误差。

当输出y受到幅值为KT的阶跃干扰时，即y（s）=KT/s，代入式（16）和式（17）可得稳态估计误差：

由上式可知，通过配置合适的观测器增益，两种观测器均可以实现对系统输出阶跃扰动的无稳态误差观测。

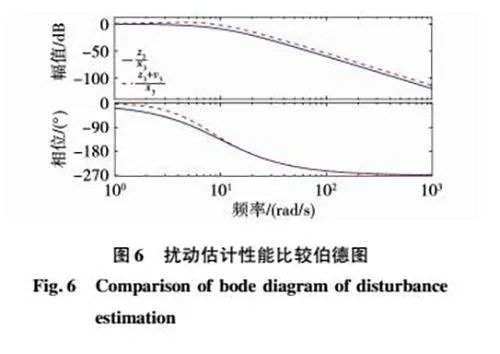
令ωo=20 rad/s，根据式（19）与式（20）可得到两种观测器的扰动估计比较伯德图，如图6所示。两种观测器对于由低频分量组成的扰动都可以很好的估计。在控制器有效带宽ωc=15 rad/s内，改进LESO的观测速度要快于传统LESO。假设系统总扰动被完全估计出来，则观测器对总扰动的幅值响应将等于1，而改进LESO在中高频段具有更高的幅值，说明其对扰动估计的更精确，有利于消除悬浮传感器反馈线路中的高频噪声干扰。

3.2"抗干扰性能分析

在理论上改进LESO具备良好的扰动估计能力，也为其提高抗扰性能提供了可能性，本小节将进一步探讨改进型LADRC的抗干扰性能。

将式（15）代入式（14）可得

根据式（21）可得基于改进型LADRC的位置外环系统结构图，如图7所示。

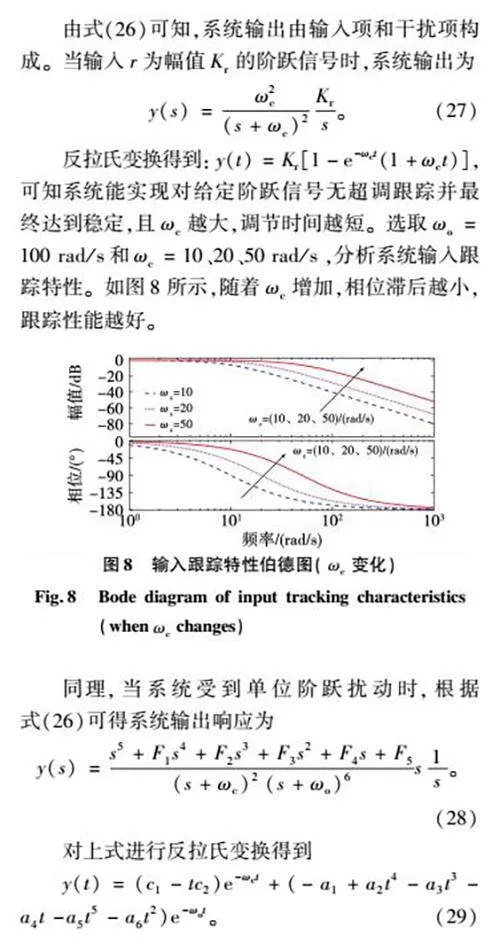
反拉氏变换得到：y（t）=Kr［1－e－ωct（1+ωct）］，可知系统能实现对给定阶跃信号无超调跟踪并最终达到稳定，且ωc越大，调节时间越短。选取ωo=100 rad/s和ωc=10、20、50 rad/s，分析系统输入跟踪特性。如图8所示，随着ωc增加，相位滞后越小，跟踪性能越好。

图8"输入跟踪特性伯德图（ωc变化）

Fig.8"Bode diagram of input tracking characteristics（when ωc changes）

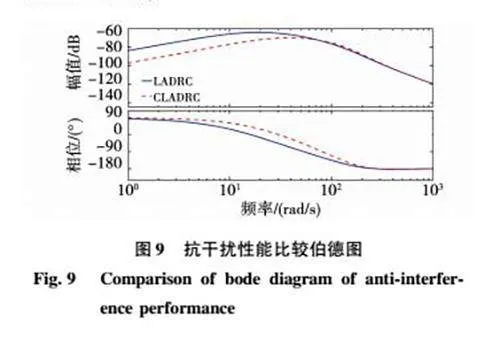
同理，当系统受到单位阶跃扰动时，根据式（26）可得系统输出响应为

由limt→∞y（t）=0可知，系统对扰动的稳态响应为0。选取ωo=150 rad/s和ωc=20 rad/s，比较两种算法的抗干扰性能，如图9所示。由于本文改进LADRC是对改进LESO采用了级联结构，在结果图中均简称为CLADRC。在系统控制器带宽ωc范围内，改进型LADRC的幅值要低于传统LADRC的幅值，说明由干扰信号产生的系统输出量占总输出量的比例更小，采用改进型LADRC提高了系统对干扰的抑制性能。

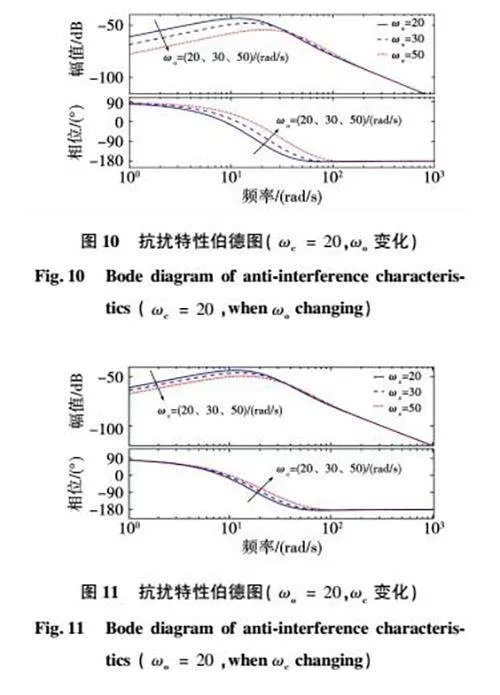
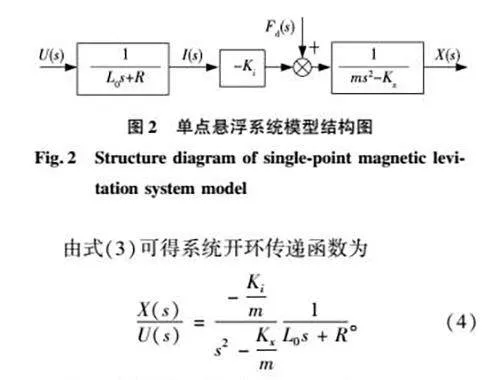
由式（26）可知，系统干扰项主要由ωo和ωc构成。在图10中，选取ωc=20 rad/s和ωo=20、30、50 rad/s，分析ωo变化对系统抗干扰性能的影响。在图11中，选取ωo=20 rad/s和ωc=20、30、50 rad/s，分析ωc变化对系统抗干扰性能的影响。由图10和图11可知，随着ωo和ωc增大，系统扰动输出增益减小，即增大ωo和ωc将增强系统的抗扰性能。

4"仿真与实验

4.1"仿真分析

为了验证所提控制方法的有效性，本文将改进型LADRC作为单点悬浮系统位置外环控制器，并与PID和传统LADRC进行抗扰对比实验。3种算法均结合相同PI控制参数（KP=354.2，KI=22.8）的电流环构成双环控制器。模型参数如表6所示。

图12为阶跃负载抗干扰性能对比仿真曲线，图12（a）和图12（b）分别为位置响应和电流响应曲线。在0.6 s给系统突加5倍阶跃负载扰动，持续1 s后，突减5倍阶跃负载扰动。由图可知，在PID控制下，系统经过50 ms调节时间重新回到平衡位置4 mm，达到新的平衡电流5.1 A，期间位置最大偏移量为0.16 mm。在传统LADRC控制下，调节时间为20 ms，位置偏移量为0.1 mm。而在改进型LADRC控制下，仅需10 ms调节时间就能恢复稳定且位置偏移量仅有0.05 mm。对比仿真结果可知，所提的改进型LADRC的抗扰性能要明显强于PID，而相比于传统LADRC，由于改进型LADRC对系统扰动的估计能力要优于传统LADRC，并通过线性状态误差反馈控制律及时地消除扰动后，可以使系统更快恢复平衡，并减小扰动对系统位置的影响。

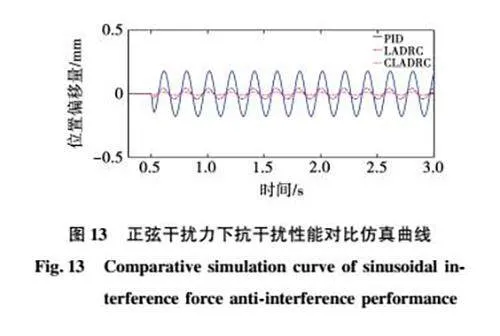
图13为正弦干扰力下的抗干扰性能对比仿真曲线。为了验证系统对周期性扰动力的抗扰能力，在0.5 s施加周期性325sin（10πt）N的干扰力，通过位置偏移量对比3种算法对周期性干扰的抗扰能力。由图可知，在PID控制下的系统位置波动范围为0.35 mm，在传统LADRC控制下的位置波动范围为0.082 mm，而在改进型LADRC控制下，位置波动范围仅有0.022 mm，位置量几乎不受到影响。对比仿真结果可知，针对周期性扰动，改进型LADRC具有更强的鲁棒性。

4.2"实验验证

为了进一步验证改进型LADRC的控制性能，在如图14所示的F轨单点悬浮实验台上面进行了实验。试验台由悬浮控制器（DSP TMS320F28335）、悬浮斩波器、24 V开关电源、悬浮台架、扰动施加装置、电涡流位置传感器、电流传感器组成。

实验一：设定位置的静态悬浮。

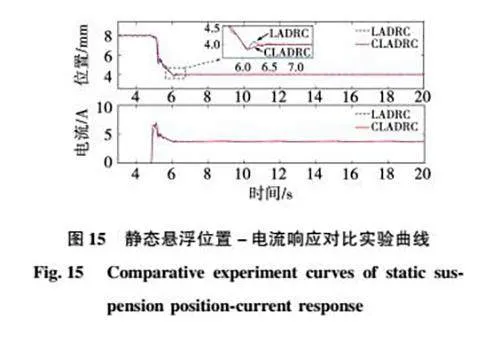
图15为悬浮电磁铁从初始位置8 mm到达设定位置4 mm的位置-电流响应对比曲线。为了防止起浮电流过大，实际给定为一个斜坡过渡信号，并采用相同的控制参数（ωo=70，ωc=10.2，b0=6）。由图可知，两种算法均存在0.14 mm的位置超调量，改进型LADRC的调节时间与传统LADRC基本相同，起浮阶段电流峰值均达到了6.8 A，到达平衡电流3.8 A稳定后波动较小。对比实验结果可知，对于设定跟踪信号，改进型LADRC继承了传统LADRC优秀的动态性能，具有跟踪速度快和超调量小的特点。可以实现快速无超调的跟踪且稳定后电流波动小，有利于保持系统的稳定性。

实验二：冲击性抗扰对比实验。

图16为扰动施加示意图。如图所示，采用质量为500 g的物体，分别从不同的高度以自由落体形式施加在悬浮架上，来验证控制器对不同强度的冲击性扰动的抗干扰性能。

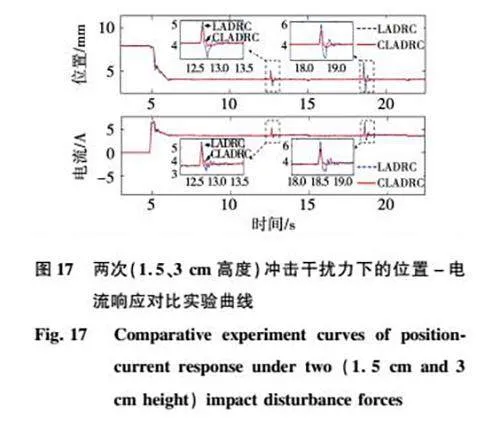
图17为在两次（1.5、3 cm高度）冲击干扰力下的位置-电流响应对比实验曲线。两种算法采取相同的控制参数（ωo=70，ωc=12.5，b0=6.5）。电磁铁在4 mm平衡位置稳定悬浮后，在12.5 s时刻附近，施加1.5 cm高度的冲击性干扰，持续3 s后停止作用。由图可知，若采用传统LADRC控制，系统在平衡位置上下波动范围为1.73 mm，经过1.1 s调节时间回到平衡位置，而采用改进型LADRC控制方法时，位置波动范围为0.8 mm，基本没有向上的超调量，系统仅需0.5 s调节时间，即可回到平衡位置。在18.5 s时刻附近，再次施加3 cm高度的冲击性干扰，同样持续3s，可见传统LADRC的位置波动范围为3.3 mm，调节时间为1.2 s，而改进型LADRC的位置波动范围为1.4 mm，调节时间为0.8 s。对比两次抗扰实验结果可知，相比于传统LADRC，采用改进型LADRC控制，系统位置偏移量平均减小了55%，调节时间平均缩短了43%。改进LESO增强了LADRC对扰动的观测精确度和观测速度，从而提高了位置环控制器的抗干扰性能。

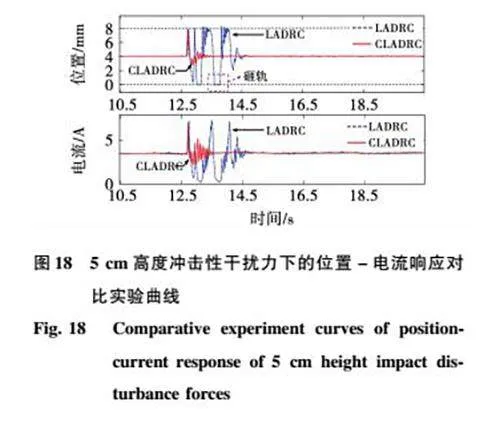
图18为在5 cm高度冲击性干扰力下的位置-电流响应对比实验曲线。由图可知，若采用改进型LADRC控制，系统在平衡位置上下波动范围为4.92 mm，经过1 s调节时间后可以重新恢复稳定。而当采用传统LADRC控制时，在相同干扰力作用下，发生了砸轨现象，消除干扰后系统才能重新恢复稳定。对比实验结果可知，改进型LADRC可使系统应对更高强度的冲击性干扰，提高了系统的鲁棒性。

5"结"论

为了提高磁悬浮列车电磁悬浮控制系统的抗扰能力，本文提出了一种基于级联线性扩张状态观测器的改进型LADRC控制方法，并得到如下结论：

1）采用两级级联的线性扩张状态观测器去估计系统扰动，可以减小观测器的估计负担，提高扰动估计精确度和速度，促进控制律更精确和快速的消除干扰，从而提高系统抗扰能力。

2）通过频域分析，改进型LADRC的扰动估计能力和干扰抑制能力要优于传统LADRC。仿真验证了改进型LADRC的有效性，进一步实验测试结果表明，相比于传统LADRC，改进型LADRC不仅具有良好的位置跟踪性能，同时还可显著增强系统在应对冲击性干扰时的抗扰性能，提高系统的稳定性。

参 考 文 献：

［1］"徐飞， 罗世辉， 邓自刚. 磁悬浮轨道交通关键技术及全速度域应用研究[J]. 铁道学报， 2019， 257（3）： 40.

XU Fei， LUO Shihui， DENG Zigang. Study on key technologies and whole speed range application of maglev rail transport[J]. Journal of the China Railway Society， 2019， 257（3）： 40.

［2］"马卫华， 罗世辉， 张敏， 等. 中低速磁浮车辆研究综述[J]. 交通运输工程学报， 2021， 21（1）： 199.

MA Weihua， LUO Shihui， ZHANG Min， et al. Research review on medium and low speed maglev vehicle[J]. Journal of Traffic and Transportation Engineering， 2021， 21（1）： 199.

［3］"KIM J， HA C W， KING G B， et al. Experimental development of levitation control for a highaccuracy magnetic levitation transport system[J]. ISA Transactions， 2020， 101： 358.

［4］"HAN J. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics， 2009， 56（3）： 900.

［5］"GAO Z. Active disturbance rejection control： from an enduring idea to an emerging technology[C]//2015 10th International Workshop on Robot Motion and Control （RoMoCo）， July 6-8， 2015，Poznan， Poland. 2015： 269-282.

［6］"何凌云. 磁悬浮系统的自抗扰控制［D］. 长沙：国防科学技术大学， 2007.

［7］"黄翠翠， 李晓龙， 杨洋， 等. 基于自抗扰技术的机械-电磁悬浮复合隔振控制[J]. 西南交通大学学报， 2022， 57（3）： 582.

HUANG Cuicui， LI Xiaolong， YANG Yang， et al. Mechanicalelectromagnetic suspension compound vibration isolation control based on active disturbance rejection technology[J]. Journal of Southwest Jiaotong University， 2022， 57（3）： 582.

［8］"ZHU J， GE Q. Traction system research of highspeed maglev train based on ADRC[C]//2019 22nd International Conference on Electrical Machines and Systems （ICEMS）， August 11-14， 2019， Harbin， China. 2019： 1-4.

［9］"WANG S， ZHU H， WU M， et al. Active disturbance rejection decoupling control for threedegreeoffreedom sixpole active magnetic bearing based on BP neural network[J]. IEEE Transactions on Applied Superconductivity， 2020， 30（4）： 1.

［10］"HE H， SI T， SUN L， et al. Linear active disturbance rejection control for threephase voltagesource PWM rectifier[J]. IEEE Access， 2020， 8： 45050.

［11］"李翁衡， 祝长生. 基于刚性转子模型辅助线性自抗扰的电磁轴承-柔性转子系统过二阶弯曲临界转速振动控制[J]. 中国电机工程学报， 2023，43（6）： 2413.

LI Wengheng， ZHU Changsheng. Vibration control of an active magnetic bearingflexible rotor system passing the second bending critical speed based on linear active disturbance control assisted by rigid rotor model[J]. Proceedings of the CSEE， 2023， 43（6）： 2413.

［12］"周雪松， 周泳良， 马幼捷， 等. 风电并网逆变器的改进型线性自抗扰控制[J]. 电气传动， 2022， 399（1）： 46.

ZHOU Xuesong， ZHOU Yongliang， MA Youjie， et al. Improved linear active disturbance rejection control of wind powergridconnected inverter[J]. Electric Drive， 2022， 399（1）： 46.

［13］"LI Y， QI R， DAI M， et al. Linear active disturbance rejection control strategy with known disturbance compensation for voltagecontrolled inverter[J]. Electronics， 2021， 10（10）： 1137.

［14］"CHEN Z， HAO Y S， SUN L， et al. Phase compensation based active disturbance rejection control for high order superheated steam temperature system[J]. Control Engineering Practice， 2022， 126： 105200.

［15］"马卫华， 胡俊雄， 李铁， 等. EMS型中低速磁浮列车悬浮架技术研究综述[J]. 西南交通大学学报， 2023， 58（4）： 720.

MA Weihua， HU Junxiong， LI Tie， et al. Technologies research review of electromagnetic suspension mediumlowspeed maglev train levitation frame[J]. Journal of Southwest Jiaotong University， 2023， 58（4）： 720.

［16］"SHI Y， MA W， LI M， et al. Research on dynamics of a new highspeed maglev vehicle[J]. Vehicle System Dynamics， 2022， 60（3）： 721.

［17］"王成杰， 伍星， 张静， 等. 中低速磁浮列车悬浮控制策略研究综述[J]. 电气自动化， 2019， 41（5）： 1.

WANG Chenjie， WU Xing， ZHANG Jing， et al. Summary of researches on levitation control strategies for low and medium speed maglev trains[J]. Electrical Automation， 2019， 41（5）： 1.

［18］"靖永志，王森，冯伟， 等. 基于电磁铁附加线圈的悬浮间隙检测方法研究［J］. 中国电机工程学报， 2023， 43（17）： 6807.

JING Yongzhi， WANG Sen， FENG Wei， et al. Research on the method of levitation gap detection based on electromagnet with an additional coil［J］. Proceedings of the CSEE， 2023， 43（17）： 6807.

［19］"蒋启龙， 梁达， 阎枫. 数字单周期电流控制在电磁悬浮系统中的应用[J]. 西南交通大学学报， 2019， 54（1）： 1.

JIANG Qilong， LIANG Da， YAN Feng. Application of digital onecycle control for current in electromagnetic suspension system[J]. Journal of Southwest Jiaotong University， 2019， 54（1）： 1.

［20］"WU Q， CUI N， ZHAO S， et al. Modeling and control of a six degrees of freedom maglev vibration isolation system[J]. Sensors， 2019， 19（16）： 3608.

［21］"姜仁华， 刘闯， 宁银行，等. 雷达伺服系统的高跟踪精确度改进型自抗扰控制器[J]. 电机与控制学报， 2019， 23（5）： 102.

JIANG Renhua， LIU Chuang， NING Yinhang， et al. Improved autodisturbance rejection controller of radar servosystem with high tracking accuracy[J]. Electric Machines and Control， 2019， 23（5）： 102.

［22］"张越杰， 张鹏， 冉承平，等. 扰动分离自抗扰控制在光电稳定平台上的应用[J]. 红外与激光工程， 2021， 50（10）： 244.

ZHANG Yuejie， ZHANG Peng， RAN Chengping， et al. Application of a disturbance separation active disturbance rejection control in photoelectric stabilized platform[J]. Infrared and Laser Engineering， 2021， 50（10）： 244.

［23］"李健， 谭文， 张彬文. 观测器带宽参数化的自抗扰控制[J]. 控制工程， 2022， 29（7）： 1181.

LI Jian， TAN Wen， ZHNAG Binwen. Observer bandwidth based active disturbance rejection control[J]. Control Engineering of China， 2022， 29（7）： 1181.

［24］"袁东， 马晓军， 曾庆含， 等. 二阶系统线性自抗扰控制器频带特性与参数配置研究[J]. 控制理论与应用， 2013， 30（12）： 1630.

YUAN Dong， MA Xiaojun， ZENG Qinghan， et al. Research on frequencyband characteristics and parameters configuration of linear active disturbance rejection control for secondorder systems[J]. Control Theory amp; Applications， 2013， 30（12）： 1630.

（编辑：刘素菊）

收稿日期： 2022-06-21

基金项目：国家自然科学基金（62063009）；江西省研究生创新专项资金（YC2020-B156）

作者简介：杨"杰（1979—），男，博士，教授，博士生导师，研究方向为磁悬浮控制；

杨"星（1997—），男，硕士研究生，研究方向为磁悬浮控制；

高"涛（1991—），男，博士研究生，研究方向为磁悬浮优化控制；

胡海林（1984—），男，博士，讲师，研究方向为磁悬浮控制、直线电机及其优化控制设计。

通信作者：胡海林