梯形Halbach交替极无铁心永磁同步直线电机特性分析与优化设计

摘"要：

针对无铁心永磁同步直线电机（PMLSM）存在推力波动问题以及磁极结构对永磁体利用率的影响，从结构方面着手，提出一种梯形Halbach交替极磁极结构的无铁心永磁同步直线电机，对Halbach阵列进行优化设计。首先通过有限元法对比在Halbach交替极、双层Halbach磁极与梯形Halbach交替极3种磁极结构中PMLSM的电磁性能，分别对气隙磁场谐波成分、空载反电动势、电磁推力以及推力体积比进行计算与对比。其次，采用等效磁化强度法定性分析磁极结构对电机出力性能的影响，并引入Kriging模型，结合多目标优化算法对关键参数进行优化以提高电机平均推力和推力体积比，降低推力波动，得到3个优化目标的Pareto前沿。最后，通过仿真分析验证设计方法的有效性以及电机性能的改善。结果表明：梯形Halbach交替极磁极结构永磁体利用率更高，具有实用价值；梯形Halbach交替极PMLSM能够有效抑制推力波动并保持在7%左右，适用于高精确度加工设备。

关键词：永磁同步直线电机；Halbach阵列；交替极；等效磁化强度法；Kriging模型；多目标优化

DOI：10.15938/j.emc.2024.01.016

中图分类号：TM351

文献标志码：A

文章编号：1007-449X（2024）01-0164-13

Characteristic analysis and optimization design of aircore permanent magnet linear synchronous motor with trapezoidal Halbach array consequentpole

MIAO Zhongcui1，2，"SU Yi1，"ZHANG Lei1，"ZHAO Xuan1，"LI Yan1

（1. School of Automation and Electrical Engineering， Lanzhou Jiaotong University， Lanzhou 730070，China; 2.Key Laboratory of OptoTechnology and Intelligent Control Ministry of Education， Lanzhou Jiaotong University， Lanzhou 730070， China）

Abstract：

Aiming at the problem of thrust ripple in aircore permanent magnet linear synchronous motor（PMLSM） and the influence permanent magnet structure on the utilisation of permanent magnets， a trapezoidal Halbach consequentpole of an aircore PMLSM with an optimised design was proposed for the Halbach array. Firstly， the electromagnetic performance of PMLSM in three pole configurations， Halbach array consequentpole， double Halbach array and trapezoidal Halbach array consequentpole， was compared by the finite element method. The air gap magnetic field harmonic components， backEMF， thrust and thrusttovolume ratio were calculated and compared respectively. Secondly， the equivalent magnetization intensity method was used to qualitatively analyze the effect of pole structure on the output performance of the motor. The Kriging model was introduced and combined with a multiobjective optimization algorithm to optimize key parameters to improve the average thrust and thrusttovolume ratio of the motor and reduce thrust ripple， and the Pareto front for the three optimization objectives was obtained. Finally， the results show that consequentpole is more efficient and saves manufacturing costs. Trapezoidal Halbach array consequentpole PMLSM effectively suppress thrust ripple and which remains at around 7%， and it is suitable for highprecision machining equipment.

Keywords：permanent magnet linear synchronous motor; Halbach array;consequentpole; equivalent magnetizationintensity method; Kriging model; multiobjective optimization

0"引"言

永磁同步直线电机（permanent magnet linear synchronous motor，PMLSM）具有推力密度高、响应速度快、传动效率高等优点，广泛应用于激光雕刻机、激光切割机等高精确度工业生产、半导体制造等领域[1-3]。但直线电机的推力波动会增加系统不稳定性，限制了加工精确度的提高[4-5]，并随着永磁体价格的上涨，导致制造成本增加，一定程度上限制了永磁同步直线电机应用。因此，对PMLSM推力性能优化、提高永磁体利用率的研究具有重要的理论与实践意义。

目前，对于抑制推力波动的研究主要从电机本体结构设计和控制策略两个方面进行[1]。在提高永磁体利用率方面，主要采用交替极的磁极排布方式，即利用导磁材料汇聚磁力线的特性，将部分永磁体用凸铁极代替构成混合磁极结构[6-7]。

通过电机本体结构设计来抑制推力波动主要有两个方面，分别为电机拓扑结构设计和结构参数组合优化设计。前者包括槽极配合的拓扑、永磁体形状的拓扑、绕组形状的拓扑、增加端部辅助极或辅助齿这4种类型[8]。在槽极配合的拓扑中，研究者通过改变电机的槽宽、槽深、绕组缠绕方式，将抑制推力波动的问题转化为抑制气隙磁场或电枢磁动势中谐波成分的问题[9-11]。这类方法能有效降低推力波动，但电机性能仍有较大的提升空间。除了槽极配合的拓扑，研究者还对电机其他结构拓扑进行了研究。文献[12]采用解析法分析磁场分布规律，通过V型三段磁极错位的磁极结构抵消推力波动中的谐波成分，达到抑制推力波动的效果。文献[13-14]分析推力波动规律，对动子端部的形状和辅助齿进行设计，削弱了端部效应对电机推力造成的不良影响。但在以上方法中，大部分模型的求解计算量大，对加工工艺要求较高，并且在一定程度上削弱了电磁推力。

在电机结构参数组合优化设计方面，文献[15-17]分别利用能量法、等效电路法和许-克变换法，从解析模型中得到电机系统响应与结构参数之间的关系，并对关键参数进行优化。但上述方法利用解析法建模，存在诸多假设条件，适合定性分析，不能进行高精确度计算。为了使模型计算更精确，文献[18-19]引入代理模型的计算方法，对样本数据库采用深度学习算法来建立高精确度计算模型，进而为优化算法提供高精确度模型基础。但在建立深度学习模型时，为保证高精确度，需要大量样本点数据，从而计算时间增加，优化效率降低，无法最大限度发挥代理模型的优点。

在提高永磁体利用率的研究中，用凸铁极替代部分永磁体构成交替极的磁极结构，虽然可以减少永磁体用量，但存在极间漏磁严重、降低电磁推力的问题。因此，文献[7]采用Halbach交替极（Halbach consequentpole，HCP）的磁极排布，弥补交替极结构漏磁严重的缺陷，但Halbach磁极阵列增加了强磁侧的磁场谐波分量，加剧了推力波动。而Halbach永磁阵列叠加是一个有效的解决方案，文献[20]采用双层Halabch（double Halbach，DH）磁极结构，单个永磁体为“凸”字型，但磁场谐波抑制效果有限，并且永磁体用量较大。

综上所述，电机设计与优化不仅要降低推力波动，还要保证电磁推力不降低，同时还要考虑永磁体利用率等问题。本文根据一种激光雕刻机的设备需求，从电机本体结构设计出发，设计一种梯形Halbach交替极永磁同步直线电机（trapezoidal Halbach consequentpole PMLSM，THCPPMLSM），其永磁体部分采用梯形Halbach阵列，用凸铁极替代部分永磁体形成梯形Halbach交替极。并在代理模型的基础上采用多目标优化算法对关键参数进行优化，在减少永磁体用量，提升电机出力性能的同时，最大化地利用仿真计算能力，提升优化效率。首先，根据文献[7]中的Halbach交替极、文献[20]中的双层Halabch磁极，来分别建立Halbach交替极永磁同步直线电机和双层Halbach永磁同步直线电机模型，与本文提出的THCPPMLSM在电磁性能上进行对比分析，初步证明提出结构的合理性。其次，对所提出的THCPPMLSM通过等效磁化强度法建立气隙磁场解析模型，依次建立平均推力、推力波动和推力体积比的解析模型，并选择极距、主永磁体宽度和梯形磁极斜面倾角为待优化的参数。然后，在优化参数设计范围内采用拉丁超立方抽样选取样本点[21]，通过有限元法计算样本点的响应值。接着，根据样本点以及响应值建立Kriging模型并与期望改进（expected improvement，EI）加点准则相结合，通过多种群遗传算法对模型进行优化，得到优化目标Pareto前沿。最后，根据优化参数在有限元仿真软件中建模，进行电磁性能比较和经济性分析，验证本文所提出THCPPMLSM与HCPPMLSM、DHPMLSM相比，在提高电机平均推力、提高推力体积比、降低推力波动以及实际应用价值等方面具有一定优势。

1"梯形Halbach交替极结构设计

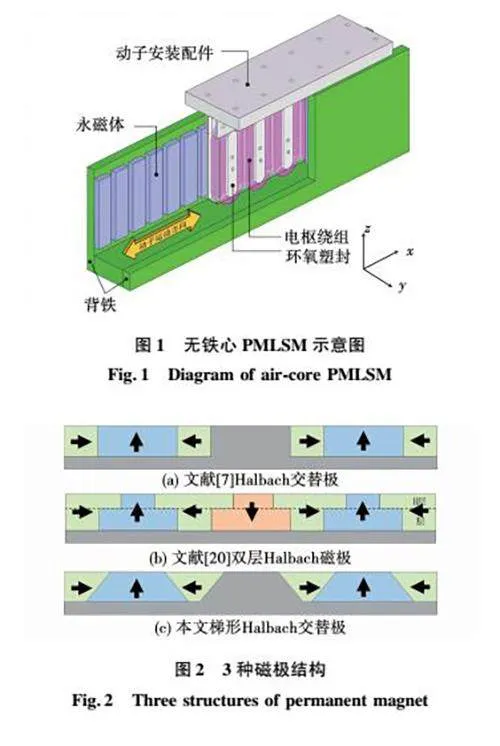
本文采用无铁心PMLSM，其运行时无齿槽力，适用于高精确度加工系统。无铁心PMLSM示意图如图1所示，初级部分的三相绕组被环氧树脂等非导磁材料塑封，次级部分采用双边对称的永磁体排布方式，形成类似“U”型结构对初级部分进行包裹。

1.1"磁极结构设计

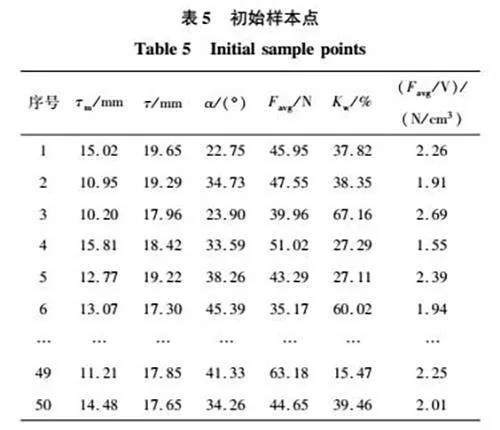
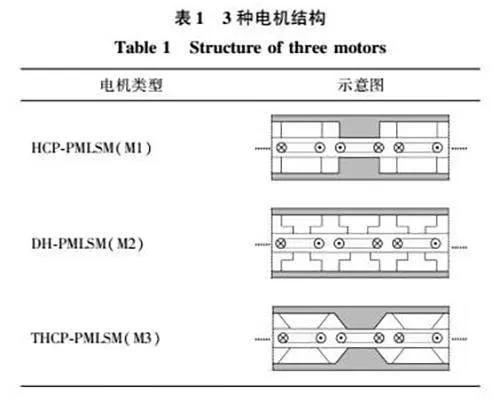
为减少塑封时的工艺复杂程度，电机初级绕组为单层矩形集中式绕组。次级部分一般采用径向充磁的矩形永磁体N极、S极交替排布，但这样不仅磁极间漏磁严重，而且永磁体用量大。本文提出梯形Halbach交替极磁极排布设计，每对磁极由一个梯形Halbach永磁体与一个凸铁极构成，永磁体与凸铁极极性相反。这样的磁极设计不仅能减少磁极交替排布的极间漏磁，同时也减少了永磁体用量。本文所提出磁极结构与文献[7]、文献[20]的磁极结构如图2所示。

1.2"THCPPMLSM电磁特性分析

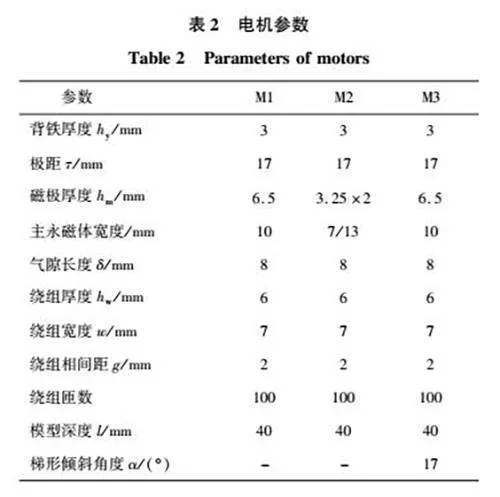
根据上述3种磁极结构，在有限元仿真软件中分别建立HCPPMLSM（M1）、DHPMLSM（M2）和THCPPMLSM（M3）3种电机模型，电机模型如表1所示。为保证对比公平性，3种电机单个磁极体积相同，额定电流和动子速度一致，其他参数如表2所示。根据3种电机模型对比分析静磁场状态、瞬态空载状态和负载状态下的电磁特性。

1）电机静磁场状态。

在Halbach阵列中，强磁侧的气隙磁通密度具有较多的谐波成分，会对电磁推力的稳定性造成不良影响。通过有限元分析得到3种电机气隙中心处的磁通密度分布曲线，如图3（a）所示，其中THCPPMLSM的磁通密度曲线最为平滑，比较接近正弦波形。同时还可以看到，两个交替极结构在永磁体用量相同的前提下，THCPPMLSM具有更高的磁通密度幅值。

为进一步验证，通过二维傅里叶分析可知，HCPPMLSM气隙中心处除了含有基波，同时还有其他谐波分量，其中5次谐波、9次谐波最为明显。DHPMLSM谐波抑制效果相比HCPPMLSM有所提升，而THCPPMLSM的谐波分量最少，表明其磁通密度谐波抑制能力在3种磁极结构中最佳，如图3（b）所示。

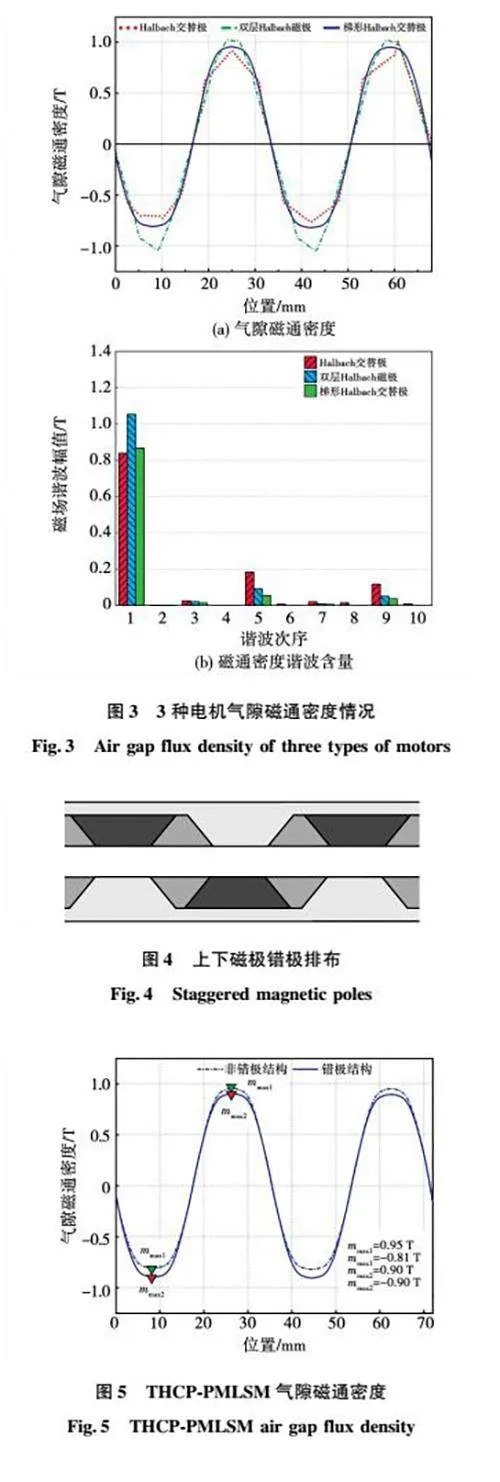
观察图3（a）中磁通密度上下幅值时可以发现，交替极结构存在明显的波形不对称现象，即正向幅值大于负向幅值。这种不对称现象是由于凸铁极未被永磁体完全磁化，导致永磁体产生的磁场大于凸铁极产生的磁场。为解决这一问题，采用图4所示上下错极的磁极排布结构，图5为THCPPMLSM错极后气隙磁通密度曲线。由图5可以看出，错极排布后正向气隙磁通密度幅值减小，负向气隙磁通密度幅值增大，且幅值都为0.9 T。

2）电机瞬态空载运行状态。

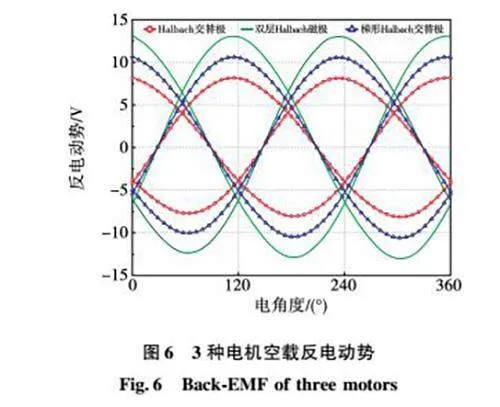
当动子运行速度为1.7 m/s，3种电机的空载反电动势如图6所示。DHPMLSM因永磁体用量最多而空载反电动势最大，以此为对比基准，则HCPPMLSM与THCPPMLSM的空载反电动势分别是基准值的62.2%（8.15 V）和80.9%（10.6 V）。在两个永磁体用量相同的交替极结构中，THCPPMLSM反电动势更高。

3）电机负载运行状态。

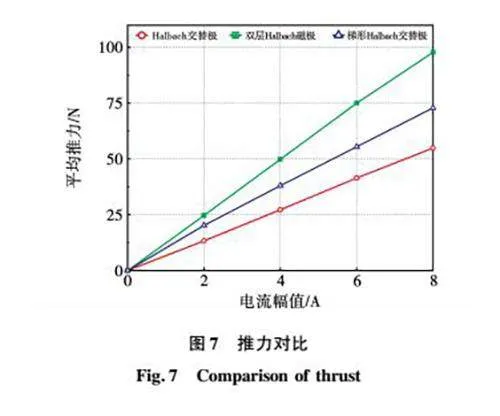
在不同电流激励工况下，各电机平均推力计算结果如图7所示。由图7可知，由于DHPMLSM永磁体用量最多其平均推力最大，其推力常数为12.53 N/A，以此为对比基准值。HCPPMLSM和THCPPMLS的推力常数分别是基准值的59.6%（7.47 N/A）和73.1%（9.16 N/A）。

推力体积比（永磁体利用率）也是重点考虑的一个性能参数[22]，定义为平均电磁推力与电机初级、次级耦合部分永磁体的体积之比。其中HCPPMLSM和THCPPMLSM初次级耦合部分的永磁体体积为DHPMLSM的69.6%，通过推力体积比的定义计算可知，在相同永磁体用量的情况下，THCPPMLSM推力体积比即永磁体利用率最高。

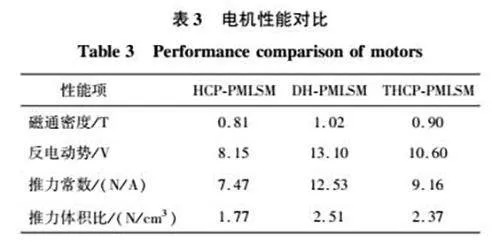
综上所述，3种电机性能对比如表3所示。可以看出，在相同永磁体用量的情况下THCPPMLSM比HCPPMLSM具有更好的性能表现。与DHPMLSM相比，由于THCPPMLSM减少永磁体用量，所以在电机性能上有一定的差距，因此将建立电机解析模型选择关键结构参数进行优化。

2"电机解析模型建立

通过解析模型可进一步分析THCPPMLSM响应与结构参数之间的关系。首先，采用等效磁化强度法建立层析模型，对气隙磁场进行分析，在此基础上建立了THCPPMLSM待优化性能的解析模型。

2.1"气隙磁场

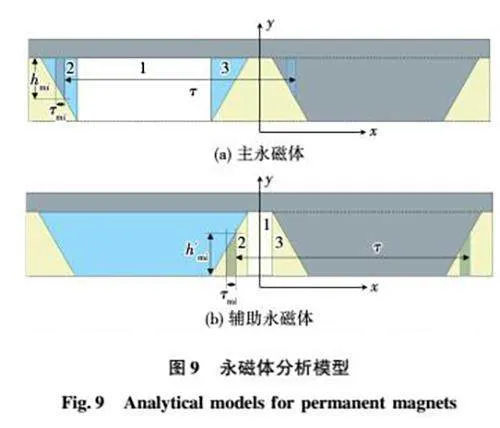
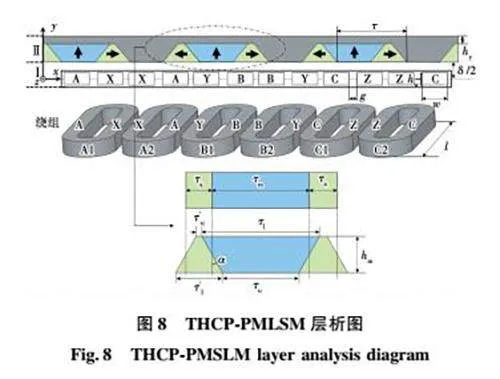
由于电机采用双边次级对称结构，只需对上半部分进行分析。永磁体产生的磁场，采用等效磁化强度法进行计算[23-24]，直线电机层分析模型以及结构参数如图8所示，此时绕组为无电流的空载状态，故将求解区域分为气隙区域与永磁体区域。

为了简化解析模型建立，对电机层分析模型做如下假设：

1）定子部分沿x轴方向无限延伸，忽略其边端效应。

2）z轴方向无磁场变化，不考虑横向边端效应，将模型进行二维分析。

3）凸铁极和背铁磁导率无穷大。

4）永磁体被均匀磁化。

考虑到梯形永磁体比矩形永磁体的边界条件更复杂，所以将梯形永磁体分为3个区域进行计算，如图9所示。区域1为矩形，区域2和区域3为直角三角形，其中单个直角三角形区域再近似细分为i个不同高度矩形的叠加，高度为hmi，宽度为τmi。最后通过叠加计算，即可得到梯形永磁体的磁通度。

通过等效磁化强度法计算永磁体的磁场，磁通密度矢量可以由矢量磁位得到，表达式为

根据Maxwell方程组，建立气隙区域Ⅰ的拉普拉斯方程和永磁体区域Ⅱ的泊松方程，即

式中：A→Ⅰ、A→Ⅱ为气隙区域的矢量磁位和永磁体区域的矢量磁位；M→为永磁体磁化强度空间分布函数。

Halbach阵列的磁化强度空间分布函数为

式中：Br为永磁体剩余磁化强度；μ0为空气磁导率；mn为仅包含奇次谐波的空间频率；αp为矩形永磁体宽度与极距的比值。

对于永磁体区域2和区域3的三角形永磁体，如图9所示，计算其细分的第i块矩形永磁体磁段，此时αp=τmi/τ，应满足如下边界条件：

b相绕组与c相绕组的感应电动势计算与上述过程相同，b、c相的感应电动势分别滞后a相2π/3、4π/3。

2.3"电磁推力以及推力波动

由于是无铁心动子，所以可忽略电枢反应的影响，采用空载感应电动势计算电磁推力，电磁推力可表示为

式中ia、ib、ic分别为三相绕组中的激励电流。当绕组中的激励电流为三相正弦交流电时，电磁推力表达式为：

式中：Fi为第i个采样点的电磁推力值；Favg为电磁推力平均值。

2.4"推力体积比

推力体积比表征电机中永磁体的利用率，定义为平均推力与电机初级、次级耦合部分永磁体的体积之比。初级、次级耦合部分永磁体体积为：

式中：Vm、Va分别为y方向充磁永磁体（主永磁体）和x方向充磁永磁体（辅助永磁体）的体积；p、q分别为永磁体数量；τm、τa分别为主永磁体和辅助永磁体宽度。

推力体积比为

3"关键结构参数选取

通过解析模型可知，Halbach阵列对电机推力品质有着重要影响。在电磁推力方面，Halbach阵列中的主永磁体起主导作用，调节主永磁体与辅助永磁体在Halbach阵列中的比例，可以优化电磁推力的表现。同时，由式（25）可知，辅助永磁体宽度的改变可以看作极距的调节。平均推力值随主永磁体宽度和极距变化如图10所示。

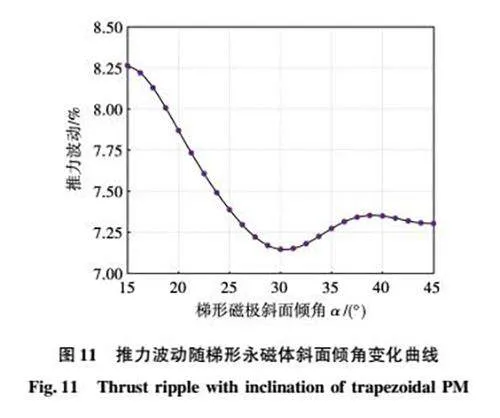
在推力波动方面，由解析模型分析可知，梯形永磁体斜面倾角与推力波动有关，推力波动与斜面倾角的关系如图11所示，随倾角增大，推力波动呈下降趋势。

在推力体积比方面，由式（26）可知，永磁体尺寸参数同时影响电磁推力以及推力体积比。永磁体厚度也是尺寸参数之一，但从图12中平均推力和推力体积比随永磁体厚度变化曲线可以看出，磁体厚度在5～10 mm内变化时，平均推力变化幅度仅3 N左右，且永磁体厚度增加反而降低了推力体积比，所以将永磁体厚度设为固定值。

为了使模型具有普适性，将主永磁体宽度、极距和梯形永磁体斜面倾角作为优化参数，其他参数设为固定值。根据设计尺寸和空间约束条件，优化参数以及设计范围如表4所示。

4"关键参数优化

本文以THCP-PMLSM的平均推力、推力波动和推力体积比为优化目标。由于在直线电机解析模型建立过程中存在假设条件，会产生模型计算的误差，并不适合优化设计的高精确度计算，因此建立基于Kriging模型[26]与EI加点准则的代理模型为后续优化工作提供高精确度的模型基础。

优化过程分为两个阶段，第一阶段，根据3个优化变量以及对应优化目标响应值的样本数据库建立Kriging模型，并对模型进行寻优。第二阶段，通过EI加点准则加入样本点来更新Kriging模型，提高模型精确度，重复第一阶段，直到满足终止条件。具体优化步骤为：

步骤1：根据空间约束条件，在设计范围内对优化变量采取拉丁超立方抽样，选取分布均匀的样本点，通过有限元仿真软件计算样本点的响应值。

步骤2：通过样本点建立Kriging模型。

步骤3：采用多种群遗传算法对Kriging模型进行优化，求解Pareto前沿。

步骤4：计算EI准则表达式，将EI值最大的点作为新的样本点加入到模型中，提高模型在最优解区域的精确度。

步骤5：判断EI值是否达到最大样本点数，满足条件则输出Pareto前沿，否则返回步骤2。

优化流程如图13所示。

4.1"第一阶段优化

建立Kriging模型把系统响应与变量之间的关系通过已知样本数据进行构造，并采用多种群遗传算法进行寻优。

首先，采用拉丁超立方抽样的方法在设计范围内选取初始样本点，抽样维度bound设置为3，样本点数n设置为50。通过有限元仿真软件计算50个样本点的平均推力、推力波动和推力体积比，建立低精确度的Kriging模型，部分样本点如表5所示。Kriging模型通过MATLAB中dace工具箱建立，其回归部分为二次型，随机部分采用高斯函数。

其次，设置多种群遗传算法初始种群数目MP=10。将交叉算子Pc、变异算子Pm作用于种群，两种算子计算过程为：

Pc（g）=Pc（1）+c×frand（MP，1）；

Pm（g）=Pm（1）+m×frand（MP，1）。（27）

式中：初代交叉算子Pc（1）=0.7，初代变异算子Pm（1）=0.001；c、m分别交叉运算和变异算子操作区间，取[0.7，0.9]、[0.01，0.05]；frand为随机数函数，产生[0，1]间随机数的MP×1矩阵。种群P（t）经过选择后，进行交叉和变异运算后得到下一代种群P（t+1），准备下一次遗传操作。若满足算法终止条件，则输出Pareto前沿。

4.2"第二阶段优化

EI加点准则在可能出现最优解的区域选择新样本点，加入新样本点更新Kriging模型，保证了模型的高精确度。EI准则计算的是变量给改进过程带来的期望值，其数学表达式为

式中：Ymin为已知样本点中的最优解；Ymin=min[y（X1），y（X2），…，y（Xn）]；X为设计变量的向量；y（X）为模型预测最优解（第一阶段优化后的Pareto前沿）；s（X）为模型预测误差的标准差；Φ为标准正态分布的累计概率函数；为标准正态分布的概率密度函数。新样本点的y（X）小于Ymin则认为可以改进模型，取新样本点为EI（X）最大时对应的变量如下：

4.3"优化结果分析

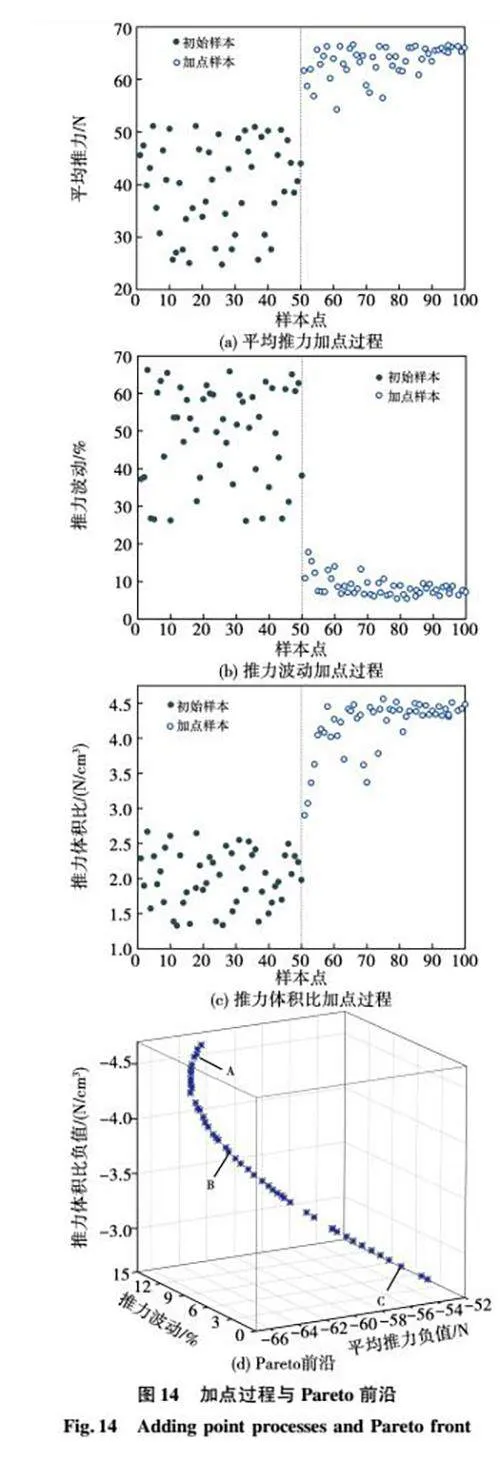
设置加点50次为优化终止条件，优化结束后，加点过程与优化后的Pareto前沿如图14所示，新加样本的响应值明显优于初始样本，3个优化目标使Pareto前沿为三维空间分布。

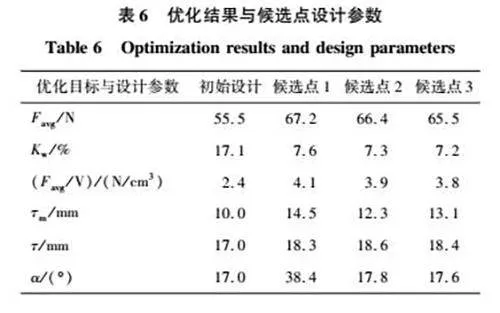
为了得到复合优化目标的最优解，分析Pareto前沿，选择图14（d）中的A、B、C三点作为优化设计解，并与初始设计进行比较。A点推力体积比最大，但推力波动也较大。C点对推力波动有明显抑制效果，但是平均推力和推力体积比较低。B点位于轨迹中心处，对优化设计目标的权衡达到最佳，B点周围的解是最佳的选取区域。在B点附近选择3个候选点，候选点的优化结果和设计参数如表6所示。

5"电磁性能比较与经济性分析

为了证明本文THCPPMLSM结构设计的正确性和实用价值，在有限元仿真软件中进行电磁仿真，对电机的电磁性能和经济性进行分析。以表6中候选点1的设计参数作为THCPPMLSM的优化结果，将HCPPMLSM、DHPMLSM和THCPPMLSM进行比较。为了保证对比结果的可靠性，3种电机参数设置相同，单个永磁体体积相同。

5.1"电磁性能比较

在负载状态下，3种电机的动子受到的磁阻力和电磁推力曲线如图15所示。磁阻力是造成推力波动的主要原因，会影响电机定位精确度，从图15（a）可知，相比于矩形永磁体的HCPPMLSM，永磁体经过设计的DHPMLSM和THCPPMLSM在不同程度上抑制了磁阻力，其中THCPPMLSM在运行过程中受到磁阻力最小。在电磁推力方面，从图15（b）可知，THCPPMLSM的电磁推力波动程度最低，与磁阻力的分析结果相相符合。

进一步对电机性能进行定量分析，对比指标的数值结果如表7所示。综合考察表7数据可知，相比于HCPPMLSM（M1），THCPPMLSM（M3）在平均推力上提高63.1%，磁阻力峰峰值降低92.6%，推力波动降低76.6%，说明梯形Halbach磁极可以大幅降低磁阻力干扰。相比于DHPMLSM（M2），THCPPMLSM（M3）具有更好推力波动抑制效果，并在永磁体利用率上，动子部分耦合永磁体体积为DHPMLSM（M2）的69.5%，推力体积比提高28.1%，说明梯形Halbach交替极在保证电机出力性能良好的同时，永磁体利用率更高。

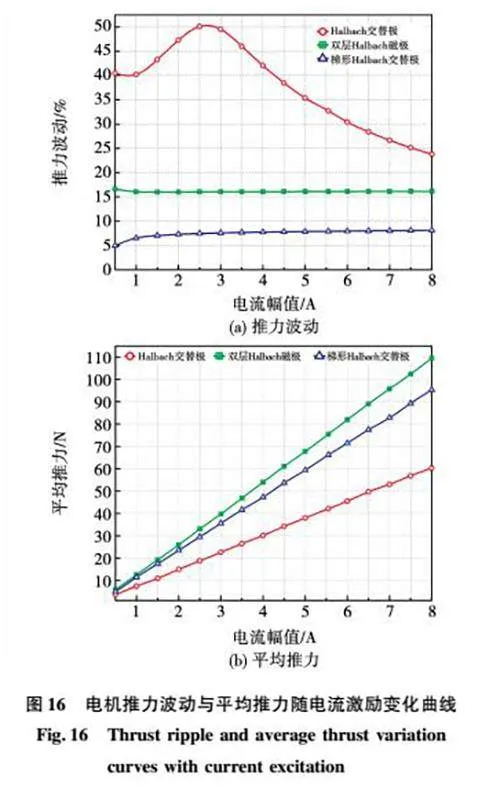
最后，在仿真软件中依次设置0.5～8 A的电流激励，计算不同电流激励情况下3种电机的推力波动和平均推力的定量结果，验证在不同电流激励的工况下PMLSM的适应性。在推力波动方面，如图16（a）所示，HCPPMLSM推力波动最大，并且随电流变化有着较大的不稳定性，而DHPMLSM和THCPPMLSM的推力波动分别稳定在16%和7%左右。推力方面，从图16（b）可知，在THCPPMLSM的动子部分耦合永磁体体积为DHPMLSM的69.5%的情况下，平均推力差距只在14 N以内，并且推力表现优于同等永磁体用量的HCPPMLSM。

5.2"经济性分析

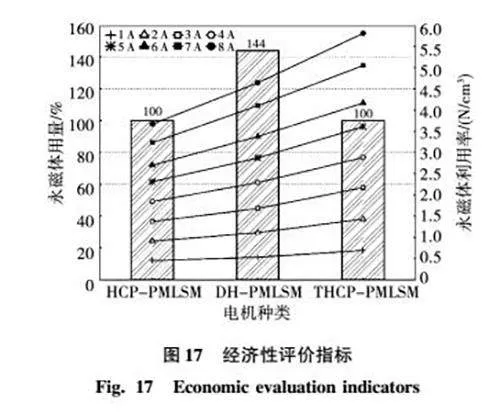
电机的经济性评价指标以一定的永磁体用量为基础，以电机中永磁体的利用率来评价，若永磁体用量越少，且永磁体利用率越高，则表明电机在经济性方面越具有实用价值。

经济性分析的评价指标如图17所示，用柱状图表示永磁体用量，以THCPPMLSM为标准，显示3种电机的永磁体用量的倍率关系。用点线图表示永磁体的利用率，显示电机在1～8 A的电流激励下的永磁体利用率。分析图17可知，DHPMLSM的永磁体用量是两个交替极结构电机的1.44倍，本文提出的THCPPMLSM在永磁体用量上更少；在同等电流条件下，可以看出THCPPMLSM的永磁体利用率更高，通过综合考虑，经济性分析表明本文提出的THCPPMLSM具有更高的实际应用价值。

6"结"论

本文提出梯形Halbach交替极永磁同步直线电机，并对电机的电磁特性进行了分析与优化。针对交替极结构中凸铁极与永磁体磁场不对称问题，提出了永磁体错极排布以优化气隙磁场分布的结构。为了在降低永磁体用量的同时提高电机出力性能，采用了结合EI加点准则的Kriging模型对磁极结构进行了优化。经过对电机磁极结构的分析与研究，得到以下结论：

1）首先，针对电机系统分别在静磁场状态、瞬态空载状态以及负载状态，对比了HCPPMLSM、DHPMLSM和THCPPMLSM这3种电机的电磁性能，并对交替极进行错极排布的优化。经过对比，THCPPMLSM可有效抑制气隙磁场中的5次与9次谐波，拥有更大的永磁体利用率。

2）采用等效磁化强度的方法定性分析了磁极结构对电机性能的影响，结合EI加点准则的Kriging快速计算模型和多种群遗传算法对关键参数进行了优化。优化后，THCPPMLSM的平均推力提升了21.1%，推力体积比提升70.8%，推力波动降低55.6%。

3）相比于同等永磁体用量的HCPPMLSM，THCPPMLSM在不同工况下具有更好的稳定性，推力波动最大可以降低85.9%，平均推力最大可提升51.3%，更适用于高精确度加工场景。相比于DHPMLSM，THCPPMLSM的推力波动降低了55.7%左右，在达到相近的推力水平时，永磁体用量为DHPMLSM的69.5%。

最后通过经济性分析，综合考虑了电机永磁体的用量成本与利用率，相比于HCPPMLSM和DHPMLSM，THCPPMLSM具有更高的实际应用价值。

参 考 文 献：

［1］"卢琴芬， 沈燚明， 叶云岳.永磁直线电动机结构及研究发展综述[J]. 中国电机工程学报， 2019， 39（9）： 2575.

LU Qinfen， SHEN Yiming， YE Yunyue. Development of permanent magnet linear synchronous motors structure and research[J]. Proceedings of the CSEE， 2019， 39（9）： 2575.

［2］"汪旭东， 肖驰， 封海潮. U型永磁开关磁链直线电机特性分析及优化[J]. 电机与控制学报， 2021， 25（2）： 132.

WANG Xudong， XIAO Chi， FENG Haichao.Characteristic analysis and optimization of Utype permanent magnet fluxswitching linear motor[J].Electric Machines and Control，2021，25（2）：132.

［3］"CAO R， JIN Y， ZhANG Z， et al. A new doublesided linear fluxswitching permanent magnet motor with yokeless mover for electromagnetic launch system[J]. IEEE Transactions on Energy Conversion， 2019， 34（2）： 680.

［4］"TAN Q， WANG M， LI L， et al. Pulsating magnetic field of permanent magnet linear synchronous motor and its influence on detent force[J]. IEEE Transactions on Energy Conversion， 2021， 36（2）： 703.

［5］"周游， 石超杰， 曲荣海，等. 磁场调制永磁直线电机拓扑研究综述[J]. 中国电机工程学报， 2021， 41（4）： 1469.

ZHOU You， SHI Chaojie， QU Ronghai， et al. Overview of fluxmodulation linear permanent magnet machines[J]. Proceedings of the CSEE， 2021， 41（4）： 1469.

［6］"樊英， 谭超. 内置式交替极永磁同步电机性能及机理研究[J]. 电工技术学报， 2018， 33（11）： 2414.

FAN Ying， TAN Chao. Analysis of electromagnetic performance and principles in inserted consequentpole permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society， 2018， 33（11）： 2414.

［7］"许孝卓， 孙震， 汪旭东， 等. Halbach交替极永磁同步直线电机特性分析[J]. 电工技术学报， 2019， 34（9）： 1825.

XU Xiaozhuo， SUN Zhen， WANG Xudong， et al. Characteristic of a novel permanent magnet linear synchronous motor with Halbach array consequentpole[J]. Transactions of China Electrotechnical Society， 2019， 34（9）： 1825.

［8］"宗开放， 赵吉文， 宋俊材，等. 基于V型线圈永磁同步直线电机推力波动抑制[J]. 中国电机工程学报， 2019， 39（22）： 6736.

ZONG Kaifang， ZHAO Jiwen， SONG Juncai， et al. Thrust ripple reduction based on Vcoil permanent magnet synchronous linear motors[J]. Proceedings of the CSEE， 2019， 39（22）： 6736.

［9］"LI Y X， ZHU Z Q， THOMAS A S， et al. Novel modular fractional slot permanent magnet machines with redundant teeth[J]. IEEE Transactions on Magnetics， 2019， 55（9）： 1.

［10］"陈浈斐， 汤俊， 马宏忠，等. 星–三角接法的多层绕组分数槽永磁电机谐波磁动势分析[J]. 中国电机工程学报， 2021， 41（17）： 6060.

CHEN Zhenfei， TANG Jun， MA Hongzhong， et al. Harmonic magnetomotive force analysis of multilayerwinding FSCWPM machine with stardelta hybrid connection[J]. Proceedings of the CSEE， 2021， 41（17）： 6060.

［11］"吕刚， 张贤. 不同槽配合格栅型直线感应电机电磁特性研究[J]. 电机与控制学报， 2019， 23（5）： 18.

L Gang， ZHANG Xian. Investigation of electromagnetic characteristics of linear induction motor with laddertype secondary under different slot combination[J]. Electric Machines and Control， 2019， 23（5）： 18.

［12］"兰志勇，谢斌，祝涤非，等. 基于V型三段磁极错位削弱永磁直线电机推力波动的方法[J]. 电工技术学报， 2021， 36（16）： 3474.

LAN Zhiyong， XIE Bin， ZHU Difei， et al. Method for weakening thrust fluctuation of permanent magnet linear motor based on Vshaped threestage magnetic pole misalignment[J].Transactions of China Electrotechnical Society， 2021， 36（16）： 3474.

［13］"彭兵， 李丽萍， 张囡，等. 双V型结构削弱永磁直线电机磁阻力波动方法[J]. 电工技术学报， 2017， 32（22）： 108.

PENG Bing， LI Liping， ZHANG Nan， et al. A method for reducing detent force fluctuation by doubleVshaped structure in permanent magnet linear motor[J].Transactions of China Electrotechnical Society， 2017， 32（22）： 108.

［14］"彭兵， 刘铁法， 张囡，等. 凹型端齿削弱永磁直线电机端部力波动方法[J]. 电工技术学报， 2015， 30（7）： 119.

PENG Bing， LIU Tiefa， ZHANG Nan， et al. A method for reducing the end effect force fluctuation by the concave profile endtooth in permanent magnet linear motors[J]. Transactions of China Electrotechnical Society， 2015， 30（7）： 119.

［15］"彭兵， 张囡， 夏加宽，等. 永磁直线电机端部效应力的解析计算[J]. 中国电机工程学报， 2016， 36（2）： 547.

PENG Bing， ZHANG Nan， XIA Jiakuan， et al. Analytical calculation for end effect forces in permanent magnet linear motors[J]. Proceedings of the CSEE， 2016， 36（2）： 547.

［16］"韩正清， 许金， 芮万智， 等. 高速短初级直线感应电动机等效电路模型及时变参数辨识[J]. 电机与控制学报， 2021， 25（11）： 8.

HAN Zhengqing， XU Jin， RUI Wanzhi， et al.Equivalent circuit model and timevarying parameter identification of high speed short primary linear induction motors[J]. Electric Machines and Control， 2021， 25（11）： 8.

［17］"TAN Q， HUANG X， LI L， et al. Magnetic field analysis and flux barrier design for modular permanent magnet linear synchronous motor[J]. IEEE Transactions on Industrial Electronics， 2020， 67（5）： 3891.

［18］"杨阳， 赵吉文， 宋俊材，等. 基于深度神经网络模型的无铁心永磁同步直线电机结构优化研究[J]. 中国电机工程学报， 2019， 39（20）： 6085.

YANG Yang， ZHAO Jiwen， SONG Juncai， et al. Structural optimization of aircore permanent magnet synchronous linear motors based on deep neural network models[J]. Proceedings of the CSEE， 2019， 39（20）： 6085.

［19］"SONG J， DONG F， ZHAO J， et al. An efficient multiobjective design optimization method for a PMSLM based on an extreme learning machine[J]. IEEE Transactions on Industrial Electronics， 2019， 66（2）： 1001.

［20］"张鲁， 寇宝泉， 赵斌超，等. 新型Halbach次级结构永磁同步直线电机[J]. 电工技术学报， 2013， 28（7）： 39.

ZHANG Lu， KOU Baoquan， ZHAO Binchao， et al. A novel synchronous permanent magnet linear motor with Halbach secondary structure[J].Transactions of China Electrotechnical Society， 2013， 28（7）： 39.

［21］"S P J. Optimal latinhypercube designs for computer experiments[J].Journal of Statistical Planning amp; Inference，1994，1（39）： 95.

［22］"李立毅， 唐勇斌， 刘家曦，等. 多种群遗传算法在无铁心永磁直线同步电机优化设计中的应用[J]. 中国电机工程学报， 2013， 33（15）： 69.

LI Liyi， TANG Yongbin， LIU Jiaxi， et al. Application of the multiple population genetic algorithm in optimum design of aircore permanent magnet linear synchronous motors[J]. Proceedings of the CSEE， 2013， 33（15）： 69.

［23］"ZHANG Y， YANG Z， YU M， et al. Analysis and design of doublesided air core linear servo motor with trapezoidal permanent magnets[J]. IEEE Transactions on Magnetics， 2011， 47（10）： 3236.

［24］"汪伟涛， 赵吉文， 宋俊材，等. 双层反向倾斜线圈永磁同步直线电机的设计与优化[J]. 中国电机工程学报， 2020， 40（3）： 980.

WANG Weitao， ZHAO Jiwen SONG Juncai， et al. Design and optimization of double layer reverse dip coil permanent magnet synchronous linear motors[J]. Proceedings of the CSEE， 2020， 40（3）： 980.

［25］"WANG W， ZHAO J， SONG J， et al. Thrust performance improvement for PMSLM through doublelayer reverse skewed coil and WRFMKH method[J]. IEEE/ASME Transactions on Mechatronics， 2020， 25（6）： 2950.

［26］"黄燕，李露，蒋孝文，等. 基于Kriging和NSGAⅢ算法的汽车交流发电机温度场预测模[J]. 电机与控制学报， 2022， 21（1）： 86.

HUANG Yan， LI Lu，JIANG Xiaowen， et al. Prediction of temperature field for automative generator based on Kriging and NSGAⅢ algorithms[J]. Electric Machines and Control， 2022， 21（1）： 86.

（编辑：刘素菊）

收稿日期： 2022-06-28

基金项目：国家自然科学基金（51867012）

作者简介：缪仲翠（1971—），女，副教授，硕士生导师，研究方向为交流电机先进控制、直线驱动系统方面；

苏"乙（1997—），男，硕士研究生，研究方向为直线电机优化设计及其温度场；

张"磊（1996—），男，硕士研究生，研究方向为直线电机优化设计及其控制；

赵"璇（1998—），女，硕士研究生，研究方向为电动汽车轮毂电机转矩优化分配；

李"燕（1998—），女，硕士研究生，研究方向为五相永磁同步电机容错控制。

通信作者：苏"乙