在初中数学教学中培养学生创新思维的策略探究
2024-06-03黄梅
黄梅
【摘要】随着新课改的逐步落实与推进,教师在开展数学教学时,不仅要重点关注学生掌握基础知识的情况,也要重视培养与锻炼学生的学科素养、综合能力,推动学生全面发展.其中,创新思维是学生应具备的重要思维,可以使学生建立独立思考意识、创新思考能力,全面提高自身的学习效率.文章首先介绍了培养学生创新思维的原则,其次阐述了培养学生创新思维的四种策略,以此助力教师有效开展数学教学活动.
【关键词】初中数学;创新思维;教学策略
引 言
对学生而言,具备一定的思维能力,是有效理解数学知识、理清数学内在关联的重要基础.而创新思维作为较为重要的思维能力之一,需要教师在数学活动中给予落实,切实培养学生具备一定的创新思维能力.基于此,在开展数学教学活动时,教师需要以《义务教育数学课程标准(2022年版)》(下文简称“新课标”)为基准,立足问题情境、合作探究、融合游戏、数学习题为学生构建创新思维发展的空间,促进学生创新思维能力的进步,使学生的核心素养得到强化.
一、在初中数学教学中培养学生创新思維的原则
(一)趣味性原则
在培养学生创新思维的过程中,教师需要理清知识学习、学习动力、学习兴趣三者之间的关系,即要想让学生在数学课堂上处于持续学习的状态,便要让学生具备一定的学习动力,而学习兴趣则是推动学生持续学习的动力源泉.故而,在开展数学教学时,教师需要重视落实趣味性原则,以有趣的教学活动、知识呈现过程等激活学生的学习热情,使学生在兴趣的推动下,全身心参与到数学课堂中.而且,在兴趣的驱动下,学生的思维也会更为活跃,有助于对数学知识的深入思考,使学生的创新思维能力得到良好发展.
(二)开放性原则
在培养学生创新思维时,教学内容的开放程度也会影响学生创新思维的形成.在传统数学课堂中,教学内容多以单一的方式呈现,且教师在设置数学问题时,也大多以有明确结果的问题为主,学生只需要按照教师提供的思路完成思考,便可以获得知识内容.这一过程缺少了学生开放思考的过程,导致学生无法建立思考问题的意识.对此,教师需要遵循开放性原则,在保证教学内容得到全部落实的基础上,让课程呈现方式、设置的思考问题都具备开放性,以此锻炼学生多角度思考的能力,这对学生发展创新思维有积极的促进意义.
(三)引导性原则
在传统数学课堂中,一些教师会采取“灌输式”的教学方式,而在这一过程中,教师缺少了对学生的引导,未注重锻炼学生的自主思考能力,导致学生在后续的学习中,过度依赖教师,无法独立完成对数学知识的有效分析与思考.基于此,在新课标背景下,教师需要调整自身的教学观念,充分把握好引导性原则,让学生在教师的引导范围之外,能够有独立自主的思考空间.这样,当学生再面对数学问题时,教师便可以适当点拨,让学生有充分的自主思考空间,而学生便可以在自主思考中进行尝试,直到得到最终的答案.这时,学生的思维得到发散锻炼,更有助于创新思维能力的进步.
二、在初中数学教学中培养学生创新思维的策略
(一)立足问题情境,培养创新思维意识
问题情境是指以数学问题为主的课堂教学情境.在问题情境中,教师会借助对可视化内容的应用,以及设置适当的数学问题,让学生感受到情境的趣味性,以此调动学生的学习兴趣,使学生做到充分思考.且在情境中,学生的思维会得到有效激活,有助于培养学生的创新思维意识.
以“一元二次方程”一课的教学为例,教师需要带领学生掌握一元二次方程的概念、学习一元二次方程的一般形式及其有关概念.首先,教师以思考题的形式引发学生探索,让学生在问题情境中理解和认识一元二次方程.具体题目为:如图1,有一块长为100厘米、宽为50厘米的长方形纸板,为了制作纸盒,现需要对纸板进行剪裁,即需要裁剪长方形纸板的四个角,每个角裁下一个小正方形.裁剪后的纸板可以折叠为一个无盖的纸盒.已知纸盒底部的面积为3600平方厘米,求裁下的四个小正方形的面积一共是多少.
在解决这一问题时,教师可以问题的形式引导学生思考:“如果要求出正方形的边长,其内在思考逻辑是什么?”这时,学生便需要思考正方形的边长与哪些条件有关,如与长方形的边长相关,也与纸盒底部的边长相关.再进一步思考,学生便会发现,求出纸盒的面积需要用到长方形的长和宽与正方形的边长.基于此,学生可以尝试列出方程:设裁下的小正方形的边长为x厘米,则纸盒底部的长度为(100-2x)厘米,宽度为(50-2x)厘米.根据纸盒底部的面积,可以得到对应的方程:(100-2x)(50-2x)=3600,再进一步整理为x2-75x+350=0,通过计算即可得出本题答案.接着,教师可继续以思考问题帮助学生巩固列一元二次方程的知识.
在上述教学过程中,教师以设置问题情境的方式,组织学生思考列一元二次方程的知识,并以思考问题的形式,引导学生的思路,使学生借助教师的适当点拨,完成对一元二次方程知识的思考,进而达到引导学生思考、强化学生创新思维的目的.
(二)立足合作探究,促进创新思维发展
合作探究是指将学生按照一定的原则分组,由教师根据教学内容布置适当的探究任务,学生合作完成探究过程的一种教学方式.对学生而言,合作探究不仅是从知识层面广泛思考知识点,更重要的是从思想层面,锻炼自身的发散思维,并在此基础上实现创新思维的进步.故而,教师需要有效组织学生进行合作探究,促进学生创新思维的发展.

根据上面叙述的过程,教师以合作探究的方式,组织学生交流有关实际问题与一元二次方程的知识内容,以此锻炼学生的探究能力,让学生的创新思维在共同探索中得到进步与发展.
(三)立足融合游戏,提供创新思维空间
在以往的数学课堂中,教师较少会在课堂中融合游戏,多数教师会认为这样影响课堂纪律、干扰正常教学.但是,经过一定时间的教学实践可以发现,游戏与课堂教学的有效融合,可以提高课堂教学效率.对此,在培养学生创新思维时,教师可以采取融合游戏的方式,在数学课堂上为学生提供创新思维空间.
以“图形的旋转”一课教学为例,教师需要组织学生完成对旋转定义、性质、应用等内容的探索,并且可以欣赏旋转图案,体会旋转变化的魅力.基于此,在讲授这部分知识时,为了培养学生的创新思维,教师需要以游戏的形式为学生提供创新思维空间,即让学生有独立思考、勇闯游戏关卡的意识.首先,教师可以将整堂课程内容设置为闯关游戏的形式,学生每完成对一个知识点的学习,便成功闯过一关.在最后的总关卡中,教師可以课程知识归纳或者习题检测的方式,对学生进行考核.首先,在第一个关卡中,学生需要观察动画,总结旋转概念.教师展示了两种不同的事物让学生观察,即圆形钟表与风车.在钟表指针、风车旋转的过程中,学生需要仔细观察其中变化的内容与未发生变化的内容.对此,学生可以发现,不论是钟表的指针还是风车,其在旋转时,中心的固定点不发生移动,且有具体旋转方向,同时学生发现,当旋转的物体停止旋转时,其位置发生了变化.对此,在教师的点拨下,学生可以快速地总结出旋转的对应概念.这时,学生成功闯过第一关.接着,教师需要为学生布置第二关、第三关,直至学生完成对旋转知识的综合掌握,可以用旋转知识解决简单的问题.
至此,教师便借助对游戏形式的运用,组织学生完成了对旋转知识的思考与掌握,且在游戏中,教师以学生为主,为学生提供了具体的思考空间,让学生的创新思维得到了成长.
(四)立足数学习题,锻炼创新思维能力
数学习题是学生理解数学知识、锻炼数学能力的重要途径.在新课标背景下,教师需要重视提升数学习题的质量,以此使学生用较少的习题掌握较多的数学知识.通过设置数学习题的方式,教师可以组织学生进行自主练习,让学生根据已掌握的知识内容,完成对习题的有效思考,形成举一反三的思维模式,进而达到锻炼创新思维能力的目的.
以“点和圆、直线和圆的位置关系”这一课教学为例,教师可以借助布置课后习题的方式锻炼学生的创新思维,让学生在习题中强化举一反三的能力.在题目的选择上,教师应保证题目难度呈阶梯式上升.首先,以简单的题目切入,如:已知☉O的半径是6,点O到直线l的距离为5,则直线l与☉O的位置关系是( );在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以点C为圆心,r为半径作圆,若☉C与直线AB相切,则r的值为( ).对于这一类简单的题目,学生运用基础知识并结合简单的计算,便可以得出相应的结果.其次,以有难度的题目实现深度思考.如图3,AB是☉O的直径,CD是☉O中任意一条弦,求证:AB≥CD.在解决这一问题时,学生需要用到半径相等的知识,再具体思考如何建立AB与CD之间的关系,便可以做到对该问题的有效解决.对此,学生在解题时,将点C、点D分别与圆心O相连,这时OC与OD便是圆的半径,即OC=OD=OA=OB,再根据三角形两边之和大于第三边的知识,学生便可以得到OC+OD≥CD,即OA+OB≥CD,则AB≥CD.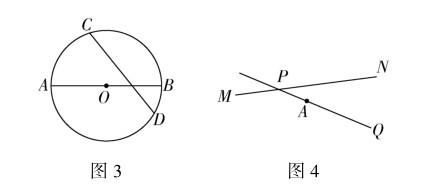
再如,根据图4所示,公路MN与公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.假设当拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否受到噪音影响?如果不受影响,请说明理由;如果受影响,且拖拉机的速度为18km/h,那么学校受影响的时间是多少秒?
在以习题为主的教学中,学生以习题的方式锻炼举一反三的思维,做到在面对各种形式的数学问题时,都能够找到最根本的解题思路,这样,学生便可以在掌握基础知识的同时,有效锻炼自己的创新思维能力.
结 语
综上,在开展以培养学生创新思维能力为主的数学教学工作时,教师应以新课标为依据,充分遵循趣味性原则、开放性原则、引导性原则,从思想上引导学生建立兴趣驱动学习的意识、多角度思考知识的意识、独立自主学习的意识,最终实现培养创新思维能力的目的.在运用教学策略时,教师需要从问题情境、合作探究、融合游戏、数学习题四个角度入手,呈现多样化的教学场景,以此培养创新思维意识、促进创新思维发展、锻炼创新思维能力,推动学生的创新思维得到全方位发展.
【参考文献】
[1]黄金金.在初中数学教学中如何培养学生从失败中寻找创新的能力[J].数理天地(初中版),2023(21):89-91.
[2]赵雅倩.在初中数学教学中培养学生创新思维能力的策略研究[J].天天爱科学(教学研究),2023(9):84-85.
[3]刘颗星.初中数学教学中培养学生创新能力探究[J].智力,2023(13):111-114.
[4]张孝伟.浅议初中数学教学中如何培养学生的数学思维能力[J].当代家庭教育,2023(4):143-145.
[5]李伟强.探讨初中数学教学中创新思维的培养[J].中学课程辅导,2023(5):33-35.
